Avstånd till linje
Hej,
har fastnat på denna uppgift;
Vilken punkt på linjen L : är närmast punkten P=(-1,1,-1)? Vad är avståndet mellan punkten P och linjen L?
Lösningsförslaget säger detta;

Jag blir dock lite förvirrad vad dom menar vad som är vad. Har ritat upp följande och undrar om jag tänker rätt;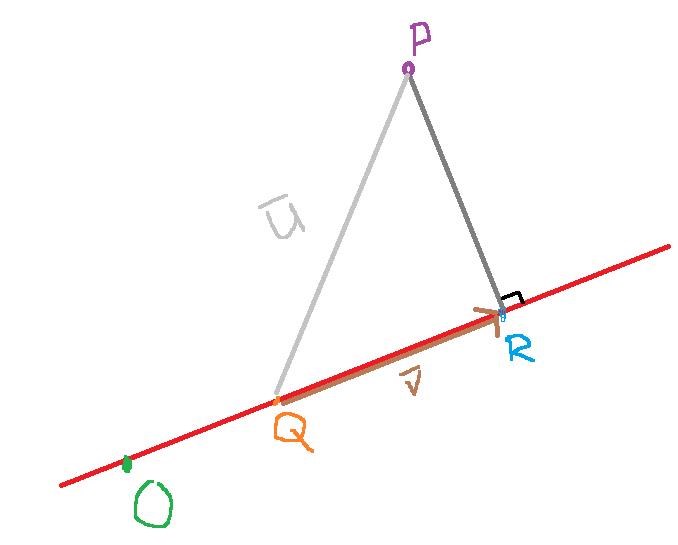 Det jag fastnar på är att det står att man ska beräkna och de då skriver
Det jag fastnar på är att det står att man ska beräkna och de då skriver
men jag tänker att (1,-2,1) är punkten Q.
Ja, (1,-2,1) är ju koordinatetna för punkten Q men de beräknar vektorn OR = OQ+QR där OQ är vektorn (1,-2,1) eftersom det är en ortsvektor för punkten Q om jag har förstått det rätt
är inte vektorn från Q till R som i din bild, utan bara en vektor som beskriver ett steg i linjens riktning. Vektorn från Q till R är det som lösningen kallar , alltså den komponent av u som är parallell med v.
Sedan har du helt rätt i att de använder punkten Q för att beräkna . Eftersom vi nu har en vektor för att gå från Q till R, går vi först till Q och sen längs vektorn som leder därifrån till R:
Jag har gjort ett alternativ, som inte använder sig av ortsvektorer, som i ditt lösningsförslag.
Jag tycker det går lika bra (eller bättre) med Pythagoras. Förhoppningsvis lite mindre förvirrande.
Sökt: Avståndet s.
Betrakta figuren nedan:

Vektorn .
Vektorn är :s ortogonala projektion på linjen L.
Med projektionsformeln: ,
där är linjens normerade riktningsvektor. Uträknat får vi
.
Pythagoras: , varav
, dvs , och vi är klara.
Det går också att lösa det som ett minimeringsproblem.
Låt vara avståndet mellan linjen och punkten för varje värde på parametern . Den sökta punkten på linjen fås då genom att minimera:




