Avståndet som han springer

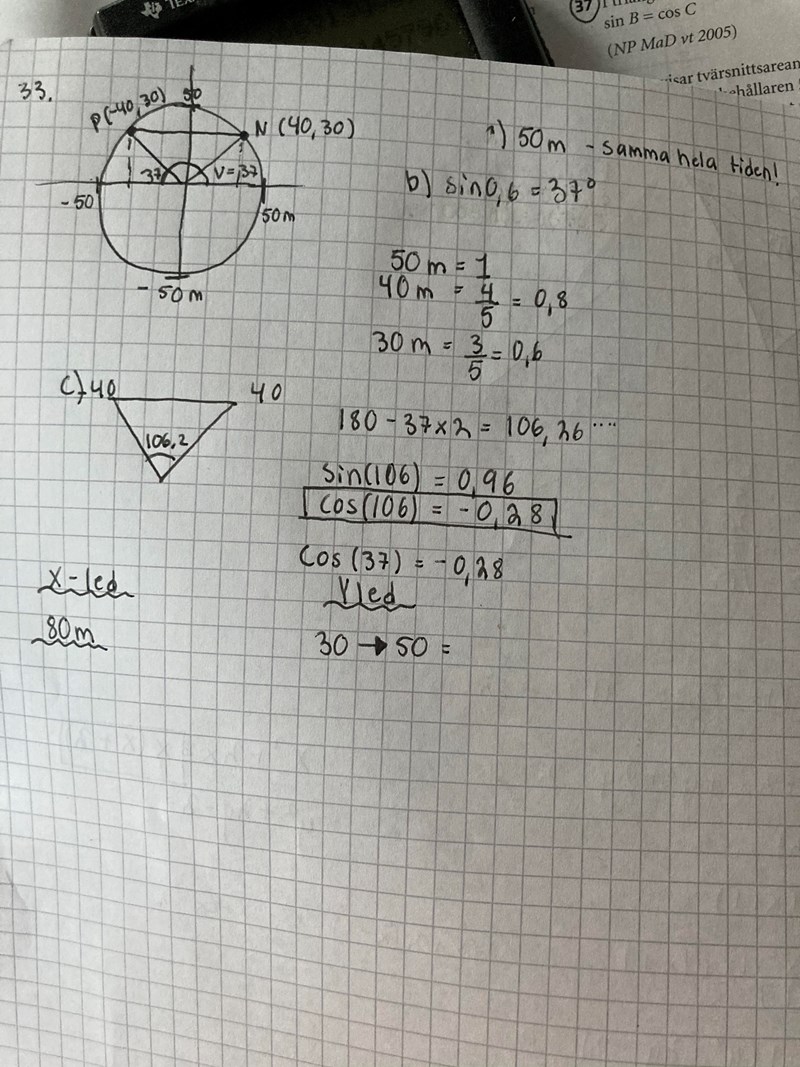Hej! Jag har löst a och b. Men vet inte riktigt hur man ska tänka kring c. För tänkte jag att jag skulle ta förflyttning i x led och förflyttning i y led att behandla det som två katetrer och behandla avståndet som en hypotenusa. Men i och med att han springer RUNT dvs inte en räkstäcka som en hypotenusa är, så vet jag inte riktigt hur jag ska komma vidare:)

Han springer på en cirkel med radien 50 m. Vet du hur man beräknar båglängden, när man vet radien och kan ta reda på vinkeln?

På Mattecentrum.se finns en formelsamling där finns formeln för hur du räknar ut cirkelbågen. Se länk nedan:

https://www.formelsamlingen.se/alla-amnen/matematik/geometri-i/cirkelsektor

Radien blir precis som du säger 50 m. Och vinkeln får jag till 106 ungefär. Men har inte gått igenom hur man räknar en cirkelbåge. Men får 106/360* 2*pi* 50. Det stämmer med facit också tack så mycket! Finns det några andra sätt att lösa uppgiften?

Om det finns något annat sätt så är det nog krångligare.

Formeln för båglängd är egentligen ganska självklar när man väl förstår den.

Hela omkretsen är $2\pi r$ .

Om öppningsvinkeln vid medelpunkten är $v$ grader så är ju båglängden bara en andel av hela omkretsen. Denna andel motsvarar öpnningsvinkelns andel av $360^{\circ}$ , dvs $\frac{v}{360^{\circ}}$ .

Det ger oss att båglängden är $\frac{v}{360^{\circ}}\cdot2\pi r$

========

En kommentar: Du tänkte rätt men blandade ihop vinkel med sinusvärde här:

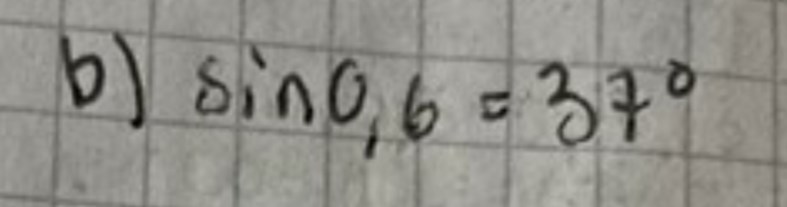
Drt ska stå $\sin(v)=0,6$ , vilket ger $v\approx 36,9^{\circ}$ och $v\approx143,1^{\circ}$

Svara

Visa senaste svar