Avståndsformel - Vilka är koordinaterna?
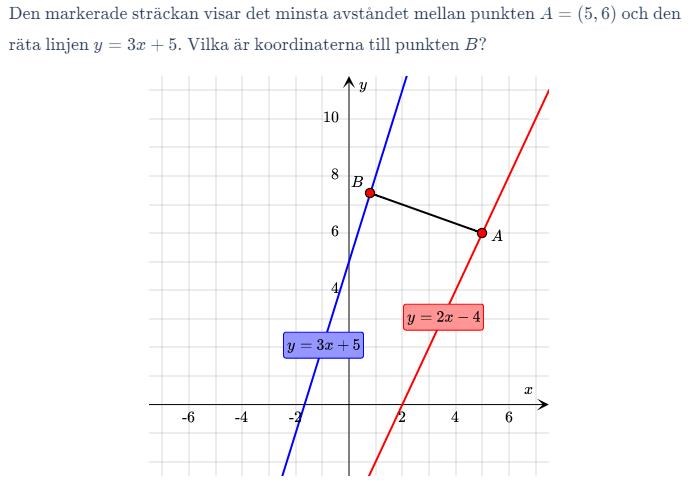
Har fastnat med denna uppgiften.
Försökt med att B = (x , 3x+5) och A = (5, 6) och sedan tagit fram uttryckt för avståndet med hjälp av avståndsformeln.
Får att avståndet mellan punkterna d = och vet inte hur jag ska fortsätta.
Avståndet mellan punkten och linjen är som minst när rotuttrycket är som minst, eller hur? Då är även uttrycket under rottecknet minst. Vet du hur du skall göra för att ta reda på det minsta värdet för uttrycket 10x2-10x+25?
symmetrilinjen är =
stoppar in det i funtionen
förstår inte hur jag ska fortsätta.
Vad är det man frågar efter? Vad är det du har räknat ut?
shemeren skrev:symmetrilinjen är =
stoppar in det i funtionen
förstår inte hur jag ska fortsätta.
Att använda avståndsformeln är rätt, men du har inte fått fram rätt uttryck.
När du har det så får du rätt värde på x, och värdet på y kan du lätt räkna ut, och sedan är du klar. Det faktiska avståndet har de inte frågat efter.
så jag har alltså att minsta värdet på x är 0.5
B = (0.5 ; 6.5)
Har jag tänkt rätt? Har inget facit och ser inte ut som att punkten B i bilden ligger på dessa koordinater.
Löste det. Hade räknat fel med avtåndsformeln.
det faktiska
tack för hjälpen
Alternativt inser man att linjen mellan och måste vara vinkelrät mot linjen .
Med hjälp av enpunktsformeln fås då:
Beräkna sedan skärningen mellan linjerna:
...
tomast80 skrev:Alternativt inser man att linjen mellan och måste vara vinkelrät mot linjen .
Med hjälp av enpunktsformeln fås då:
Beräkna sedan skärningen mellan linjerna:
...
intressant lösning




