Bas för kolonnrum
När man ska få fram en bas för värderummet till en matris, spelar det då roll om man utför elementära rad- eller kolonnoperationer? Eller ger rangsatsen att detta är helt ekvivalent?
Om man bara bryr sig om dimensionen, alltså antalet basvektorer, så kan det inte spelar någon roll vad man gör:
- Man kan jobba med radoperationer (som ju bevarar radrummet och i slutändan ger dig en bas för radrummet).
- Man kan jobba med kolumnoperationer (vilket bevarar kolumnrummet aka värderummet, och därmed i slutändan ger en bas för kolumnrummet).
Anledningen till att detta fungerar är precis som du är inne på att
Men - det gäller inte nödvändigtvis att
inte ens om är kvadratisk (om inte vore kvadratisk skulle det ju vara helt kört :P ). Så om du vill ha en faktisk bas för värderummet är det säkrast att hålla sig till kolumnoperationer.
Tips: Prova gärna som övning att konstruera ett par olika exempel på -matriser där man lyckas respektive misslyckas med att få en bas för kolumnrummet genom att utföra radoperationer.
oggih skrev:Om man bara bryr sig om dimensionen, alltså antalet basvektorer, så kan det inte spelar någon roll vad man gör:
- Man kan jobba med radoperationer (som ju bevarar radrummet och i slutändan ger dig en bas för radrummet).
- Man kan jobba med kolumnoperationer (vilket bevarar kolumnrummet aka värderummet, och därmed i slutändan ger en bas för kolumnrummet).
Anledningen till att detta fungerar är precis som du är inne på att
Men - det gäller inte nödvändigtvis att
inte ens om är kvadratisk (om inte vore kvadratisk skulle det ju vara helt kört :P ). Så om du vill ha en faktisk bas för värderummet är det säkrast att hålla sig till kolumnoperationer.
Tips: Prova gärna som övning att konstruera ett par olika exempel på -matriser där man lyckas respektive misslyckas med att få en bas för kolumnrummet genom att utföra radoperationer.
Ok, tack för svar. Men jag vet inte riktigt om min kursbok (Linjär algebra, Sparr) håller med här. Den har ett exempel där vi en matris . Uppgiften är att bestämma baser för noll- och kolonnrum för A. När det kommer till kolonnrummet används radoperationer för att gaussa ner matrisen till . Eftersom de två första kolonnerna är pivotkolonner gäller att och (de två första kolonnerna i den ursprungliga A-matrisen) är en bas för kolonnrummet till A. Men är inte detta en legitim metod?
Jag hade gjort så här:
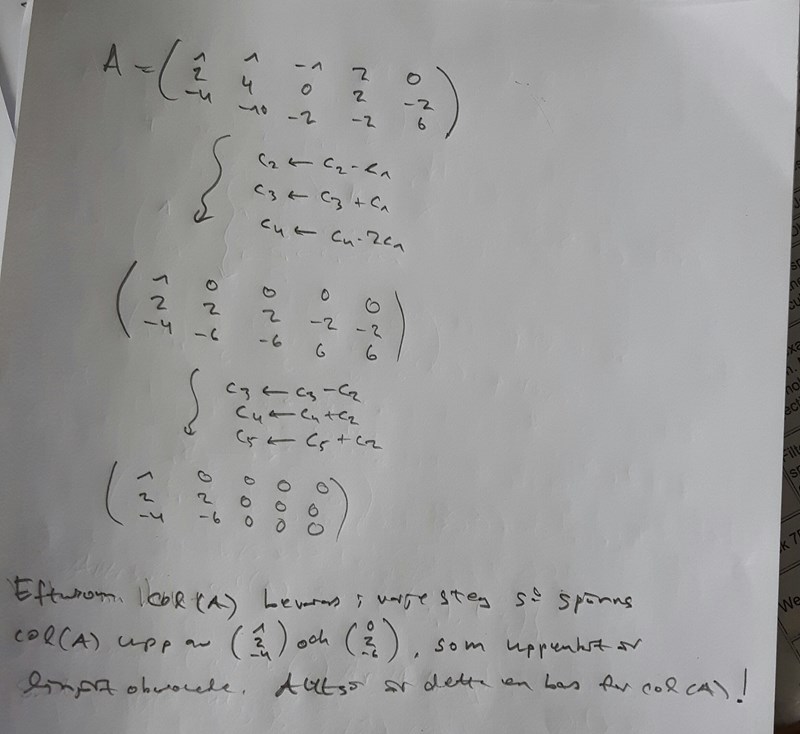
Men det Sparr gör är inte fel (men däremot lite en omväg kanske?). Som jag förstår det så använder han först radoperationer för att konstatera att radrummet (och således även kolumnrummet) har dimensionen 2. Alltså räcker det att bara leta upp två linjärt oberoende element i kolumnrummet, och så är saken biff!
Exempelvis är det lätt att se att kolumn 1 och kolumn 2 är icke-parallella, så de skulle fungera som en bas (men man skulle lika gärna kunna ta exempelvis kolumn 3 och 5).
Med min metod får jag ut en bas direkt efter att ha utfört kolumnoperationerna, så personligen tycker jag det känns mer effektivt och naturligt. Men Sparrs metod kanske lämpar sig bättre för datorberäkningar eller har några andra fördelar!
Edit: Det är möjligt att det är något särskilt med kolumnerna 1 och 2 kopplat till det här med pivotkolumnerna som gör att man kan se att de är linjärt oberoende utan att tänka efter, men det är mer än vad jag begriper mig på. Någon som har (numerisk) linalg mer färskt i huvudet har kanske bättre koll?!
oggih skrev:Jag hade gjort så här:
Men det Sparr gör är inte fel (men däremot lite en omväg kanske?). Som jag förstår det så använder han först radoperationer för att konstatera att radrummet (och således även kolumnrummet) har dimensionen 2. Alltså räcker det att bara leta upp två linjärt oberoende element i kolumnrummet, och så är saken biff!
Exempelvis är det lätt att se att kolumn 1 och kolumn 2 är icke-parallella, så de skulle fungera som en bas (men man skulle lika gärna kunna ta exempelvis kolumn 3 och 5).
Edit: Det är möjligt att det är något särskilt med kolumnerna 1 och 2 kopplat till det här med pivotkolumnerna som gör att man kan se att de är linjärt oberoende utan att tänka efter, men det är mer än vad jag begriper mig på. Någon som har numerisk linalg mer färskt i huvudet har kanske bättre koll?!
Ok, så både (1,2-4) och (0,2,-6) samt (1,2-4) och (1,4,-10) är en legitim bas för kolonnrummet till A? Hur kan man egentligen försäkra sig att de spänner upp samma rum?
I just detta fall kan vi observera att (1,4,-10)=(0,2,-6)+(1,2-4), och från detta direkt dra slutsatsen (hur?) att de båda spannen är lika med varandra.
Men mer allmänt så är det liksom "inbyggt" i metoderna som Sparr respektive jag använde att det man får ut är en bas för col(A). (Säg till om du inte är helt övertygad om någon av metoderna, så försöker jag/någon annan förklara bättre!) Speciellt innebär detta att de resulterande baserna har samma spann, nämligen just col(A).


