Basbyte

Jag tror du måste visa hela uppgiften. Det där var lite svårt att följa.

du ska vara kryssa mot linjens riktning vilken är känd.

Just det jag glömde infoga självaste uppgiften... (uppgift a) ):

oneplusone2 skrev:

du ska vara kryssa mot linjens riktning vilken är känd.

Vad menas med "kryssa mot linjens riktning"  om jag får fråga?

Om du vill kan du ansätta $\hat{\mathbf{e}}_2=(x,y,z)$

Du har då tre ekvationer

$\hat{\mathbf{e}}_1\cdot \hat{\mathbf{e}}_2=0\iff x+y-z=0$

$\hat{\mathbf{e}}_2\cdot(2,1,0)=0\iff 2x+y=0$

$||\hat{\mathbf{e}}_2||=1\iff x^2+y^2+z^2=1$

Om du istället vill vara mer geometrisk kan du se det som att $\hat{\mathbf{e}}_2$ ska ligga i planet vars normal är (2,1,0) och t.ex. ansätta den skalära trippelprodukten vars determinant ska vara +1 för ONH.

Tack! Jag får däremot inte en ortonormerad vektor efter att ha löst ut x, y och z om jag använder ekvationssystemet du tipsat om:

y = -2x ger efter insättning i ekv. nr 1 att x = -z vilket efter insättning i ekv. nr 3 ger att:

 $5x^2 + z^2 = 1 = 6z^2 \Rightarrow z =\pm \frac{1}{\sqrt{6}}$

Detta ger dock inte en ortonormerad bas. Vart blir det fel?

Jag vet ju inte var det blir fel eftersom du inte visar hur du tänkt göra sedan.

Men om vi godtyckligt väljer $z=\frac{1}{\sqrt 6}$ så blir $y=-2z=-\frac{2}{\sqrt 6}$ och $x=-y-z=\frac{1}{\sqrt 6}$. Alltså är $\mathbf{\hat{e}}_2=\frac{1}{\sqrt{6}}(1,-2,-1)$

vidare gäller

$\mathbf{\hat{e}}_3=\mathbf{\hat{e}}_1 \times \mathbf{\hat{e}}_2$

Tack, jag fick fram tre basvektorer som verkar rimliga. Skall det inte vara ê3 = ê2 x ê1 om basen skall vara positivt orienterad?

Är e_z = e_y x e_x om e_x, e_y, e_z är positivt orienterad?

Ja.

Om $\mathbf{e}_x=(1,0,0)$, $\mathbf{e}_y=(0,1,0)$ och $\mathbf{e}_z=(0,0,1)$ så är

$\mathbf{e}_y\times \mathbf{e}_x=(0,1,0)\times (1,0,0)=(0,0,-1)=-\mathbf{e}_z$

Ordningen ($\mathbf{e}_y,\mathbf{e}_x,\mathbf{e}_z$) är alltså inte positivt orienterad.

Däremot är ordningen ($\mathbf{e}_z,\mathbf{e}_x,\mathbf{e}_y$) positivt orienterad eftersom

$\mathbf{e}_z\times \mathbf{e}_x=(0,0,1)\times (1,0,0)=\mathbf{e}_y$

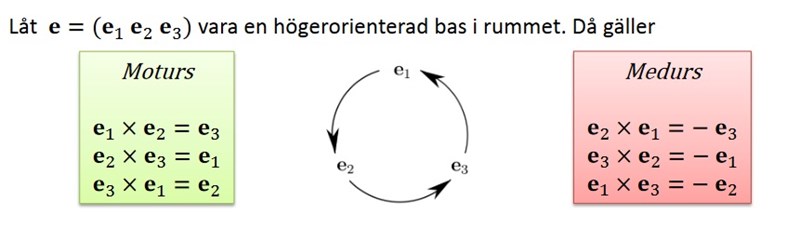
När basvektorerna inte är enhetsvektorer kan man fortfarande säga att en uppräkningsordning är positivt orienterad om vektorerna i ordning förhåller sig som tummen, pekfingret och långfingret på höger hand (högerhandsregeln).

Tack så mycket för din tid och hjälp, då förstår jag!