Basbyte och egenvektorer
Varje gång att jag läser faciten förlorar jag allt vilja att fortsätta leva för dagen.
Såhär:
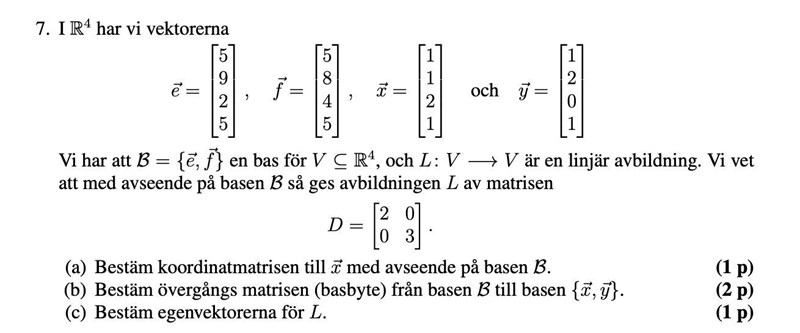
a) varför kallar dem "koordinat matris" en konfiguration 2x1: [-3/5, 4/5]^T ? Varför skriver dem inte isf [{-3/5, 0}, {0, 4/5}]^T
b) efter mycket svett och bearbetning av min basbytesmatris oro, bestämde jag att frågan var att overgången till {x,y} var hur man uttrycker {e,f} i {x,y}, alltså en skalering av {e,f}, och fick [(1,2),(4,3)]^T
c) denna fråga förståd jag total snett däremot. Varför egenvektorer blir {e,f}?
a) Koordinatmatris är ett lite förvirrande uttryck, det är en vektor av koordinater och brukar kallas koordinatvektor
c) Avbildningsmatrisens kolonner är avbildningarna av respektive basvektor. Eftersom första kolonnen är [2,0]^T avbildas e på 2e. Motsvarande avbildas f på 3f. Alltså är e och f egenvektorer för avbildningen (eftersom de avbildas på multiplar av sig själva)
Men harald, gäller inte detta när vi har diagonaliserat? Innan diagonaliseringen, ... ... oh... ok jag måste kanske fundera på det. Ok sluta skriva samtidigt som jag fortfarande tänker. Som nu.
Tack!


