Basbyte orientering (Linjär algebra)

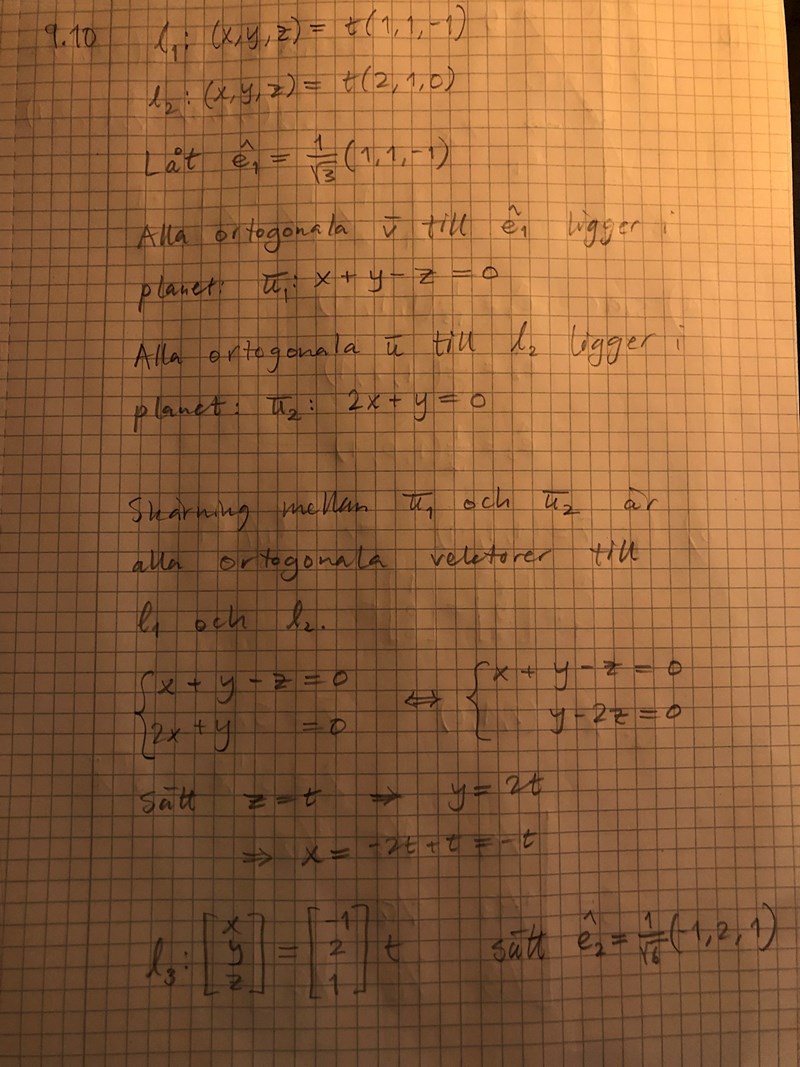
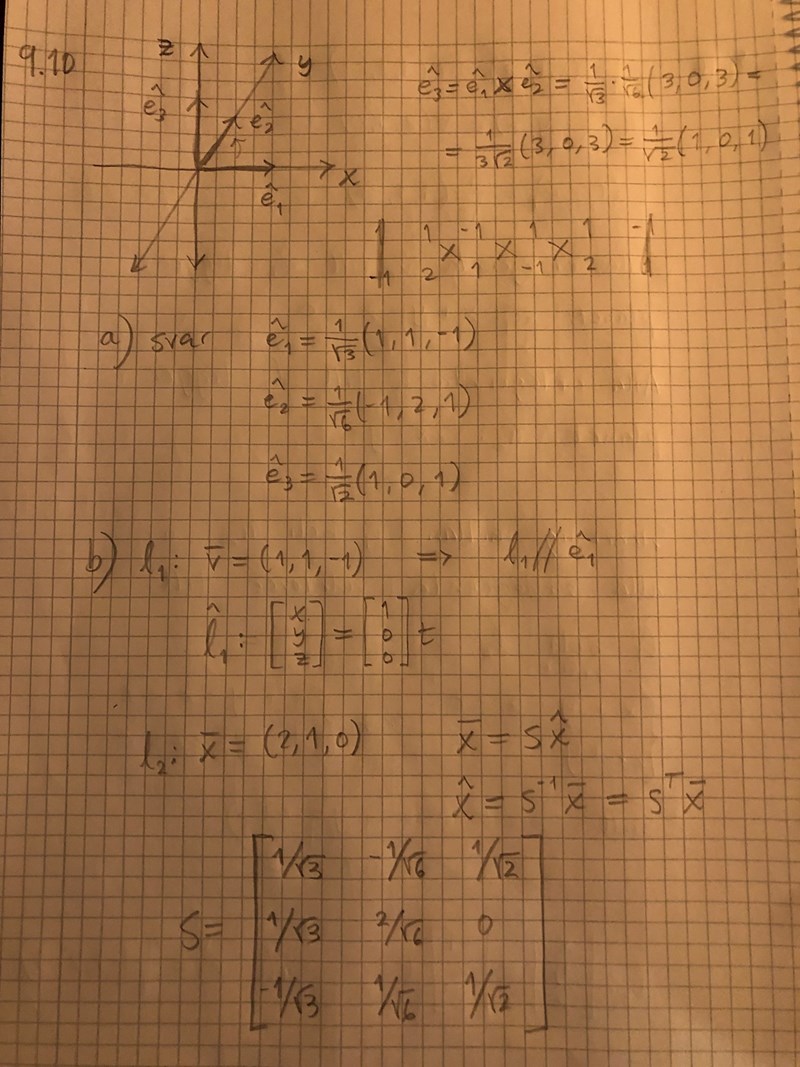
Lång uträkning så ska försöka sammanfatta i ord också. 

Jag sätter direkt att ehatt_1 är riktningsvektorn för linjen L_1. Sen behöver jag en vektor ehatt_2 som är ortogonal mot linjen L_2 och samtidigt mot ehatt_1. Jag tänker mig att ehatt_1 har ett plan av ortogonala vektorer i origo och tar fram en ekvation för planet genom att ehatt_1 är normalvektor. Likaså för L_2. Korsningen mellan dessa två ekvationer är de vektorer som är ortogonala mot båda, så jag löser systemet och får fram en linje L_3. Därefter kan jag sätta ehatt_2 till riktningsvektorn. 

Sen ska jag ta fram ehatt_3 och gör det med hjälp av kryssprodukten, och jag misstänker att det är här det blir fel. Jag tänker mig att jag tittar ner från ehatt_3 på xy-planet med de nya baserna. Då ser jag ehatt_1 som pekar ut mot höger längs x-axeln och ehatt_2 som pekar rakt upp längs y-axeln. För positiv orientering ska jag alltså ta ehatt_1 x ehatt_2 i den ordningen för att ehatt_3 ska peka rätt. Men här måste jag tänka fel, eller?

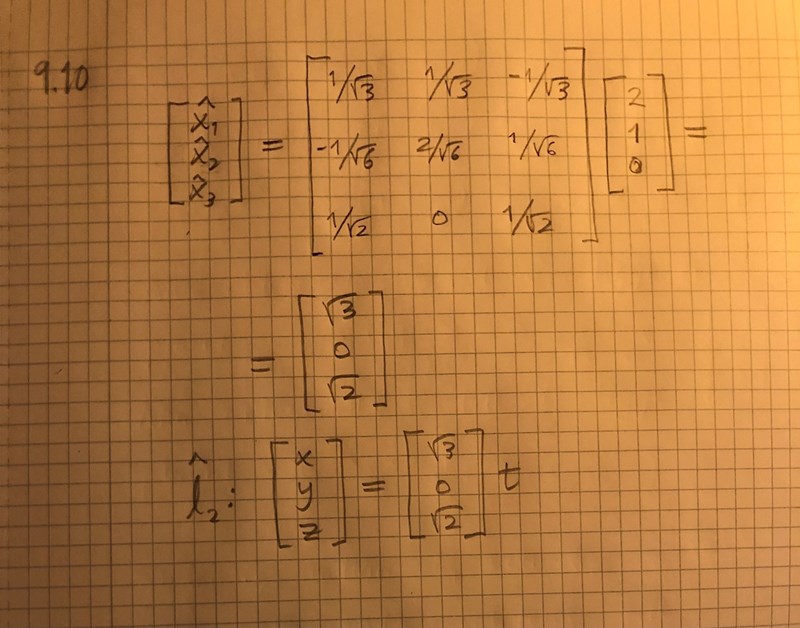
I b) tar jag fram linjerna på parameterform. L_1 blir rätt och L_2 får rätt koefficienter, men fel tecken på z-komponenten. 

Allt blir rätt utom ett minustecken. Vad gör jag för fel? Hur ska jag tänka här?