Bästa skottläget

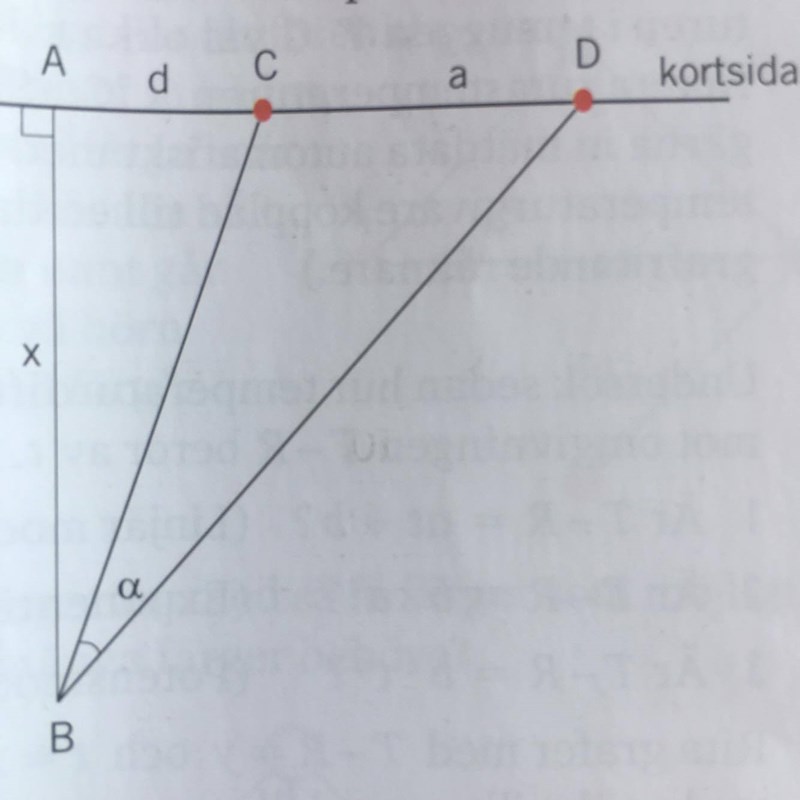
Uppgift: En fotbollsspelare springer längs en linje AB, vinkelrät mot planens kortsida. När har spelaren det bästa skottläget, dvs när ser han målet under den största synvinkeln a?

Ta reda på avståndet a mellan målstolparna C och D och undersök situationen för några olika val av d.

Har kollat på detta svar: http://www.matematik.lu.se/query/answers/q200102.php#20010219154259

Där presenterar dem tan u = a / x samt tan (u+v) = (a + b) / x och därifrån får fram att tan v = tan ((u+v) -u) = (tan(u+v) - tan u) / (1+tan u tan (u+v)) = (b/x) / ((a+(a+b))/x^2) = bx /(x^2+a (a + b))  f(x)

Jag förstår att tan u = a / x samt tan (u+v)=(a+b)/x och även att tan v = tan ((u+v)-u) men inte fortsättningen...

Tacksam för hjälp!