Area och geometri
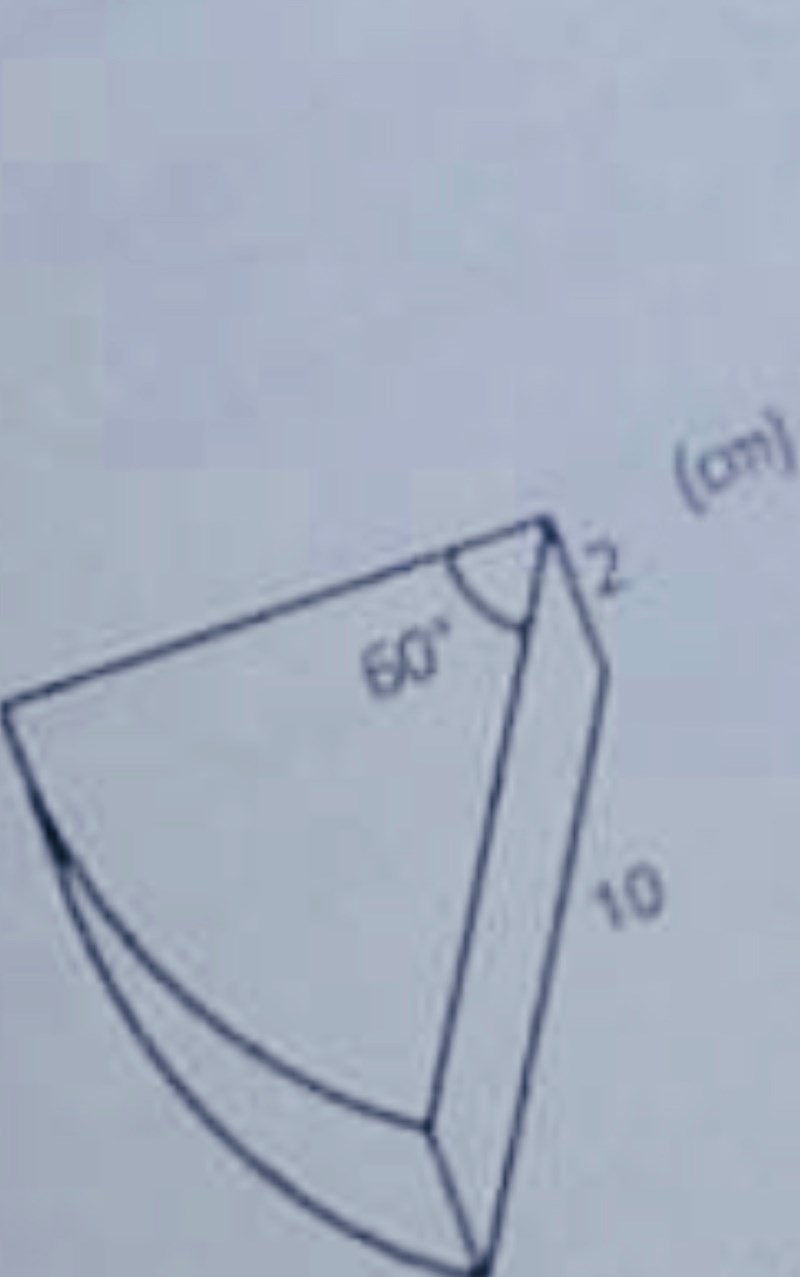Jag har löst uppgiften men vet inte om lösningen är rätt, frågan lyder beräkna begränsningsytan.
min lösning : cirkel sektorn1 : 60/360*5*5=13cm2
sen 13*2 eftersom att det finns 2 st sådana cirkel sektor.
Alltså 26cm^2
sedan finns det 2 st rektanglar där arean av de är 10*2=20 sedan 20*2 = 40
Sedan 1 sid där arean även är 20cm^2
lägger man ihop detta blir det : 40+26+20=86cm^2
är svaret korrekt?
Nej.
Tänk att det är 1/6 av en runt ost med diameter 20 cm.
Varifrån kommer uppgiften?
Hittade uppgiften från gammla pluggakuten men förstod dock inte förklaringen till frågan.
Uppgiften har jag hittat från gammla pluggakuten men förstod dock inte lösningen. Ska man addera cirkelbågarna så svaret blir rätt?
Hehsjsks skrev :Uppgiften har jag hittat från gammla pluggakuten men förstod dock inte lösningen. Ska man addera cirkelbågarna så svaret blir rätt?
Var på gamla pluggakuten hittade du den?
Kopiera in webbadressen här.
---------
Begränsningsytan består av 5 delar:
2 st cirkelsektorer.
2 st raka rektanglar.
1 st böjd rektangel.
Är det korrekta svaret 100cm^2
Hehsjsks skrev :Är det korrekta svaret 100cm^2
Nej det stämmer inte.
Det korrekta svaret är .
Om du visar hur du har räknat så kan vi hjälpa dig att hitta felet.
Det finns 5 sidor.
2 st i mitten o nedredelen
2 st vid sidorna
1 runt den i mitten.
Det låter krångligt.
De 2 st i mitten beräknar jag genom att ta (60/360*r^2)*2 vilket är ungefär 66cm^2
de 2 sidorna beräknas genom att ta (10*2)*2=20cm^2
den sista och som är runt den i mitten beräknas genom att ta 5*2 ... Krångligggtttt :((((
Ska man addera cirkelbågens längd också ??
Du glömmer pi lite här och där.
Har löst om frågan men vet ej om svaret är korrekt :
1) Arean för cirkel sektorn : 60/360*10^2*3,14=52cm^2
52*2 för vi har 2 st cirkel sektorer=104cm^2
2) ( 2*10)*2=40cm^2
3) vi måste ta reda på cirkel bågens längd
då tar man 60/360*20*3,14=10,5
Arean blir 10,5*2=21cm^2
totala begränsningsarean blir 104+40+21=165cm^2
Tänker jag rätt? Är svaret korrekt ??
Du tänker rätt och ditt svar är korrekt.
Och din uppställning är snygg!
Hehsjsks skrev :Har löst om frågan men vet ej om svaret är korrekt :
1) Arean för cirkel sektorn : 60/360*10^2*3,14=52cm^2
52*2 för vi har 2 st cirkel sektorer=104cm^2
2) ( 2*10)*2=40cm^2
3) vi måste ta reda på cirkel bågens längd
då tar man 60/360*20*3,14=10,5
Arean blir 10,5*2=21cm^2
totala begränsningsarean blir 104+40+21=165cm^2
Tänker jag rätt? Är svaret korrekt ??
Bra! Nu tänker du rätt men du avrundar till närmevärden för tidigt i uträkningarna. Om du hade gjort avrundningen på slutet så hade du fått svaret 166 cm^2 istället.
Tack så mycket för hjälpen !!!
