Lastbilen ska köra igenom tunnel
Hej!
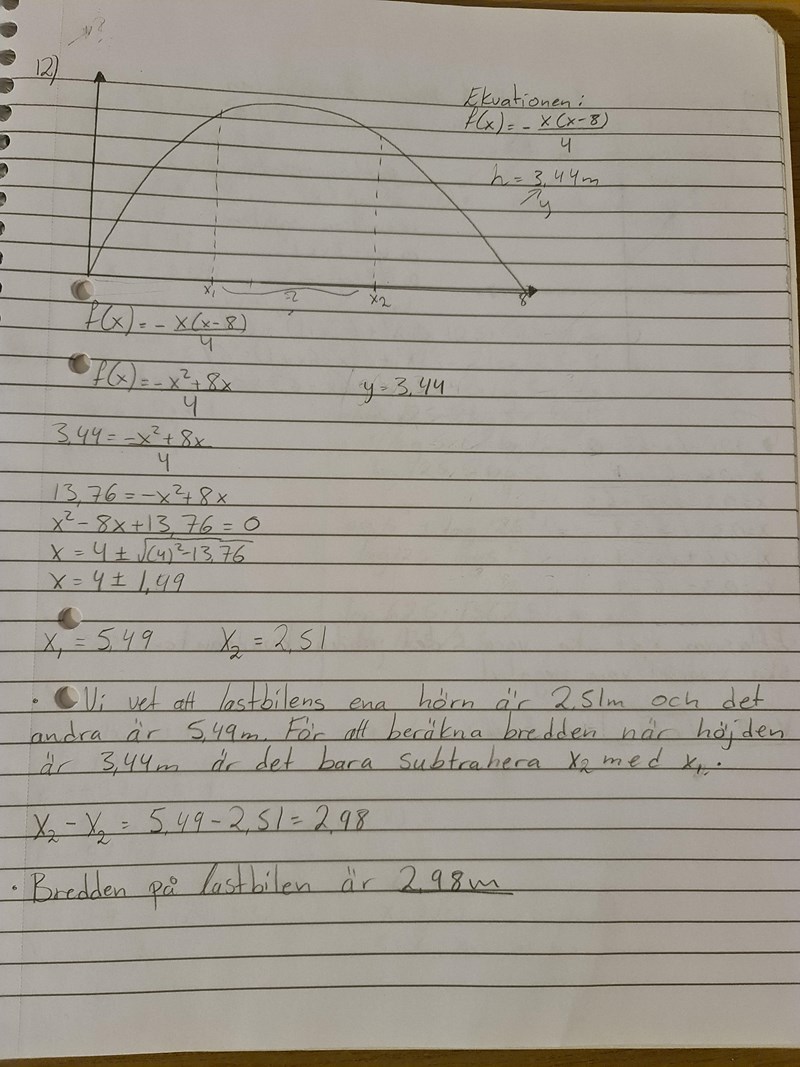
Jag har en fråga där man ska beräkna den största bredden på en lastbil när den går genom tunnel, dock så sa läraren att det är rätt men att man inte kan få full poäng för det. Jag vet inte riktigt vad som saknas för det så skulle uppskatta om någon hjälpa mig.
Ekvationen är:
Skriv en rubrik som beskriver trådens innehåll, så blir det lättare att hitta den, och bättre ordning på forumet. Ett förslag är "Lastbil ska köra igenom en tunnel". Du kan ändra din rubrik i två timmar genom att trycka på "Redigera"-knappen. /moderator
Någon?
Ser inget skäl till poängavdrag för ditt svar. Däremot är frågan märkligt ställd - som om en lastbil skulle köra in i en tunnel utan marginaler.
Hmm jag kan inte heller tänka på något annat än dessa värde för x, och de ville veta den största bredden på lastbilen när höjden är 3,44. Så när vi hade två x-värde subtraherade jag bort de för att få skillnaden...men förstår inte vart det kan vara fel..
Det är inte tillåtet att bumpa sin tråd inom tjugofyra timmar efter att tråden postats, eller inom tjugofyra timmar efter trådens senaste inlägg. Att bumpa innebär att skriva ett inlägg som inte bidrar med mer information till tråden, exempelvis "Någon??". Bumpning gör trådar svårlästa. /moderator
Somm skrev:..., dock så sa läraren att det är rätt men att man inte kan få full poäng för det.
Det finns ett par saker vad gäller formalia, som t.ex att du bör skriva istället för = och att du bör svara "Lastbilens maximala bredd är ..."..
Sedan kan vi spekulera: Tanken kanske är att tunneln är tvåfilig och att lastbilen därmed måste få plats på halva bredden.
Men bara dn lärare vet vilka krav som måste uppfyllas för att få full poäng.
Fråga helt enkelt din lärare hur du skulle ha gjort för att få full poäng.
Okej, men ser annars svaret rätt ut?
Jag ser ett avrundningsfel.
, inte
Tycker ni att man ska avrunda till 1,497 eller 1,5?
Avrunda inte alls i själva uträkningarna utan endast vid slutet.
Det bästa är att behålla rotutttycket genom hela beräkningen. Du kommer då att komma fram till att maxbredden är meter (om lastbilen kan nyttja hela tunnelbredden).
Nu ska jag också vara lite petig genom att säga att din funktion f(x) borde transformeras till en funktion g(x) istället.
Det betyder att g(x)=f(x)-3.44 och att det du ska göra är att finna rötterna till g(x)=0.
Vad tror du om det?
Jaha, ni tänker så. men jag satt g(x) som 3,44 för att visa att den är ett y-värde, kan man inte göra så?
Somm skrev:Jaha, ni tänker så. men jag satt g(x) som 3,44 för att visa att den är ett y-värde, kan man inte göra så?
Jo - alla dagar i veckan, men det är oftast så att läraren ute efter något som ni lärt er på lektionen eller enligt plan som han vill att du visar i uppgiften. Handlar inte alltid om att bara lösa uppgiften, utan att lösa det på "rätt" sätt. Vad som är "rätt" beror mycket på att du känner din lärares syfte med att ställa frågan.
Du satte f(x)=3.44 och löste ut rötterna, vilket också ger rätt svar. Men min tanke var att om ni pratat kring transformation av funktioner så är det här en perfekt uppgift för att visa just det.
Du behöver inte införa någon ny funktion.
Det går utmärkt att göra som du har gjort.
Bortsett från de tidigare kommentarerna.
Yngve skrev:Du behöver inte införa någon ny funktion.
Det går utmärkt att göra som du har gjort.
Bortsett från de tidigare kommentarerna.
Här kommer Yngve ...
Euclid skrev:
Här kommer Yngve ...
Vad menar du?
Eftersom vid frågan är är höjden 3,44 och därför satt jag den som y-värdet och för funktionen så kommer vi få ut vad x-värdet är... Jag ska se över det jag har gjort en gång till för att se om kanske värdet blev fel
Somm skrev:Eftersom vid frågan är är höjden 3,44 och därför satt jag den som y-värdet och för funktionen så kommer vi få ut vad x-värdet är... Jag ska se över det jag har gjort en gång till för att se om kanske värdet blev fel
Du har inte gjort något fel så gå till din lärare och ta reda på vad du skulle behövt redovisa för att få full pott. Kom sedan tillbaka till den här tråden och berätta.
Absolut!
Yngve skrev:Avrunda inte alls i själva uträkningarna utan endast vid slutet.
Det bästa är att behålla rotutttycket genom hela beräkningen. Du kommer då att komma fram till att maxbredden är meter (om lastbilen kan nyttja hela tunnelbredden).
Jag har en fråga, vart fick ni 2 ifrån? Den som är framför rotenur tecknet, det ska ju stå där 4 vilket är hälften av 8?
Somm skrev:
Jag har en fråga, vart fick ni 2 ifrån? Den som är framför rotenur tecknet, det ska ju stå där 4 vilket är hälften av 8?
Okej, tack för svaret!!




