Behöver hjälp med att förenkla det här uttrycket
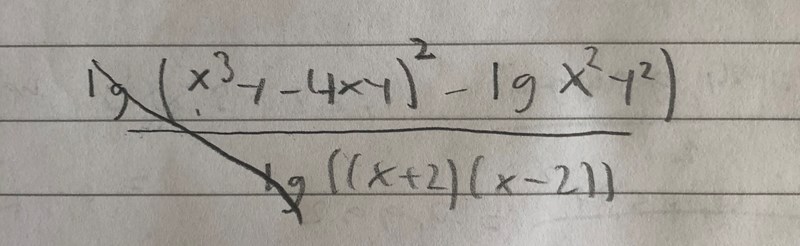
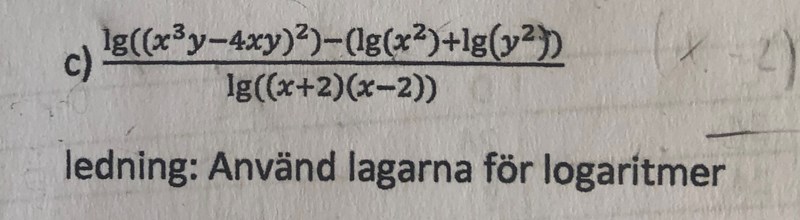
En sak som jag missade i början var att det är log på hela täljaren.
Det jag kom fram till är bilden längst upp, jag undrar även om det är ok att stryka log på det där sättet. Man kan förenkla nämnaren till x^2-4, men annars kan man väll inte förenkla det mer (den här uppgiften ska göras utan miniräknare).
Andyhoff02 skrev:
En sak som jag missade i början var att det är log på hela täljaren.
Det jag kom fram till är bilden längst upp, jag undrar även om det är ok att stryka log på det där sättet. Man kan förenkla nämnaren till x^2-4, men annars kan man väll inte förenkla det mer (den här uppgiften ska göras utan miniräknare).
Hej och välkommen till Pluggakuten!
Nej det är inte "log på hela täljaren"
Titta noga och räkna parenteser.
Se om du kan faktorisera något.
Har du prövat att använda tipset du fick i uppgiften?
Enligt en logaritm lag lg A - lg B= lg A/B
så kan jag ju skriva om det till:
lg ((x^3-4xy)^2/x^2y^2/ lg x^2-4
är jag på rätt väg?
Därifrån kan man väll stryka log, och sedan bryta ut xy så att det blir xy(x^2-4)^2/xy(xy)/x^2-4
därefter kan man stryka xy så att man får (x^2-4)^2/xy/x^2-4
sedan multiplicerar man x^2-4)^2/xy med 1/x^2-4 så att man kan stryka en x^2-4 ”snett”, då får man x^2-4/xy <=> x-4/y
har jag rätt?
Det är svårt att tolka vad du skriver om du inte använder fler parenteser.
Om du menar så måste du skriva parenteser runt hela täljaren och hela nämnaren, så här (a-b)/(c-d).
----------------
Ett annat alternativ är att använda formeleditorn.
Du hittar den bland ikonerna ovanför den text du skriver, den ser ut som ett "rotenur"-tecken.
----------------'
Men nej, du kan inte "stryka log", för då ändrar du uttryckets värde.
Tror jag lyckades lösa den! Man kan nog göra det på ett lättare sätt dock.

EDIT - ser nu att du löste den
Tips:
- Faktorisera .
- Använd logaritmlag för att dela upp täljarens första term i flera termer.
- Förenkla täljaren.
Visa dina försök.
Hur fortsätter jag?

Jag tror jag lyckades lösa den, men finns antagligen flera lösningar som är mer effektiva, jag försökte påbörja en lösning m.h.a dina tips, men gick inte så bra.
Jag tänkte så här:
Täljaren:
Faktorisera:
Logaritmlag sista termerna:
Logaritmlag första termen:
Förenkla:
Logaritmlag:
Nämnaren:
Konjugatregel:
Yngve skrev:Jag tänkte så här:
lg((xy)2(x2−4)2)−(lg(x2)+lg(y2)
Varför kan man faktorisera ut (xy)^2? Jag får xy som största möjliga faktor att bryta ut


