Beräkna A^n

$\hat{A}$ är nääästan diagonal men det innebär att den kan delas upp i en diagonal del och och en ickediagonal del

$\hat{A} = D + N$

där man kan utveckla $(A + D)^n$ och inse att det är något speciellt som sker med $N$-potenserna. 

Vi har diskuterat tricket i några tidigare trådar, exempelvis i https://www.pluggakuten.se/trad/berakna-matrisen-a-med-exponenten-19/ 

SeriousCephalopod skrev:

$\hat{A}$ är nääästan diagonal men det innebär att den kan delas upp i en diagonal del och och en ickediagonal del

$\hat{A} = D + N$

där man kan utveckla $(A + D)^n$ och inse att det är något speciellt som sker med $N$-potenserna. 

Vi har diskuterat tricket i några tidigare trådar, exempelvis i https://www.pluggakuten.se/trad/berakna-matrisen-a-med-exponenten-19/ 

Såhär har jag börjat men fastnat nu, hur kan jag fortsätta, om jag nu är på rätt spår?

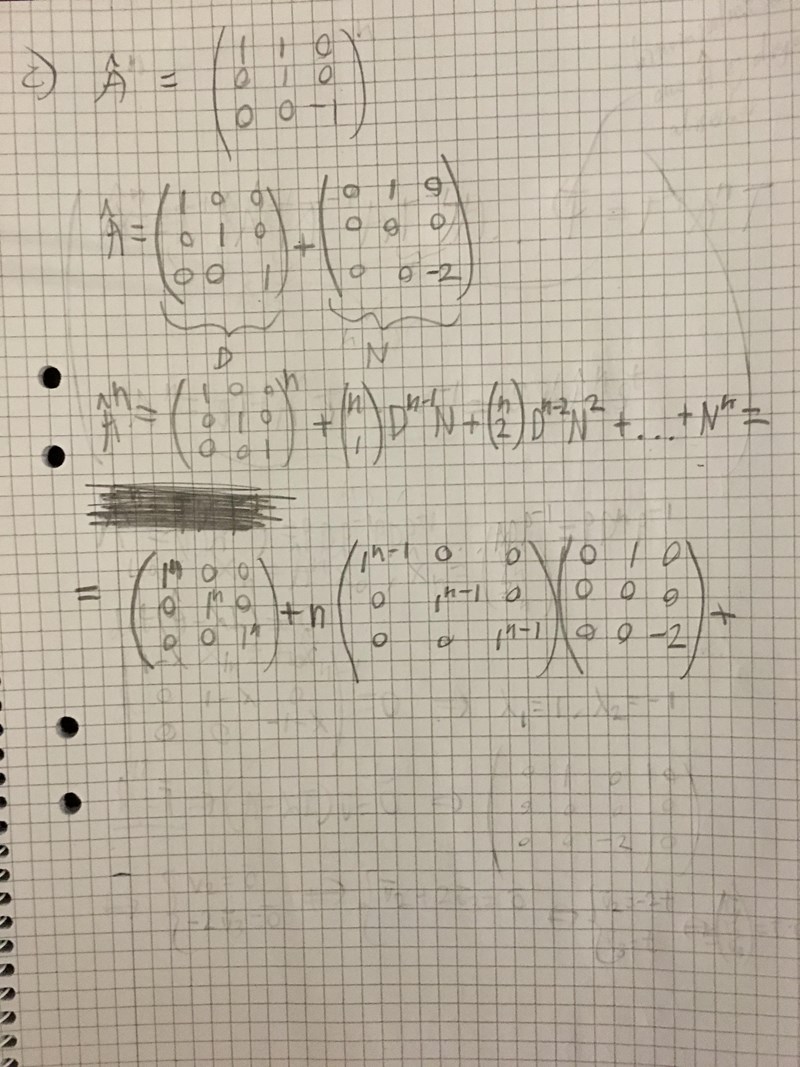
(skippar hatt på A-matrisen)

Det du gör är en annan metod än den jag föreslog även om språket var tvetydligt. Idén från den andra tråden är att lägga de diagonala elementen i D och att de övriga som inte är på diagonalen ligger i N.

$A = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1\end{pmatrix} + \begin{pmatrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}$

Poängen är att 

$\begin{pmatrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}^2 = 0$

så dess högre potenser försvinner. 

Man kan förstås köra på din metod också men då skulle jag skriva

$A = I + B$

för att betona att den vänstra är enhetsmatrisen men inte nödvändigtvis är samma som de diagonala elementen i A och blir inte riktigt lika rakt. 

SeriousCephalopod skrev:

(skippar hatt på A-matrisen)

Det du gör är en annan metod än den jag föreslog även om språket var tvetydligt. Idén från den andra tråden är att lägga de diagonala elementen i D och att de övriga som inte är på diagonalen ligger i N.

$A = \begin{pmatrix}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & -1\end{pmatrix} + \begin{pmatrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}$

Poängen är att 

$\begin{pmatrix}0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0\end{pmatrix}^2 = 0$

så dess högre potenser försvinner. 

Man kan förstås köra på din metod också men då skulle jag skriva

$A = I + B$

för att betona att den vänstra är enhetsmatrisen men inte nödvändigtvis är samma som de diagonala elementen i A och blir inte riktigt lika rakt. 

Tack så mycket igen! Vad enkelt det blev nu!