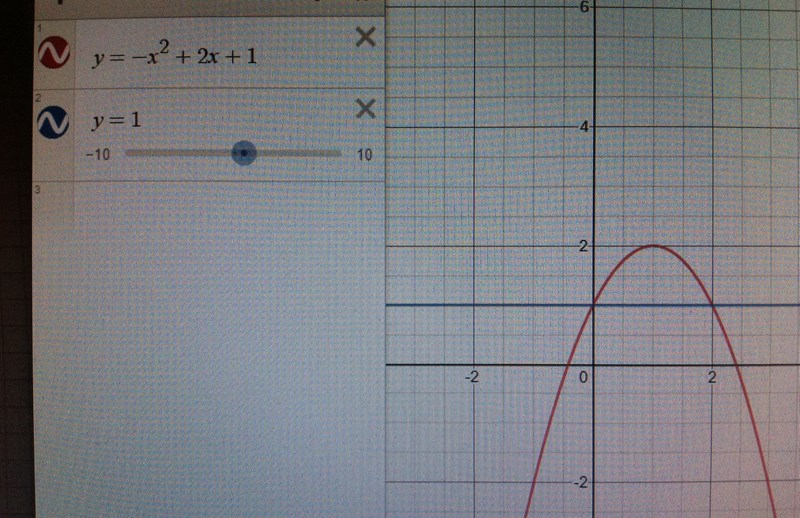
Beräkna arean av det område som begränsas av funktioner y1=-x^2 + 2x + 1 och y2= 1.

Det är en bra början! Nu behöver du integrera din integrand (integrand är det som står mellan $\int$ och "dx"). Har du integrerat polynom tidigare? Om inte, eller om du behöver fräscha upp dina kunskaper, kan du läsa om integration här. :)

Ser ut som en bra början. Nu måste du integrera innan du kan stoppa in gränserna.

Yes! Har gjort det tidigare men förstår inte hur jag ska göra integraler och räkna ut när de är -x^2? 

Niki skrev:

Yes! Har gjort det tidigare men förstår inte hur jag ska göra integraler och räkna ut när de är -x^2? 

Tänk att det istället stog -(x^2). dvs du kan bara integrera x^2, det blir exakt samma sak bara att du har ett minus med.

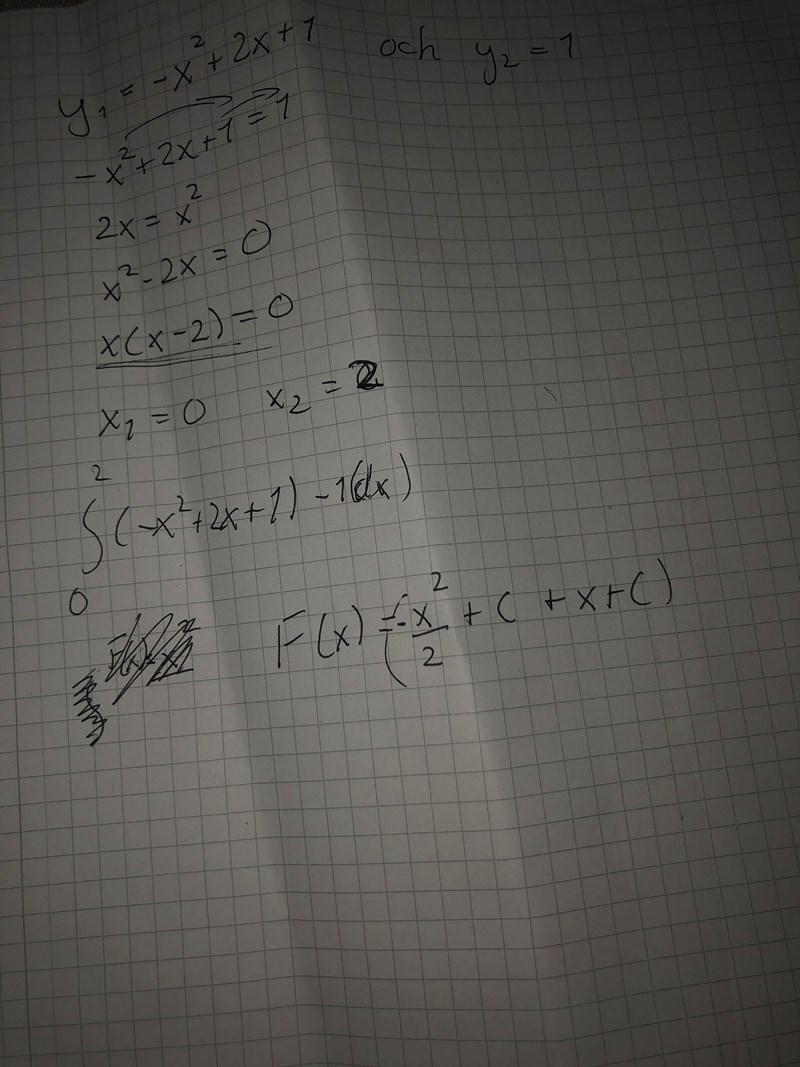ser detta lite bättre ut? Alltså gör jag F(x)? 

Vad är det som blir  $-x^{2 }$

     Jo det är   $-\frac{x^3}{3}$

Glöm inte att formeln för derivering är $n{a}^{n-1}$ och integrering ska vara tvärtom det vill säga: $\frac{a^{n+1}}{n+1}$
du har integrerat $-x^2$till $-\frac{x^2}{2} dvs du har gjort:\hspace{0.17em}\frac{a^n}{n}$
Sedan vet jag inte vart du trollar bort 2x någonstans eftersom  $\int$ $2x\ne 0$och bör därför vara inkluderad.

En annan sak, du ska inte lägga till +C efter varje term du integrerar. antag att du har $f\left(x\right)=a{x}^3+b{x}^2+cx+d$
integrerar du detta får du: $F\left(x\right)=\frac{a{x}^4}{4}+\frac{b{x}^3}{3}+\frac{c{x}^2}{2}+dx+C$
Du lägger till C eftersom $\int x^2 =\frac{x^3}{3}+C$ oavsett vad C är så kommer derivatan av $\frac{x^3}{3}$alltid att vara $x^2$ och eftersom derivatan av en konstant C = 0 så spelar det inte roll vad C är och därför finns det oändligt många funktioner som är en primitiv funktion till $x^2$ och av denna anledning lägger vi  till +C efter vi integrerat en funktion för att täcka alla konstanter där $C\in \mathrm{ℝ}$