Beräkna arean av markerat område under graf
Hej!
Sitter med en uppgift som handlar om integraler.
Uppgiften ser ut såhär:
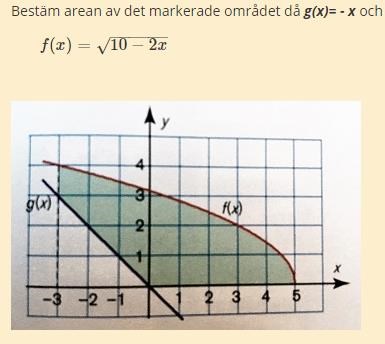
Hittills har jag försökt beräkna de primitiva funktionerna av f(x) och g(x). Har kommit fram till följande:
F(x) = (10-2x)1/2
G(x) = (2/3)*x(1+1/2) + C
Här fastnar jag dock och kommer inte vidare.
Det finns en generell formel för uträkning av integraler, men jag förstår inte riktigt hur jag ska stoppa in mina värden i den.
Som jag förstått det så räknas det ut genom f(x)dx = F(b)-F(a).
Uppskattar all hjälp!
Dina primitiva funktioner är inte korrekta. Visa hur du har fått fram dem, så kan vi hjälpa dig att hitta var det har blivit fel.
Om du deriverar det G(x) du räknat ut nu, vad får du då? Kika i det här formelbladet:
https://www.formelsamlingen.se/media/2019301/formelblad_matematik_4.pdf
och titta vid primitiva funktioner. -x är ju samma sak som eller hur?
Din F(x) stämmer inte heller eftersom att sqrt(10-2x) är samma sak som (10-2x)^(1/2). Här måste du använda en räkneregel för att hitta den primitiva funktionen, vet du vilken?
Tar du integralen av f(x) får du hela arean under grafen ner till x-axeln. Samma sak för g(x)
Smaragdalena skrev:Dina primitiva funktioner är inte korrekta. Visa hur du har fått fram dem, så kan vi hjälpa dig att hitta var det har blivit fel.
g(x) = x^½ => G(x) = (2/3)*x^(1+½) + konstant.
Det första jag tänkte dock var att G(x) = (-x2)/2.
f(x) tog jag hjälp av en calculator på nätet, visste inte riktigt hur man får fram en primitiv funktion av roten ur 10-2x.
Tomte123 skrev:Om du deriverar det G(x) du räknat ut nu, vad får du då? Kika i det här formelbladet:
https://www.formelsamlingen.se/media/2019301/formelblad_matematik_4.pdf
och titta vid primitiva funktioner. -x är ju samma sak som eller hur?
Din F(x) stämmer inte heller eftersom att sqrt(10-2x) är samma sak som (10-2x)^(1/2). Här måste du använda en räkneregel för att hitta den primitiva funktionen, vet du vilken?
Tar du integralen av f(x) får du hela arean under grafen ner till x-axeln. Samma sak för g(x)
Är det kedjeregeln jag behöver använda för sqrt(10-2x)?
filipsrbin skrev:
Är det kedjeregeln jag behöver använda för sqrt(10-2x)?
Ja, kedjeregeln "baklänges".
Men du behöver inte krångla med det här.
Det är mycket enklare och snabbare att pröva sig fram genom att
- gissa en primitiv funktion.
- Derivera och jämföra.
- Gissa en ny bättre primitiv funktion.
- Derivera och jämföra.
O.s.v. tills du hamnar rätt.
-----------
Typ så här:
Du söker en primitiv funktion till .
Den bör vara något som liknar .
Vi prövar att derivera och får då, med hjälp av kedjeregeln, .
Det är ju nästan rätt, det är bara en faktor 3 som skiljer. Då gissar vi på en annan primitiv funktion, där vi har kompenserat för denna faktor ...
Kan du fortsätta själv?
Yngve skrev:filipsrbin skrev:Är det kedjeregeln jag behöver använda för sqrt(10-2x)?
Ja, kedjeregeln "baklänges".
Men du behöver inte krångla med det här.
Det är mycket enklare och snabbare att pröva sig fram genom att
- gissa en primitiv funktion.
- Derivera och jämföra.
- Gissa en ny bättre primitiv funktion.
- Derivera och jämföra.
O.s.v. tills du hamnar rätt.
-----------
Typ så här:
Du söker en primitiv funktion till .
Den bör vara något som liknar .
Vi prövar att derivera och får då, med hjälp av kedjeregeln, .
Det är ju nästan rätt, det är bara en faktor 3 som skiljer. Då gissar vi på en annan primitiv funktion, där vi har kompenserat för denna faktor ...
Kan du fortsätta själv?
Suttit i snart 1h men kommer inte fram till något. Det som gör det svårt för mig, det är just sqrt 10, får inte fram vad det skulle kunna vara.
Yngve skrev:filipsrbin skrev:Är det kedjeregeln jag behöver använda för sqrt(10-2x)?
Ja, kedjeregeln "baklänges".
Men du behöver inte krångla med det här.
Det är mycket enklare och snabbare att pröva sig fram genom att
- gissa en primitiv funktion.
- Derivera och jämföra.
- Gissa en ny bättre primitiv funktion.
- Derivera och jämföra.
O.s.v. tills du hamnar rätt.
-----------
Typ så här:
Du söker en primitiv funktion till .
Den bör vara något som liknar .
Vi prövar att derivera och får då, med hjälp av kedjeregeln, .
Det är ju nästan rätt, det är bara en faktor 3 som skiljer. Då gissar vi på en annan primitiv funktion, där vi har kompenserat för denna faktor ...
Kan du fortsätta själv?
Kikade på en video nu och om jag förstår det rätt så, när man har sqrt av ett tal och ska göra om det till en primitiv funktion, så kan man skriva om det till x1/2, eller hur?
Exempelvis :
f(x) = sqrt(x) + 4
Detta kan man skriva om som x1/2 + 4
Och primitiva funktionen blir då F(x) = x1,5 / 1,5 + 4x + C
Så om vi tar mitt exempel, f(x) = sqrt(10x-2)
Kan man då skriva om detta som (10x-2)1/2?
Då blir F(x) = ((10x-2)1,5)/1,5
Är jag på rätt bana?
filipsrbin skrev:
Kikade på en video nu och om jag förstår det rätt så, när man har sqrt av ett tal och ska göra om det till en primitiv funktion, så kan man skriva om det till x1/2, eller hur?Exempelvis :
f(x) = sqrt(x) + 4Detta kan man skriva om som x1/2 + 4
Och primitiva funktionen blir då F(x) = x1,5 / 1,5 + 4x + C
Ja det stämmer. Och det kan du kolla själv genom att derivera ditt förslag på primitiv funktion F(x). Derivatan ska då vara lika med originalfunktionen f(x).
Så om vi tar mitt exempel, f(x) = sqrt(10x-2)
Kan man då skriva om detta som (10x-2)1/2?
Ja det stämmer, förutom att det var 10-2x, inte 10x-2.
Då blir F(x) = ((10x-2)1,5)/1,5
Är jag på rätt bana?
Pröva!
Derivera F(x). Blir derivatan lika med f(x)?
I så fall är F(x) en primitiv funktion till f(x), annars inte.
Yngve skrev:filipsrbin skrev:Kikade på en video nu och om jag förstår det rätt så, när man har sqrt av ett tal och ska göra om det till en primitiv funktion, så kan man skriva om det till x1/2, eller hur?Exempelvis :
f(x) = sqrt(x) + 4Detta kan man skriva om som x1/2 + 4
Och primitiva funktionen blir då F(x) = x1,5 / 1,5 + 4x + C
Ja det stämmer. Och det kan du kolla själv genom att derivera ditt förslag på primitiv funktion F(x). Derivatan ska då vara lika med originalfunktionen f(x).
Så om vi tar mitt exempel, f(x) = sqrt(10x-2)
Kan man då skriva om detta som (10x-2)1/2?
Ja det stämmer, förutom att det var 10-2x, inte 10x-2.
Då blir F(x) = ((10x-2)1,5)/1,5
Är jag på rätt bana?
Pröva!
Derivera F(x). Blir derivatan lika med f(x)?
I så fall är F(x) en primitiv funktion till f(x), annars inte.
Verkar inte ha blivit rätt :(.. Vet inte hur jag ska räkna ut detta ..
filipsrbin skrev:
Verkar inte ha blivit rätt :(.. Vet inte hur jag ska räkna ut detta ..
Du har att
Börja därför med att gissa att
Visa nu hur du gör när du deriverar så fortsätter vi därifrån.
Yngve skrev:filipsrbin skrev:Verkar inte ha blivit rätt :(.. Vet inte hur jag ska räkna ut detta ..Du har att
Börja därför med att gissa att
Visa nu hur du gör när du deriverar så fortsätter vi därifrån.
Kan detta stämma?
F'(x)=1.5(10-2x)^0.5*(-2)=-3(10-2x)^0.5
filipsrbin skrev:
Kan detta stämma?F'(x)=1.5(10-2x)^0.5*(-2)=-3(10-2x)^0.5
Ja det stämmer.
Och det är ju nästan rätt, eller hur?
Det är bara en faktor som skiljer detta från f(x).
- Vilken faktor?
- Hur ska du modifiera F(x) så att denna faktor "försvinner" när du deriverar?
Yngve skrev:filipsrbin skrev:Kan detta stämma?F'(x)=1.5(10-2x)^0.5*(-2)=-3(10-2x)^0.5
Ja det stämmer.
Och det är ju nästan rätt, eller hur?
Det är bara en faktor som skiljer detta från f(x).
- Vilken faktor?
- Hur ska du modifiera F(x) så att denna faktor "försvinner" när du deriverar?
1. Faktor "3". Den finns inte med i f(x).
2. Kommer inte fram till något, kanske man kan göra om potensen på något sätt? Känns som att den måste bli 1 för att det ska gå ihop..
filipsrbin skrev:
1. Faktor "3". Den finns inte med i f(x).
Ja det stämmer.
2. Kommer inte fram till något, kanske man kan göra om potensen på något sätt? Känns som att den måste bli 1 för att det ska gå ihop..
Tänk på att derivatan av . Pröva alltså att multiplicera ditt förslag på primitiv funktion med konstanten , dvs sätt .
Derivera nu . Vad får du då?
Yngve skrev:filipsrbin skrev:1. Faktor "3". Den finns inte med i f(x).
Ja det stämmer.
2. Kommer inte fram till något, kanske man kan göra om potensen på något sätt? Känns som att den måste bli 1 för att det ska gå ihop..
Tänk på att derivatan av . Pröva alltså att multiplicera ditt förslag på primitiv funktion med konstanten , dvs sätt .
Derivera nu . Vad får du då?
Asså förlåt Yngve men jag har helt hjärnsläpp. Förstår verkligen inte hur jag ska göra, känner mig som ett hopplöst mattefall haha.. ;-;
filipsrbin skrev:
Asså förlåt Yngve men jag har helt hjärnsläpp. Förstår verkligen inte hur jag ska göra, känner mig som ett hopplöst mattefall haha.. ;-;
Om så är .
Du vill att detta ska vara lika med .
Det blir det om du väljer så att , dvs om du väljer .
Sätt alltså .
Derivera nu och försäkra dig om att derivatan är lika med
Yngve skrev:filipsrbin skrev:Asså förlåt Yngve men jag har helt hjärnsläpp. Förstår verkligen inte hur jag ska göra, känner mig som ett hopplöst mattefall haha.. ;-;Om så är .
Du vill att detta ska vara lika med .
Det blir det om du väljer så att , dvs om du väljer .
Sätt alltså .
Derivera nu och försäkra dig om att derivatan är lika med
Ja men nu blev det ju rätt! :-D
Så min primitiva funktion för f(x) är alltså F(x) = −1/3*(10-2x)1,5.
Sen har vi g(x) som då = -x
Om jag försöker själv nu så får jag fram att G(x) = -x2/2 + C.
Stämmer det?
Primiriv funktion av g(x):
G(x)= (-x2 /2)
Primitiv funktion av f(x):
Funktionen: (10-2x)1/2
a(bx+c)d dx =[ ] <= följ formeln:
(10-2x)1/2 = ((10-2x)((1/2)+(2/2)) )/-2*(3/2) = =
F(x)= -1/3 * (10-2x)3/2
behöver du hjälp med Arean?
tajmahal skrev:Primiriv funktion av g(x):
G(x)= (-x2 /2)
Primitiv funktion av f(x):Funktionen: (10-2x)1/2
a(bx+c)d dx =[ ] <= följ formeln:
(10-2x)1/2 = ((10-2x)((1/2)+(2/2)) )/-2*(3/2) = =
F(x)= -1/3 * (10-2x)3/2behöver du hjälp med Arean?
Tack! Ja, eller iallafall vägleda mig hur jag ska komma fram till arean! Vad jag vet om så ska jag använda mig av integraler för att räkna ut den, eller hur?
Ja precis, du ska ta den övre funktionen minus den undre funktionen. från -3 till 0 tar du(F(0)-F(-3))-(G(0)-G(-3))
sen från 0 till 5 tar du bara F(5)-(F0)
summerar sedan areorna
tajmahal skrev:Ja precis, du ska ta den övre funktionen minus den undre funktionen. från -3 till 0 tar du(F(0)-F(-3))-(G(0)-G(-3))
sen från 0 till 5 tar du bara F(5)-(F0)
summerar sedan areorna
Okej då försöker jag mig på det imorgon, är så trött nu hehe.. Tusen tack för hjälpen! Om jag fastnar postar jag i denna tråd igen:-)!
Här kan du läsa om integraler och areor: https://www.matteboken.se/lektioner/matte-3/integraler/berakning-av-integraler.
tajmahal skrev:Ja precis, du ska ta den övre funktionen minus den undre funktionen. från -3 till 0 tar du(F(0)-F(-3))-(G(0)-G(-3))
sen från 0 till 5 tar du bara F(5)-(F0)
summerar sedan areorna
Med det du skrev där så blir det alltså :
-1/3*(10-2*0)3/2 + 1/3*(10-2*(-3))3/2 + 02 /2 + (-3)2 /2 ?
Stämmer det? Eller har jag ställt upp det fel?




