beräkna arena av begränsat område (envariabelanalys)

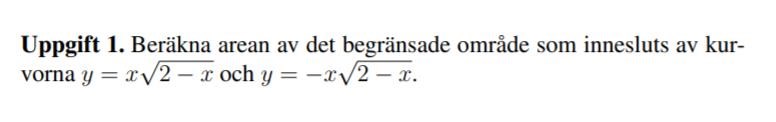
Jag tänker att jag ska beräkna en integral för att få fram arean. då behöver jag två integralgränser och tänker att de får jag fram där de korsar varandra eller har som gemensampunkt?

när jag har det så ska jag beräkna själva integralen men hur får jag fram den? eller ska jag räkna först en integralen för ena y och sen andra integralen för det andra y och sen addera dessa?

eller ska man tillämpa något annat verktyg?

Du tänker helt rätt med att hitta skärningspunkterna mellan kurvorna för att få integralgränserna! Vad det gäller integranden, arean mellan funktionerna f(x) och g(x) kan beräknas som $\int_{a}^{b} (f (x) - g (x)) d x$ , där $f (x) \geq g (x), x \in [a, b]$ . :)

Precis. Gränser fås genom att sätta y-värdena lika med varandra.

Du måste reda ut vilken av dessa två som är "övre funktion" resp. "undre funktion" för att få rätt tecken i slutliga svaret.

jaha okej okej kanske inte var krångligare än så, men då antar jag att den övre är den som inte har negativ, jag ska testa

Jo, det stämmer, men jobba in vanan att alltid kontrollera vilken funktion som ligger överst. Sätt in exempelvis x = 1 och se vilken kurva som är överst. :)

Smutstvätt skrev:
Jo, det stämmer, men jobba in vanan att alltid kontrollera vilken funktion som ligger överst. Sätt in exempelvis x = 1 och se vilken kurva som är överst. :)

jaha okej tack tänkte inte på det. då sätter jag in ett värde och ser vilket funktionsvärde är störst och den blir då den övre? kan det inte då inte finnas vissas punkter där den undre har större värde än den övre? eller räknas det inte som undre då utan måste det gälla alla punkter?

EDIT: har fått till svar 4/3 som area mellan graferna, hur kan jag kontrollera att det stämmer eller inte? finns det någon metod för det?

EDIT: kom på att 4/3 var fel men undrar ändå hur man kan kontrollera det

annars så har jag i så fall $\int_{0}^{2} x \sqrt{2 - x} - (- x \sqrt{2 - x}) d x = \int_{0}^{2} 2 x \sqrt{2 - x} d x$

det ser ju inte ut som en trevlig integral att räkna ut, vad använder man för knep? har testat partiell integration men utan resultat. variabelsubstitution går säkert med någon hemlig variabel som jag inte känner ?

EDIT: okej jag tror jag löste den, eller jag fått ett svar men hur kan kan kontrollera om det är rätt eller går det ej? finns det i så fall verktyg på nätet eller annat som kan bekräfta mitt svar?

Det är alltid en bra idé att rita upp sina integraler, så att man vet vad det är man håller på med.

WolframAlpha är ofta bra för att kolla att man har fått fram rätt värde. Men det är inte alltid enkelt att komma på hur man skall skriva in sin fråga för att det skall bli rätt - inte för mig åtminstone.

Nu blev jag lite nyfiken och plottade graferna, vilka då både är över och under x-axeln. Måste man ta hänsyn till detta i sin areaberäkning, eftersom det blir symmetri kring axeln? Eller gäller det bara när det är kring y-axeln?

Du kan beräkna arean som integralen av (överkurvan -underkurvan) eller 2*(integralen av överkurvan -0), det blir samma svar. Integrationsgränserna blir samma i båda fallen.

hur löste du integralen? Har försökt jättelänge men kommer ingen vart

blairdolf skrev:
hur löste du integralen? Har försökt jättelänge men kommer ingen vart

Gör en ny tråd för din fråga, där du visar hur du har försökt och hur långt du har kommit. /moderator

Svara

Visa senaste svar