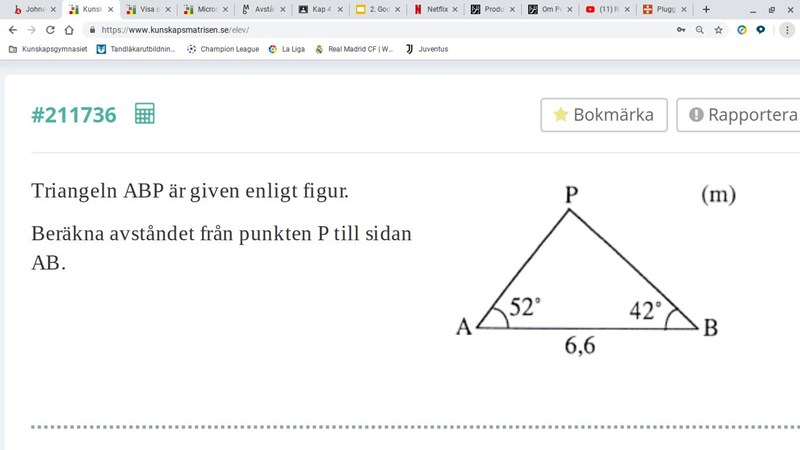
Beräkna avståndet från punkten P till sidan AB.

Vad tänker du dig att ett avstånd mellan en punkt och en linje är?

SeriousCephalopod skrev:

Vad tänker du dig att ett avstånd mellan en punkt och en linje är?

Jag vet faktiskt inte .. 

Om jag stod i ett rum och frågade om avståndet mellan mig och en specifik vägg hade du förstått vad jag menat då?

Hej!

• Dra en linje PH från punkten P ända ner till sidan AB så att linjen PH är vinkelrät mot sidan AB; avståndet från P till AB är samma sak som längden hos linjen PH.
• Linjen PH når linjen AB i punkten H. Punkten H delar in linjen AB i två delar: linjen AH och linjen HB. Låt linjen AH ha längden $x$ meter; då har linjen HB längden $(6.6-x)$ meter.
• Tangensvärdet för vinkeln 52 grader är lika med kvoten $|PH|/x$ och tangensvärdet för vinkeln 42 grader är lika med kvoten $|PH|/(6.6-x).$ Det ger dig en ekvation som bestämmer längden $x$ nämligen $x \tan 52 = PH = (6.6-x)\tan 42$ och när du känner $x$ kan du beräkna det sökta avståndet $|PH|$.

Avståndet från punkten $P$ till sidan $AB$ är triangelns höjd: $h$.

Givet att du bestämt sidan $b$ kan du uttrycka triangelns area på två sätt:

$A=\frac{6,6\cdot h}{2}=\frac{b\cdot 6,6\cdot \sin 52^{\circ}}{2}$

Utifrån detta kan du lösa ut $h$.

Metaforen jag ville till var att man tänker sig triangeln som ett rum och att man står i ett hörn och frågar vad avståndet är mellan hörnet och den motstående väggen. Från det kanske man förstår hur man kan tolka avståndsproblem i allmänhet genom att relatera till vardagsbegrepp. Problemet här var ju såvitt jag ser det att förstå frågan. Inte nödvändigtvis metod.

tomast80 skrev:

Avståndet från punkten $P$ till sidan $AB$ är triangelns höjd: $h$.

Givet att du bestämt sidan $b$ kan du uttrycka triangelns area på två sätt:

$A=\frac{6,6\cdot h}{2}=\frac{b\cdot 6,6\cdot \sin 52^{\circ}}{2}$

Utifrån detta kan du lösa ut $h$.

Tack för hjälpen! :)