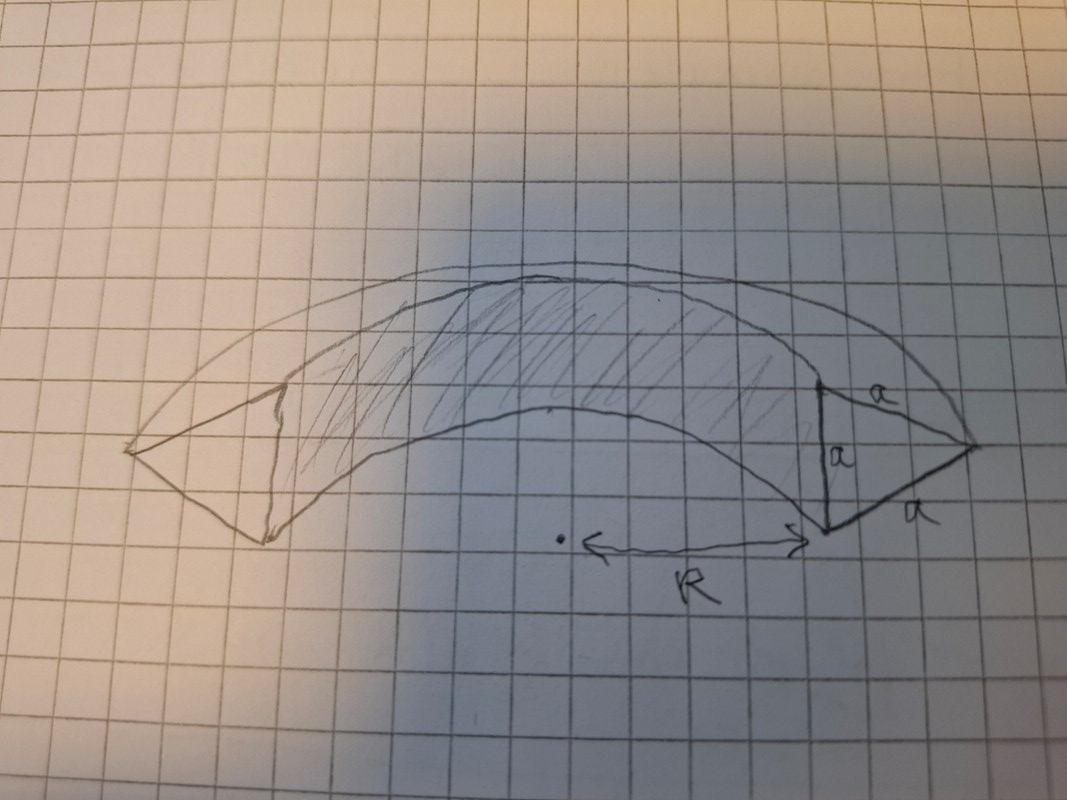
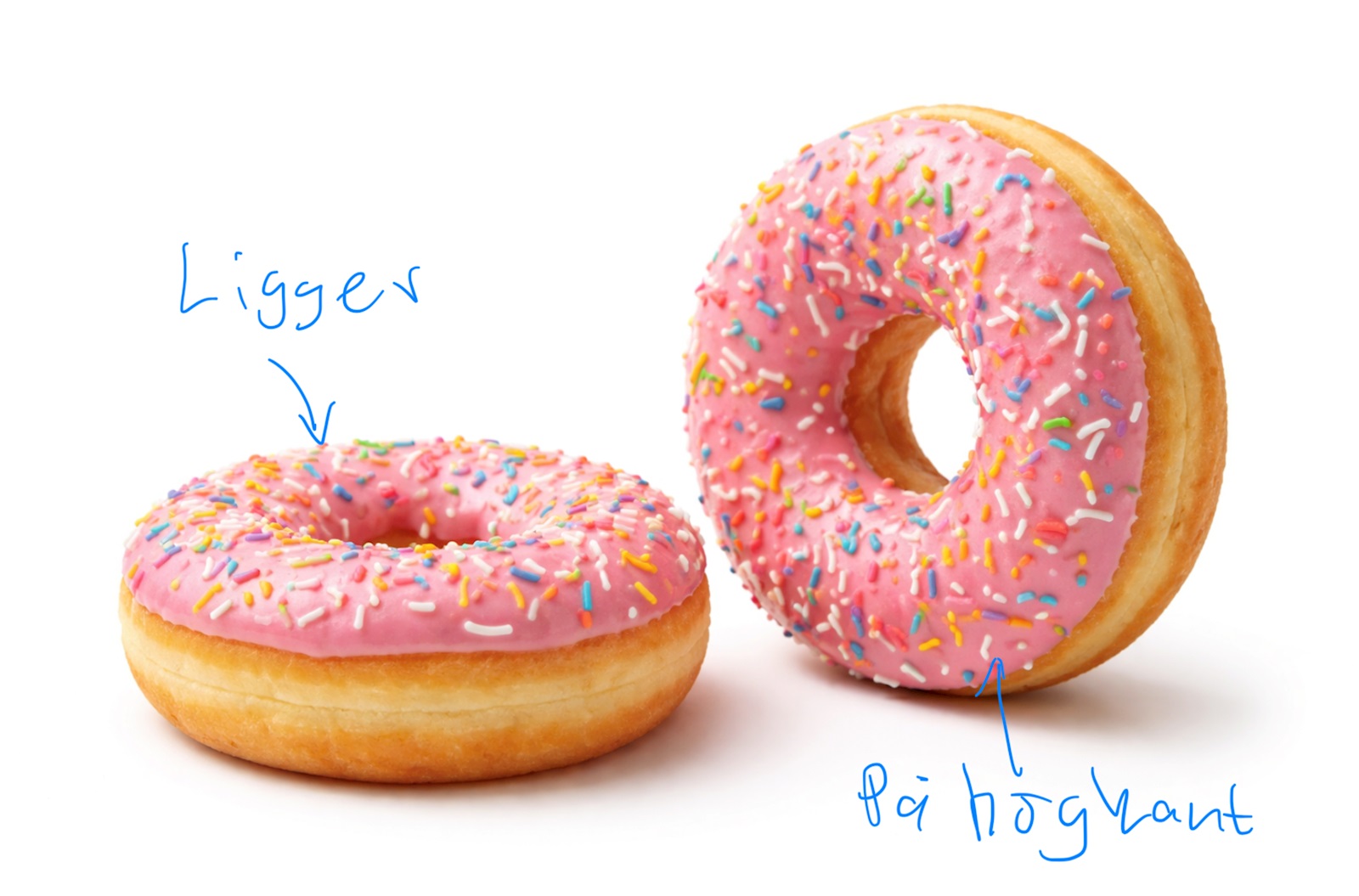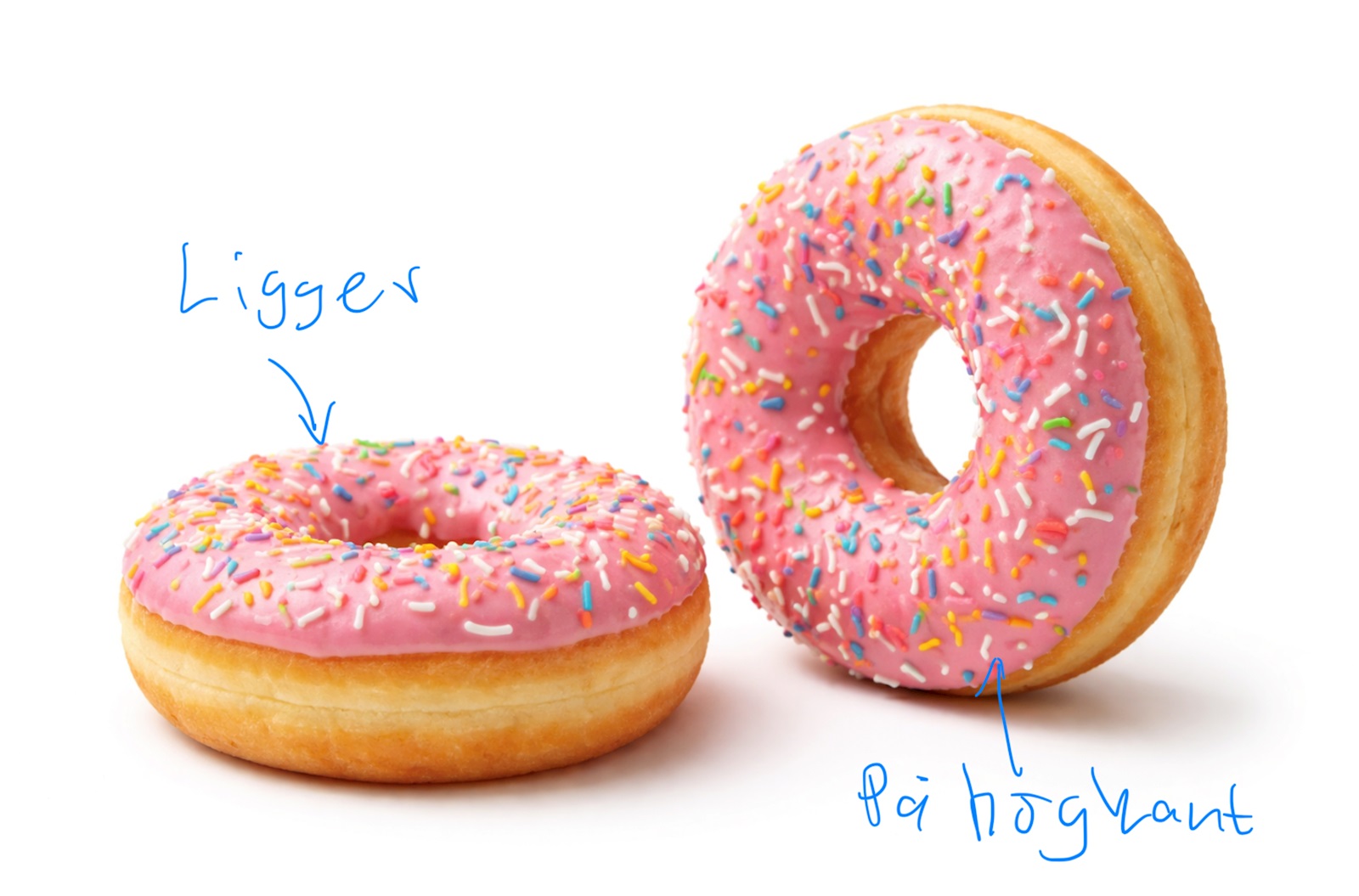Beräkna begränsningsarean och volymen V av en toroid

Hej!
Hur ska man börja här?
Använd detta.
PATENTERAMERA skrev:Använd detta.
Pappusregeln II för Volym? Hur ska jag använda den?
Du behöver veta triangelns area och var tyngdpunkten ligger i triangeln.
PATENTERAMERA skrev:Du behöver veta triangelns area och var tyngdpunkten ligger i triangeln.
Jag ser ingen triangel i figuren?
Toroidens tvärsnitt är en liksidig triangel.
PATENTERAMERA skrev:Toroidens tvärsnitt är en liksidig triangel.
Men var i figuren kan man se detta dvs Toroidens tvärsnitt är en liksidig triangel?
Det står i problemtexten.
PATENTERAMERA skrev:Det står i problemtexten.
Ja jag vet, men jag syftar på bildmässigt dvs "Toroidens tvärsnitt är en liksidig triangel"
Du får toroiden genom att rotera en liksidig triangel kring en axel.
PATENTERAMERA skrev:Du får toroiden genom att rotera en liksidig triangel kring en axel.
Hur då?
Du har ju en figur att titta på.
PATENTERAMERA skrev:Du har ju en figur att titta på.
Ja men om den figur roterar kring sin axel så ser jag inte hur det bildas en liksidig triangel? Jag vet inte om man ska rita en liksidig triangel i mitten av toroiden och sen tänka så?
Du får tänka dig hur toroiden i figuren bildas då du roterar en triangel kring toroidens cenrumaxel.
PATENTERAMERA skrev:Du får tänka dig hur toroiden i figuren bildas då du roterar en triangel kring toroidens cenrumaxel.
Vad är centrumaxel här?
Tvärtom, figuren bildas genom att rotera triangeln.
PATENTERAMERA skrev:Tvärtom, figuren bildas genom att rotera triangeln.
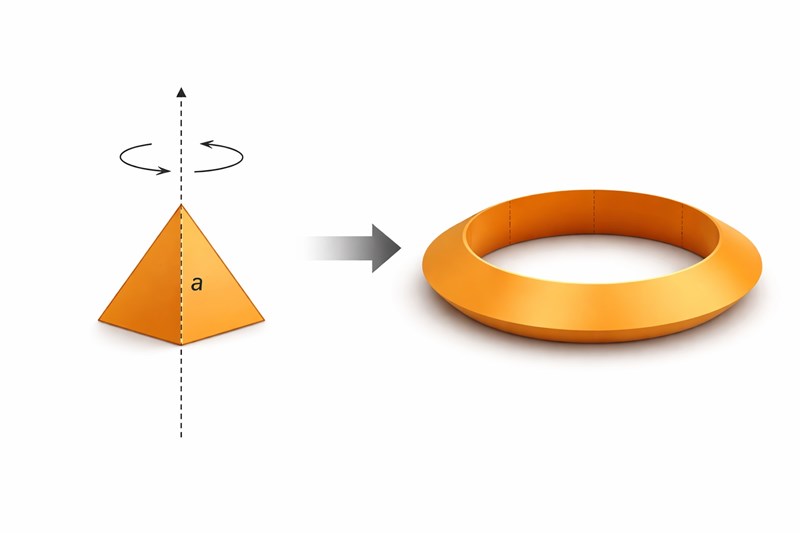
Du menar såhär? Det var svårt att tänka sig i huvudet så fick hjälp av chat.
Ok så vi känner till tyngdpunkten för en homogen triangel dvs h/3 (tror jag). Sen behöver vi triangels area för att använda oss av pappus första regeln eller hur?
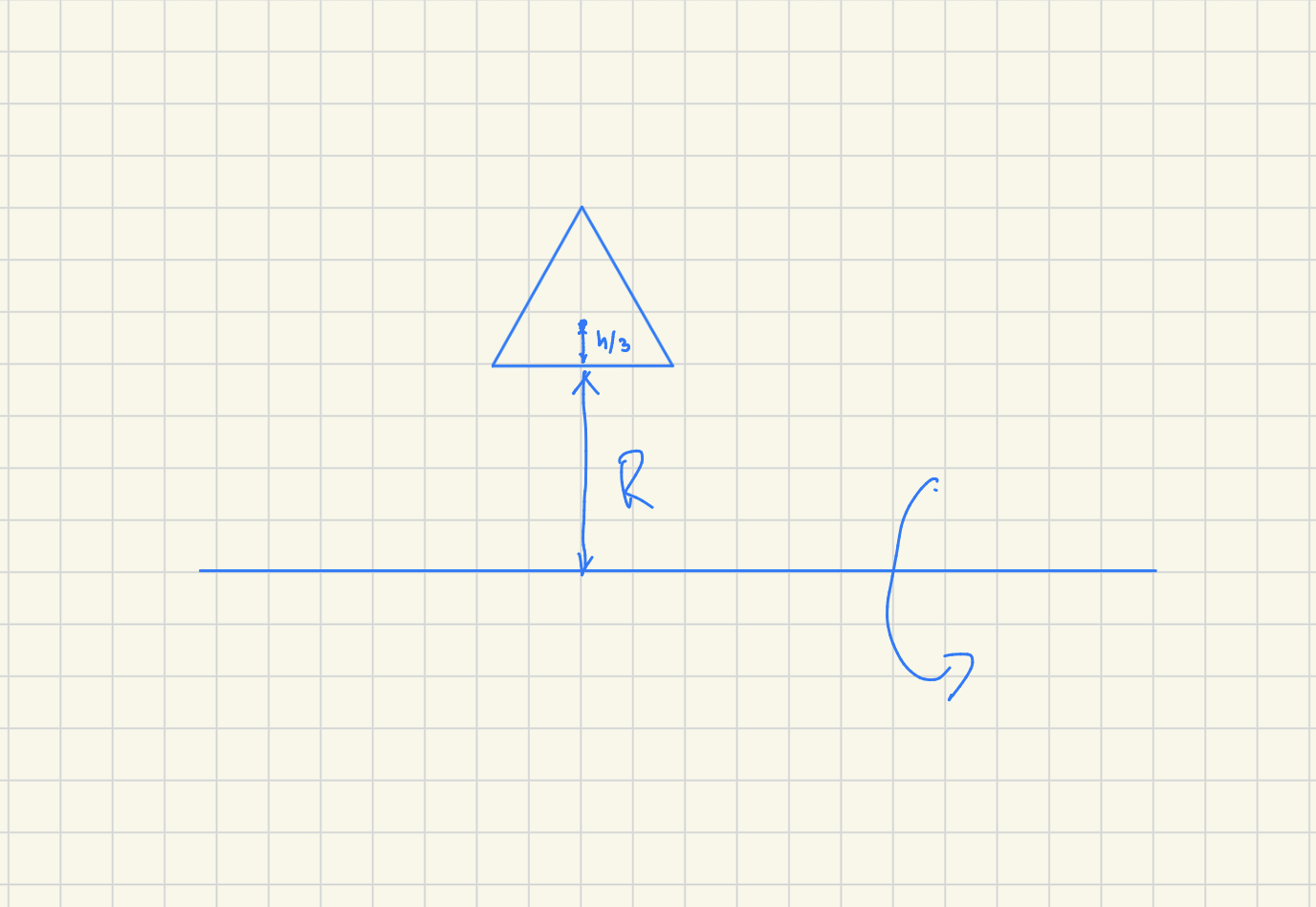
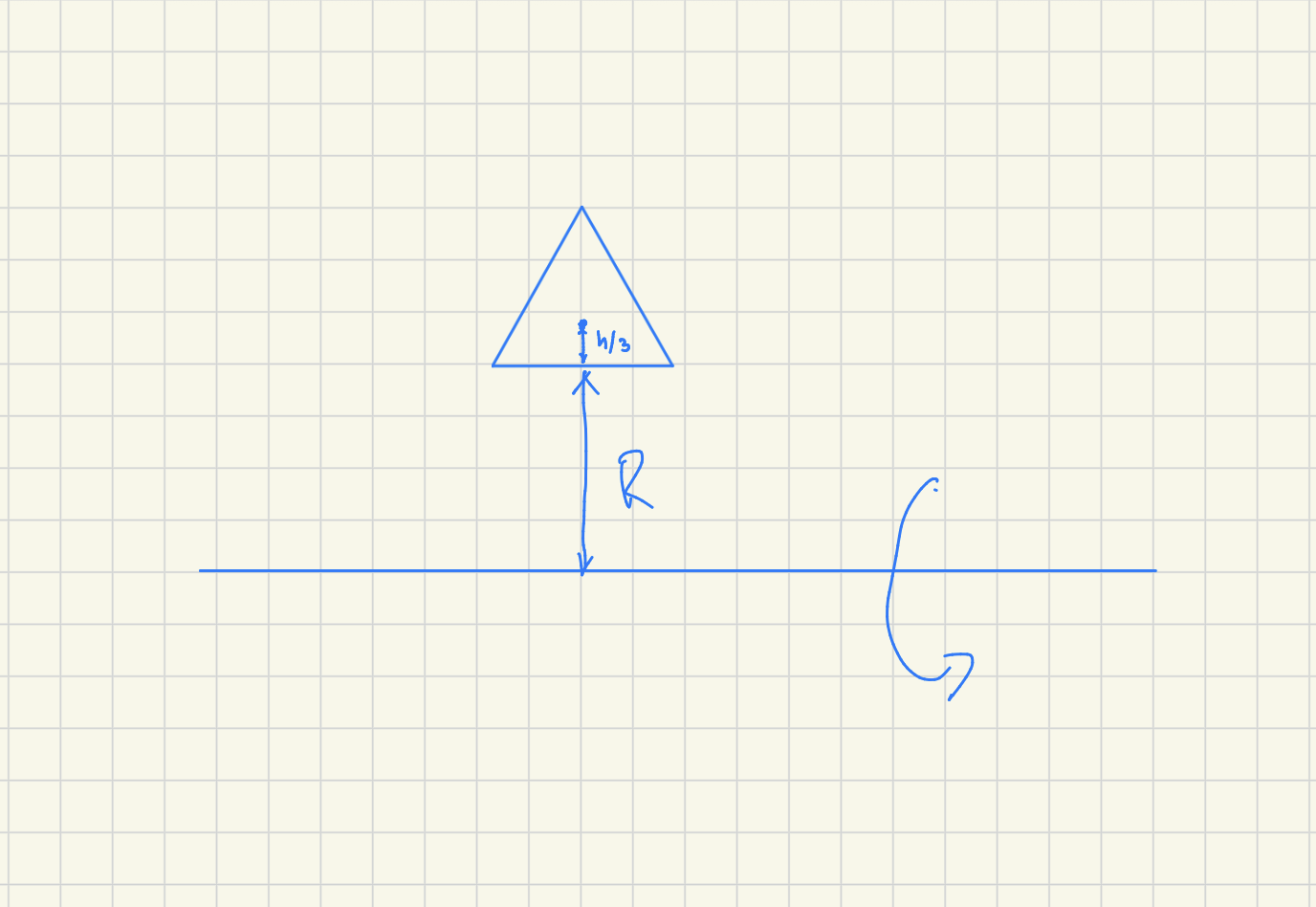
Ja, fast AI-bilden är dålig. Triangelns bas skall ligga på avståndet R från rotationsaxeln, annars får du inte hålrummet i toroidens mitt.
Så tyngdpunktens avstånd till axeln är R + h/3. Sedan får man uttrycka h i termer av a.
PATENTERAMERA skrev:Ja, fast AI-bilden är dålig. Triangelns bas skall ligga på avståndet R från rotationsaxeln, annars får du inte hålrummet i toroidens mitt.
Så tyngdpunktens avstånd till axeln är R + h/3. Sedan får man uttrycka h i termer av a.
Okej men isåfall vet jag inte hur du menar att det ska se ut tyvärr. Jag hänger inte med där. Isåfall är det en sån bild men jag kan ha missförstått dig där.
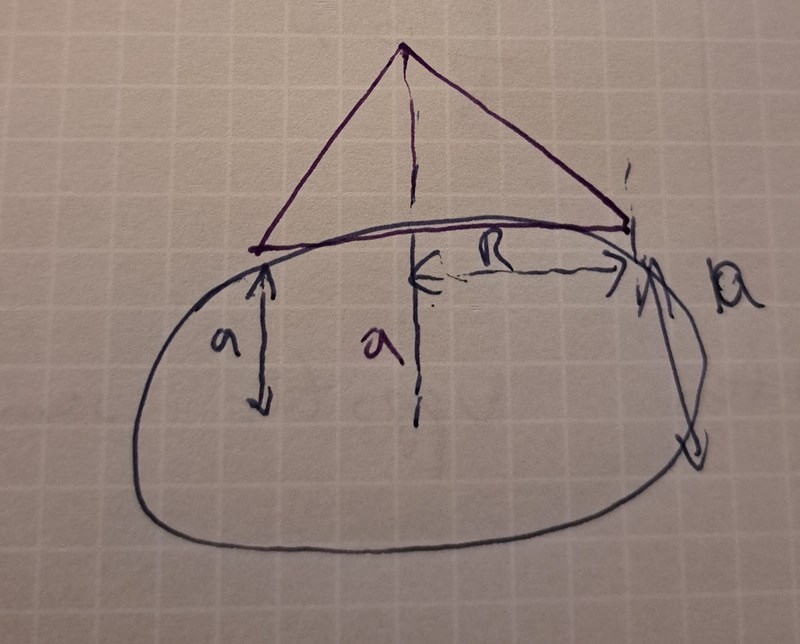
Jag förstår inte och ser inte hur tyngpunktens avstånd till axeln är R+h/3 om figuren från AI eller min egna är fel.
PATENTERAMERA skrev:
Men denna bild verkar ej stämma med hur R ser ut i uppgiften? Är den strecken linjen i mitten av toroiden även R? Så rotationsaxeln för triangeln är mitten av toroiden?
Ja, du roterar kring den horisontella linjen. Då får du toroiden, fast på högkant och inte liggande som i figuren till problemet, men det spelar ju mindre roll.
PATENTERAMERA skrev:Ja, du roterar kring den horisontella linjen. Då får du toroiden, fast på högkant och inte liggande som i figuren till problemet, men det spelar ju mindre roll.
Jag vet inte vilken horisontell linje du syftar på i problemtexten? Du har själv ritat en horisontell linje i din figur, kanske är det den du menar? Vad menar du med högkant?
Ja, den horisontella linjen i min figur. Högkant: den står upp som ett cykelhjul 🚴🏻♀️, istället för att ligga platt ner som en munk 🍩 .
PATENTERAMERA skrev:Ja, den horisontella linjen i min figur. Högkant: den står upp som ett cykelhjul 🚴🏻♀️, istället för att ligga platt ner som en munk 🍩 .
Men du markerade radien där? Vad menas med högkant?
Jag förklarade det i #25.
PATENTERAMERA skrev:
Så på högkant är den horisontell eller om du menar att triangeln står på högkant? Är osäker på vad du försöker säga här.
"På högkant" betyder att något är placerat vertikalt, stående på sin kortsida eller kant istället för att ligga platt.
Så här ser det ut om man skär bort främre halvan av toroiden i första bilden.
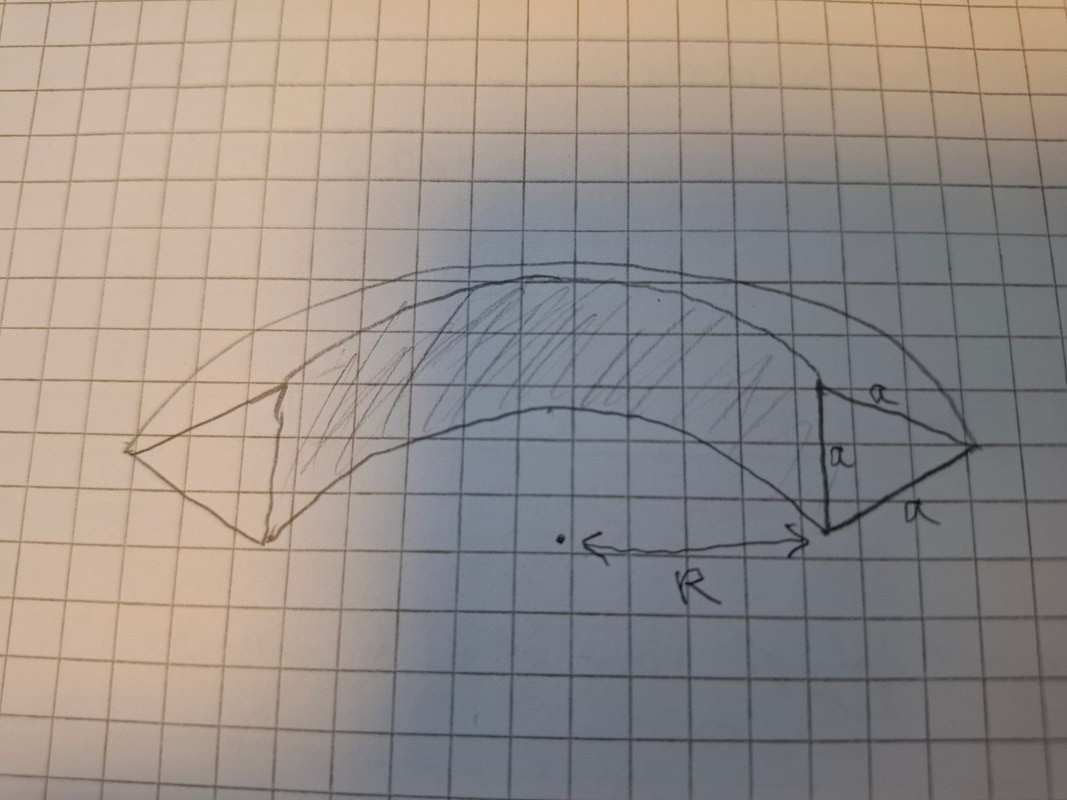
Laguna skrev:Så här ser det ut om man skär bort främre halvan av toroiden i första bilden.
Jaha ok då bildas det en liksidig triangel med sidorna a. Då förstår jag. Så tyngdpunkten på triangeln vid kanten mäts från toroidens rotationsaxel i mitten till mitten av triangeln så vi får R+h/3. För att skriva h i termer av a kan man använda pythagoras sats kanske