Beräkna den markerade arean
"Figuren visar grafen till y = 3sin4x.
Beräkna den markerade arean"
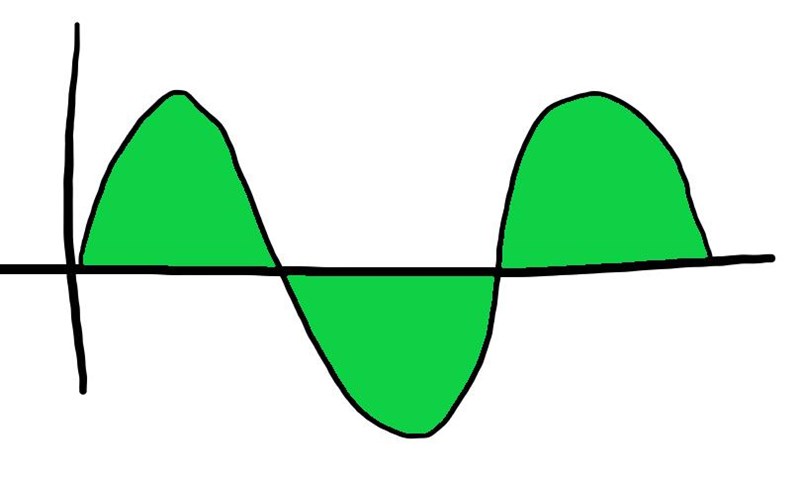
Jag har sökt runt lite på Google och försökt lösa denna i drygt en timme men får inte ut vad jag ska ha för gränsvärden.
Vad jag har just nu är
Hur tar jag reda på a och b?
Vid vilka punkter är funktioner lika med noll? Vid dessa punkter skär ju funktionen -axeln, och detta kan hjälpa dig att klura ut gränserna för området.
a verkar vara 0. Var får du -0.75 ifrån och varför blev det cosinus?
Tydligen ska tre halva perioder vara med. Hur lång är en period för sin(4x)?
Laguna skrev:Hur lång är en period för sin(4x)?
Jag skrev nog tråden lite för snabbt, menade att integralen var och då borde den primitiva funktionen vara -0.75cos4x
LaserLennart skrev:Laguna skrev:Hur lång är en period för sin(4x)?
Jag skrev nog tråden lite för snabbt, menade att integralen var och då borde den primitiva funktionen vara -0.75cos4x
Hej och välkommen till Pluggakuten!
Ja det stämmer.
Då kanske du kan hitta de x-värden där grafen skär x-axeln (dvs funktionens nollställen)?
Som det ser ut nu så fann jag en lösning med ditt förslag, med min primitiva funktion och period (π÷2)
så kunde jag använda enhetscirkeln för att hitta var sinus var 0.
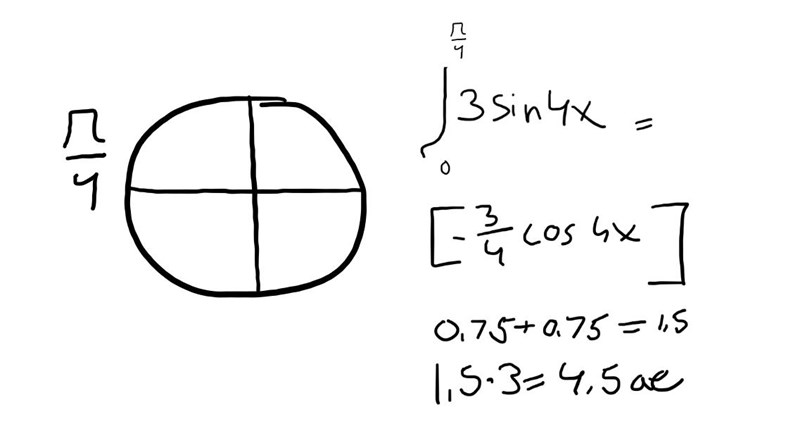
Tack för hjälpen!
Snyggt! Alternativt kan man räkna över alla tre perioderna:
LaserLennart skrev:Som det ser ut nu så fann jag en lösning med ditt förslag, med min primitiva funktion och period (π÷2)
så kunde jag använda enhetscirkeln för att hitta var sinus var 0.
Tack för hjälpen!
Varför tar du 0,75 + 0,75?
Om du räknar ut integralen mellan punkten x = 0 och x = pi/4 borde man inte bara kunna multiplicera svaret med 3 direkt?
Hej och välkommen till Pluggakuten krisse7777!
Jo, det är precis det som LaserLennart gör.
0,75+0,75 kommer av att integralens värde är
3 gånger detta värde blir svaret 4,5.





