Beräkna det maximala värde som förhållandet R/A kan anta.
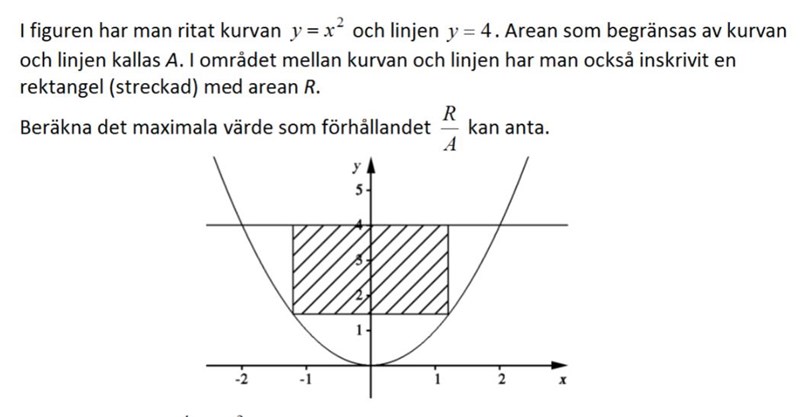
Jag vet att höjden för område A är 4 och att funktionen för kurvan är y =x^2. Då vet jag även att x värdena där kurvan korsar y=4 är -2 och 2. För att räkna ut området "A" integrerar jag x^2. x^3/3 är integralen. genom att använda formeln för integraler räknade jag ut att området blev 16/3 a.e. För att räkna ut R måste jag antagligen räkna ut bxh men jag har inte dessa variabler och jag vet inte riktigt hur jag ska räkna ut någon av dem. Jag vet ju inte vart på y axeln område R börjar eller vart på x axeln den börjar och slutar. Jag har definetivt ingen aning hur jag ska räkna ut det maximala värdet R/A kan anta.
Eller kan jag anta att höjden för område R börjar vid y=1,5?
Det är inte alls säkert att den rektangeln man har ritat upp i bilden är den som ger det största förhållandet!
Området A har en area som kan beräknas med hjälp av en integral.
Ju större rektangeln R:s area är, desto större är förhållandet mellan R och A.
Du vet att två av hörnen på rektangeln ligger på kurvan y=x2 och två ligger på kurvan y=4. Vilka är koordinaterna för de fyra hörnen, om x-värdet för de högra hörnen är x? Vilken area får rektangeln?
Vilken är standardmetoden för att ta reda på nåär något är så stort som möjligt (eller så litet som möjligt)?
jag skulle ju på något sätt vilja sätta att y värdet på rektangelns botten = y2 för att sedan lösa ut x värderna där rektangeln möter kurvan, men det kan jag inte göra. Jag tycker det är så svårt när jag inte riktigt kan anta värden för rektangeln. Standardmetoden för att ta reda på om något är så stort som möjligt är väl att deriva och sätta funktionen lika med noll och ta reda på eventuella maximipunkter.
Du har slarvat när du har räknat ut arean . Den bör bli .
Om vi gör som Smaragdalena föreslår och kallar -koordinaten för rektangelns högra hörn för får vi att hörnen som tangerar kurvan är och . Är du med på det? I så fall, vad blir de andra två hörnen? Kan du då räkna ut rektangelns höjd och bas?
Jag räknade om A och fick nu 32/3 areaenheter. Eftersom jag nu vet rektangels nedersta höjd kordinat är x2 vet jag att höjden är 4-x2. Längden måste bli bli x - (-x) vilket blir 2x. Arean för R måste då bli 2x(4-x2) = 8x-2x3 = 4x - x3. Sedan får jag försöka derivera och ta reda på en maximipunkt. Jag tror jag är på rätt väg nu, tack för hjälpen. Dock så är jag inte helt klar ännu, jag återkommer om jag stöter på ytterligare problem.



