Beräkna en integral med hjälp av trapetsmetoden
Vi har också formeln för trapetsmetoden: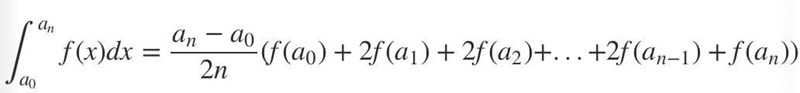
Hur beräknar jag genom trapetsmetoden?
Hur långt kommer du när du använder formeln?
Laguna skrev:Hur långt kommer du när du använder formeln?
n = antal parallelltrapetsar
f(x0), f(x1), f(x2), etc. är längden av parallelltrapetsernas parallella sidor.
Men jag fattar inte vad helheten försöker säga.
Hur mycket är n?
Laguna skrev:Hur mycket är n?
4? I formeln är det an, så det är att vi får an = 4?
Det stämmer.
Om du vet alla värden så sätt in dem i formeln.
Laguna skrev:Det stämmer.
Om du vet alla värden så sätt in dem i formeln.
Så får jag det till. Vet dock inte hur jag ska räkna det som finns innanför uttrycket?
Det finns en tabell i uppgiften som berättar vad f(x) är för x = 0, 1, 2, 3 och 4.
Smaragdalena skrev:Det finns en tabell i uppgiften som berättar vad f(x) är för x = 0, 1, 2, 3 och 4.

Såhär har de räknat ut det. Hur fungerar det? Varför är övre gränsen 1, och nedre 0?
Övre gränsen 1 verkar vara ett skrivfel.
Laguna skrev:Övre gränsen 1 verkar vara ett skrivfel.
Vilket är samma sak som:
Skulle du säga att detta är rätt sätt att skriva det på?
Dani163 skrev:Laguna skrev:Övre gränsen 1 verkar vara ett skrivfel.
Vilket är samma sak som:
Skulle du säga att detta är rätt sätt att skriva det på?
Bump
Jämför med de andra formlerna. Du ska inte ha en faktor 2 framför -0,1. Det märker du om du räknar ut och jämför med det rätta svaret.
Om det är rätt sätt att skriva på är inte så noga så länge det är korrekt, det är bara ett mellanresultat.



