Beräkna flödet av vektorfältet ut ur området
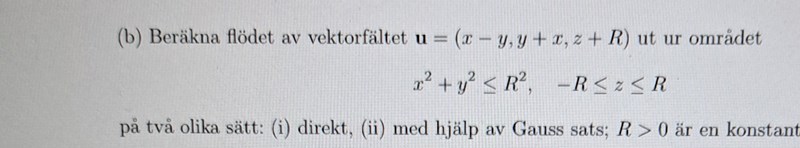


Hej!
Rätt svar ska vara 6piR^3 när man beräknar flödet direkt utan gaus lag. Jag vet inte vad jag har gjort för fel eller vad jag missat här. Sen skulle jag behöva ledtråd i b) uppgiften!
R är en konstant här. Dina variabler är z och .
Sedan måste du även räkna ut flödet genom topp och botten av cylindern.
PATENTERAMERA skrev:R är en konstant här. Dina variabler är z och .
Sedan måste du även räkna ut flödet genom topp och botten av cylindern.
Menar du att min parametrisering är fel eller vad ska jag ändra på i min lösning?
Ja, du skall använda z som parameter istället för R. R är bara en given konstant.
PATENTERAMERA skrev:Ja, du skall använda z som parameter istället för R. R är bara en given konstant.
Ok hur vet vi att R är konstant?
Det står uttryckligen i problemtexten.
PATENTERAMERA skrev:Det står uttryckligen i problemtexten.
Aa ok. Jag får att integralen blir 0 här . Vad är felet? Vilket flöde är det som jag beräknar nu?


Du skall inte ta bort R i dina formler. r = (Rcos(theta), Rsin(theta), z).
Sedan måste du tänka på vilket tecken du skall ha på din normal. Eftersom du skall räkna ut flödet ut ur området så skall du ha en utåtriktad normalriktning.
PATENTERAMERA skrev:Du skall inte ta bort R i dina formler. r = (Rcos(theta), Rsin(theta), z).
Sedan måste du tänka på vilket tecken du skall ha på din normal. Eftersom du skall räkna ut flödet ut ur området så skall du ha en utåtriktad normalriktning.
Men du sa innan att R är konstant. Så jag förstår inte riktigt hur jag ska ändra parametrisering.
Ja, R är en konstant.
PATENTERAMERA skrev:Ja, R är en konstant.


Nu stämmer det väl? Detta är alltså flödet av mantelytan?
Ja, nu tror jag det blev rätt. Sedan är topp och botten kvar.


