Beräkna följande generaliserade integral eller visa att den divergerar

Vad ska det stå i täljaren?

Är det $\arctan x$ ?

Ett knep är att dela upp integralen i två intervall:

$[0,1]$ och $[1,\infty]$.

Tack för jätte snabbt svar tomast80! Jag ska åka och jobba nu kollar upp dina tips när jag kommer hem igen :) 

Den är bara generaliserad i en punkt (ser du varför?) så den borde inte behöva delas upp.

Nämnaren är ganska lik täljarens derivata, så jag skulle testa med partiell integration.

Riktigt jobbig integral men det finns en primitiv funktion. Substituera x = tan u.

Micimacko skrev:

Den är bara generaliserad i en punkt (ser du varför?) så den borde inte behöva delas upp.

Nämnaren är ganska lik täljarens derivata, så jag skulle testa med partiell integration.

$x=\frac{\pi}{2}$ ?

Kan man inte bara direkt konstatera att:

$\displaystyle \int_0^{\infty} \frac{\arctan x}{(1+x^2)^{3/2}}dx<$
$\displaystyle \int_0^{\infty} \frac{\arctan x}{1+x^2}dx=$
...

Vad händer när x=pi/2??

Micimacko skrev:

Vad händer när x=pi/2??

Inget speciellt, jag tänkte fel. Men då kan man väl endast konstatera att

integralen < $\lim_{x\to \infty} [\frac{(\arctan(x))^2}{2}]_0^x=\frac{(\pi/2)^2}{2}=...$ ?

Ja första delen är lätt. Jag hade bara avrundat arctan till pi/2 och strukit ettan i nämnaren.

Micimacko skrev:

Ja första delen är lätt. Jag hade bara avrundat arctan till pi/2 och strukit ettan i nämnaren.

Vilken del är det som inte är lätt, med ovanstående är man väl klar? 🤔

Det står beräkna integralen också.

Micimacko skrev:

Det står beräkna integralen också.

Ja, det står så i uppgiften, men skulle gärna vilja se en bild på uppgiften. I 99 fall av 100 ska man endast avgöra om den är konvergent eller divergent.

Om man substituerar u = arctanx <=> x = tanu så kan man beräkna integralen.

Det stämmer..

Substituera u =arctanx  du= 1/1+x²dx 

och fortsätt lösa..

I uppgiften står det exakt: Beräkna följande generaliserade integral eller visa att den divergerar. Så jag antar att man kan välja om man vill lösa generaliserade integral eller visa att den divergerar, så frågan är bara vad man tycker är lättast/bäst. 

Det är ingen fri vilja inblandad här, antingen så divergerar den (och går då inte räkna ut) eller så gör den inte det.

Okej, tack Micimacko. Jag har börjat som du sa att avrunda arctan till pi/2 samt stuckit ettan i nämnaren. 

viktoria10 skrev:

I uppgiften står det exakt: Beräkna följande generaliserade integral eller visa att den divergerar. Så jag antar att man kan välja om man vill lösa generaliserade integral eller visa att den divergerar, så frågan är bara vad man tycker är lättast/bäst. 

Som jag misstänkte, då kan man ersätta $\frac{3}{2}$ med $1$ och sedan räkna ut (den enklare) integralen.

Vad menar du tomas? Det står ju att den ska beräknas?

Testa variabelbytet som föreslagits ett par inlägg upp.

Jag förstod inte heller, tomast80. 

Micimacko skrev:

Vad menar du tomas? Det står ju att den ska beräknas?

Testa variabelbytet som föreslagits ett par inlägg upp.

Jag blev nog förvirrad av att byta ut $\arctan x$ mot $\frac{\pi}{2}$.
Men håller med, lös integralen medelst variabelsubstitution.

Jag har fått många olika tips! Tack allesammans! Jag försöker att börja lösa uppgiften nu. Och kommit fram till detta med eran hjälp. 

${\int }_0^{\infty }\frac{arc\tan }{{(1+x^2)}^{(3/2)}}dx = \frac{\mathrm{\pi }/2}{{\left(x^2\right)}^{(3/2)}} dx$

Sen substituerar jag u = arctanx <=> x = tanu:

$\frac{\mathrm{\pi }/2}{\left(\tan \right(arc\tan {{\left(x\right))}^2}^{(3/2)}}$= $\frac{\mathrm{\pi }}{2x^3}$

Derivatet av funktionen är:

-$\frac{3\mathrm{\pi }}{2\left(x^4\right)}$

Vad är det du försöker göra nu?

Jag försökte göra det som Henrikus sa "Om man substituerar u = arctanx <=> x = tanu så kan man beräkna integralen." 

Jo men du bytte integral, det är den i uppgiften du ska räkna ut.

Jaha okej, jag måste ha uppfattat det fel. Känner mig väldigt osäker på det här. Jag uppfatta det som att ${\int }_0^{\infty }\frac{arc\tan }{{(1+x^2)}^{(3/2)}} dx$=${\int }_0^{\infty }\frac{\mathrm{\pi }}{2x^3} dx$.

Eftersom jag bytte ut arctan mot pi/2 samt tog bort ettan som du sa. Sen substituerar jag u = arctanx  och x = tanu. 

Det är 2 olika delar i en typisk lösning när man har en generaliserad integral.

Först vill du avgöra om den går att räkna ut. Det brukar man göra genom att avrunda uppåt på olika sätt. Sen får man då tex pi/2x^(6/2). Den behöver inte räknas ut, det räcker att titta på och säga att det går.

Då går den mindre vi hade från början också att räkna ut. Och där börjar del 2 av lösningen, att se vad det blir. Då får du inte avrunda som du vill, utan använda exakt det du fick för att svaret ska bli rätt.

Okej, tack. Jag försöker igen :)

okej, så vi kan snabbt konstatera att den här intergralen går att lösa, genom det du tidigare nämnde "Jag hade bara avrundat arctan till pi/2 och strukit ettan i nämnaren." 

Ska jag efter det då gå tillbaka ursprungs integralet och göra som henrikus sa "u = arctanx <=> x = tanu så kan man beräkna integralen."? 

Det som gör mig mest förvirrad är att det bara står arctan och inte arctan(x) eller något likande i täljaren. 

Det ska nog stå arctanx, jag hade nog bara kört partiell integration, men prova substitutionen du har blivit tipsad om flertal gånger i tråden. 

Okej jag tror jag börjar förstå substitution mer nu. Det är första gången jag använder det. 

Så jag skriver som arc tan(x)= u :

$\frac{u}{{(1+x^2)}^{(3/2)}} dx$

och du är = $\frac{1}{x^2+1}$dx

dvs nästan samma uttryck som i nämnaren förutom ^(3/2). 

Brukar man inte sen ta bort du? men kan jag göra det när ^(3/2) finns kvar?

Blir det såhär eller är jag helt fel ute?

$\frac{u+1}{{\left(du\right)}^{(3/2)}}$

Det ser inte riktigt ut.
u=atan(x) ger att x=tanu.
du=1/(x^2+1) dx <=> dx = du (x^2+1). notera att gränserna blir från 0 till pi/2. du har då $\displaystyle{\int_0^{\pi /2} \frac{u}{(( \tan u )^2+1)^{(1/2)}}dx}$ och eftersom sec^2(x)-tan^2(x)=1 får du $\displaystyle{\int_0^{\pi /2} \frac{u}{\sec (u)}du}$

Kommer du vidare?

När jag ser din uträkning får jag fram detta: $u\times \mathrm{\pi }/2\sec \left(\mathrm{u}\right)$.

Tidigare när jag försökte räkna ut integralen kom jag fram till: -1 $\frac{\mathrm{\pi }}{2}$. 

Jag har för mig att det blir $\frac{\pi}{2}-1$, så har du redan fått det så har du ju räknat klar.

Då blev det rätt då. Men jag känner mig fortfarande osäker på hela processen att komma dit eftersom det finns många vägar. Nu löste jag det med hjälp av kurs litteraturen och var osäker under processen :( tänker att jag ska försöka träna på den metoden där man använder substitution som ni föreslog. Vill kunna skriva och uttrycka lösningen på ett snyggt sätt, det som jag löste löste nu själv var inte optimalt om man säger det så. 

Tror att enda sättet att lära sig integrera mer säkert är att träna på väldigt många olika uppgifter. Finns hur mkt som helst på yt, bara att försöka själv först och sen jämföra med hur de gör i videon.

Tack för tipset Micimacko. Det är väl bästa metoden nu när universiteten är stängda. Tack för all hjälp allihopa! :)

Hej,

Jag ser att ni har fått fram pi/2-1. Men jag undrar; ska man också får fram det andra talet som ekvationen konvergerar emot?

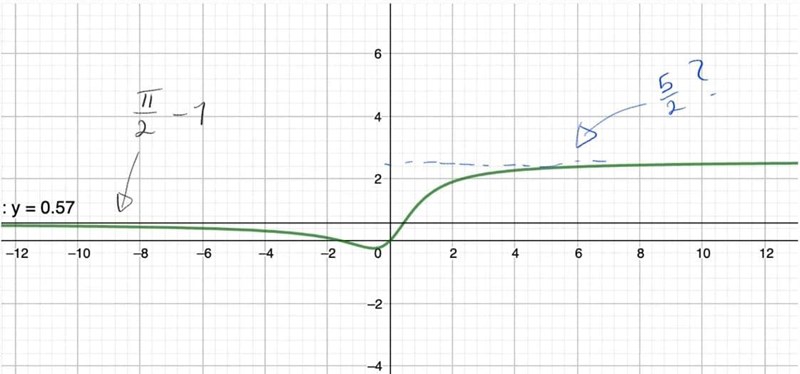
Caroline.E skrev:

Hej,

Jag ser att ni har fått fram pi/2-1. Men jag undrar; ska man också får fram det andra talet som ekvationen konvergerar emot?

Vilket andra tal och vilken funktion? (ekvationer brukar inte konvergera) Arctan är udda och nämnaren jämn, så ser inte sådär direkt hur du skulle få fram något annat.

Hej,

När jag kollar upp funktionen på geogebra så ser den ut som på bilden. Har inte den blå streckade linjen någon betydelse när vi ska ta reda på om funktionen konvergerar? Jag är ny på detta, så jag kanske missar något. (Som tex att grafen är jämn eller att arctan bara är positiv?)

Vänligen 
Caroline 

Kan du visa vad du har skrivit in?

Hej, 

Oj, jag måste ha skrivit in fel. Förlåt.

Nu får jag den här grafen.

Vänligen 

Caroline 

Då var det ingenting, antar jag. :) 

Vet inte vad du skulle få ut av grafen oavsett. Förstår du vad de frågar efter?

Ne, det har du rätt i, märker jag nu i efterhand. Antar att dom vill ha arean som integralen konvergerar till och inte värdet funktionen konvergerar till. Om jag uttrycker mig rätt. 

Ja, det låter bättre 😉

Dracaena skrev:

Det ser inte riktigt ut.
u=atan(x) ger att x=tanu.
du=1/(x^2+1) dx <=> dx = du (x^2+1). notera att gränserna blir från 0 till pi/2. du har då $\displaystyle{\int_0^{\pi /2} \frac{u}{(( \tan u )^2+1)^{(1/2)}}dx}$ och eftersom sec^2(x)-tan^2(x)=1 får du $\displaystyle{\int_0^{\pi /2} \frac{u}{\sec (u)}du}$

Kommer du vidare?

Hej, 

Hur tar du steget mellan

${\int }_0^{\pi /2}\frac{u}{\left(\right(\tan u{)}^2+1{)}^{(1/2)}}dx$

och 

${\int }_0^{\pi /2}\frac{u}{\sec \left(u\right)}du$

Vänligen

Caroline 

Caroline.E skrev:

Dracaena skrev:

Det ser inte riktigt ut.
u=atan(x) ger att x=tanu.
du=1/(x^2+1) dx <=> dx = du (x^2+1). notera att gränserna blir från 0 till pi/2. du har då $\displaystyle{\int_0^{\pi /2} \frac{u}{(( \tan u )^2+1)^{(1/2)}}dx}$ och eftersom sec^2(x)-tan^2(x)=1 får du $\displaystyle{\int_0^{\pi /2} \frac{u}{\sec (u)}du}$

Kommer du vidare?

Hej, 

 

Hur tar du steget mellan

${\int }_0^{\pi /2}\frac{u}{\left(\right(\tan u{)}^2+1{)}^{(1/2)}}dx$

 

och 

${\int }_0^{\pi /2}\frac{u}{\sec \left(u\right)}du$

 

Vänligen

Caroline 

Det är steget här ${\int }_0^{\pi /2}\frac{u}{\left(\right(\tan u{)}^2+1{)}^{(1/2)}}\times \left(\right(\tan u{)}^2+1)du$

Jag inte kommer underfund med..

Nej,

Nu ser jag.. ^2 tar ut rottecknet. 

Hur kommer vi fram till dom nya gränserna 0 - pi/2?

Vi har att $u= \arctan (x)$, om x går mot oändligheten går atan(x) mot pi/2 och om x går mot 0 går atan(x) också not noll. Vi får då gränserna till 0 till pi/2.