Beräkna fyrhörningens area

uppgfiten lyder som följande:

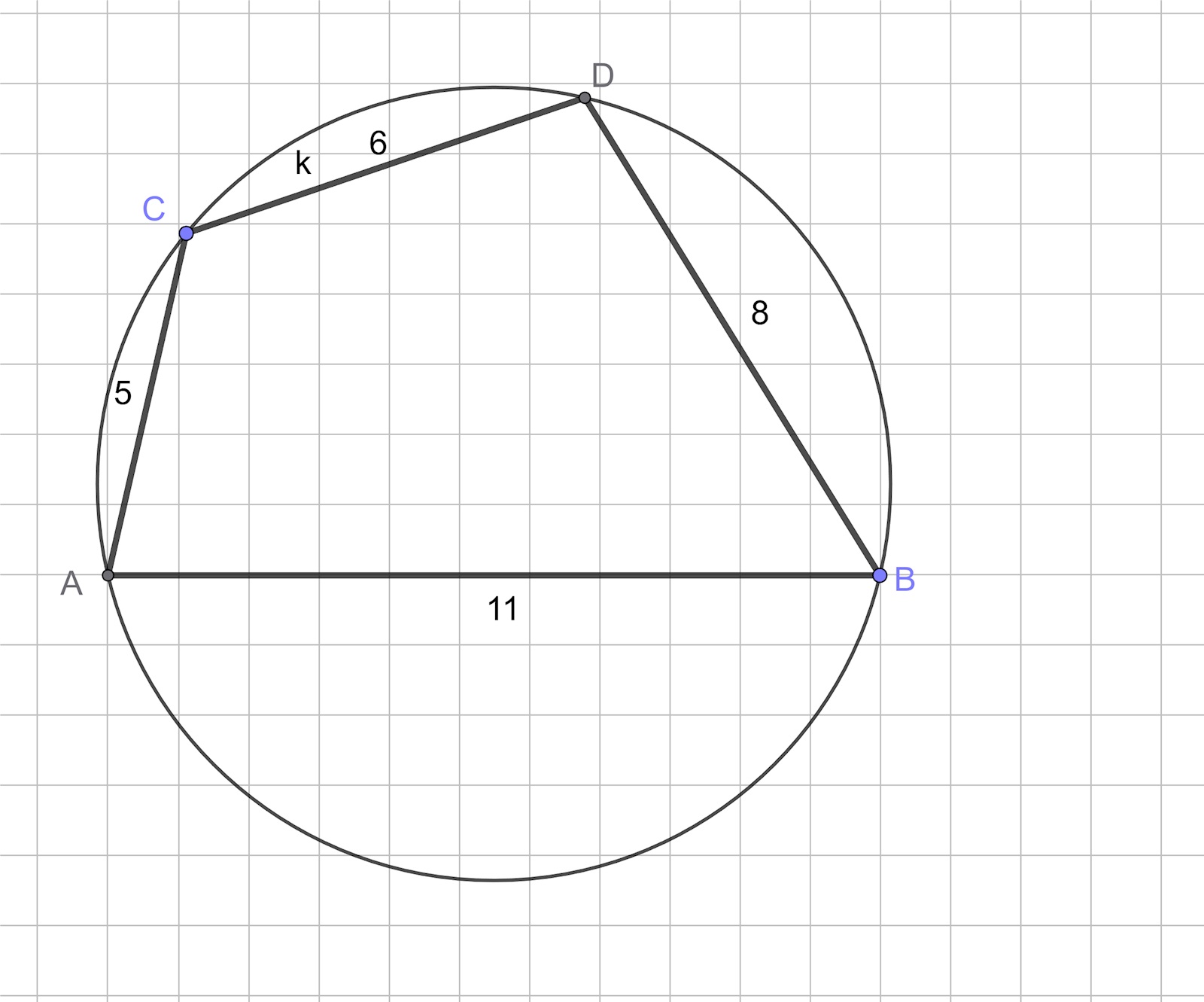
En fyrhörning med sidorna 5, 6, 8 och 11 cm är inskriven i en cirkel. Beräknafyrhörningens area.

Förstår inte hur jag ska göra.

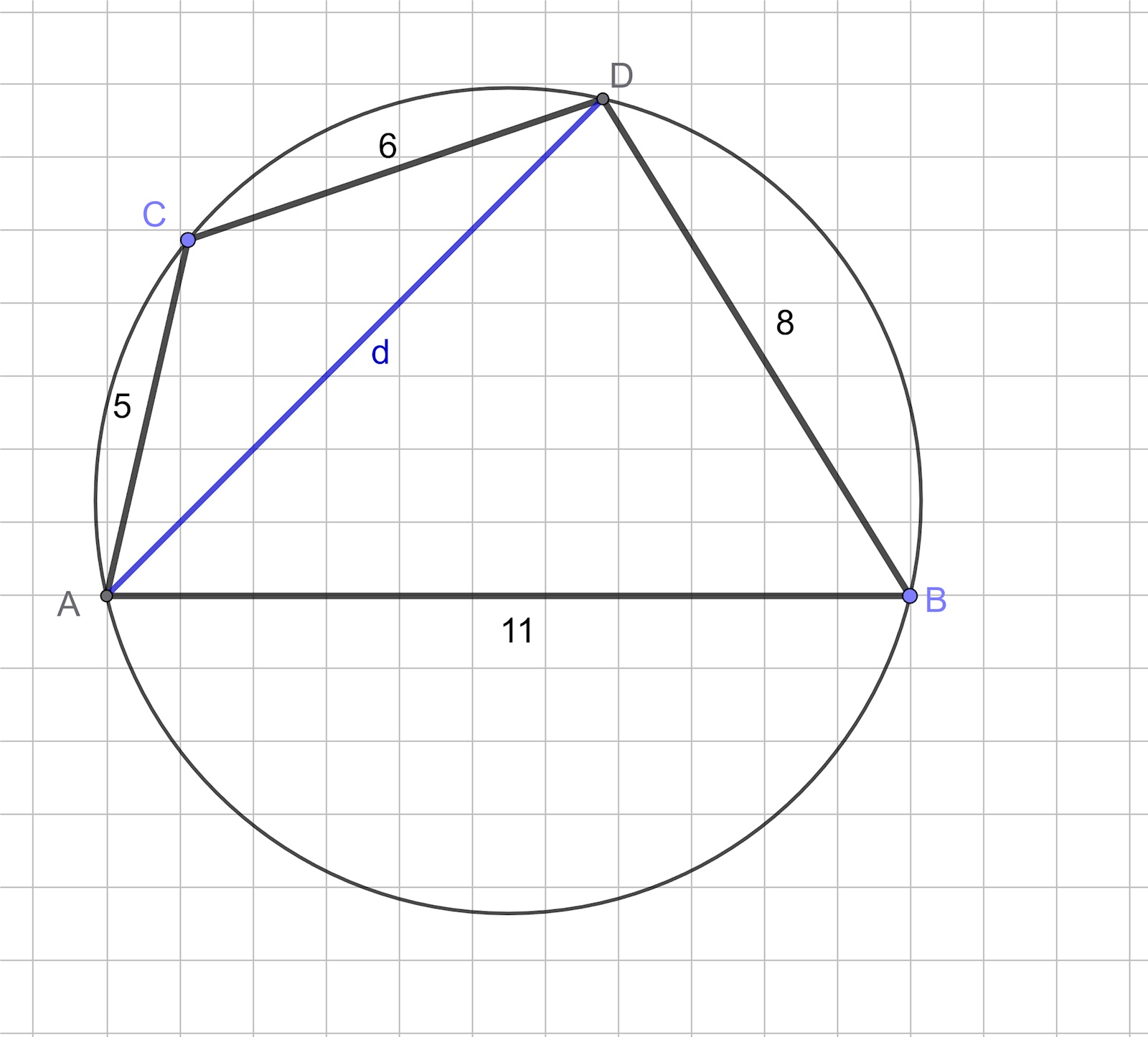
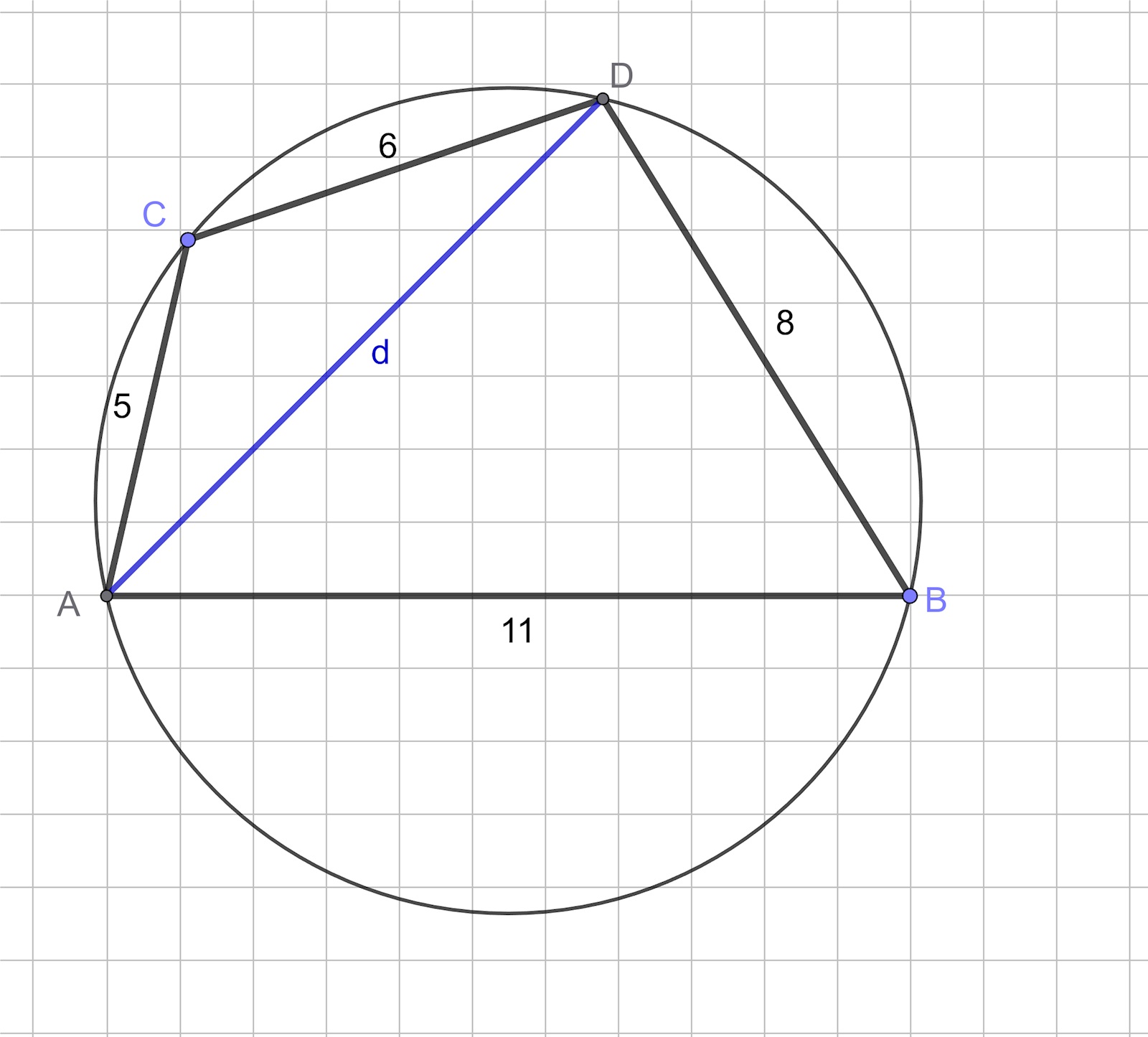
Så här långt har jag kommit. jag har ritat en figur, och tänkte att randvinkelsatsen kanske ska användas i kombination med cosinussatsen för att räkna diagonalen som dividerar fyrhörningen till 2 trianglar. Men om jag kallar ena vinkeln för v blir den andra 180 - v. sen kan jag inte använda cosinus för att lösa linjen som delar fyrhörningen i 2 trianglars längd

https://www.pluggakuten.se/trad/triangelsatserna-5/

Magnus O skrev:
https://www.pluggakuten.se/trad/triangelsatserna-5/

Jag förstår inte svaret.

$d^2 = 5^2 + 6^2 - 2\cdot 5 \cdot 6 \cdot \cos{\angle C}$

$d^2 = 11^2 + 8^2 - 2 \cdot 8 \cdot 11 \cdot \cos {\angle B}$

$5^2 + 6^2 - 2 \cdot 5 \cdot 6 \cos{\angle C} = 11^2 + 8^2 - 2 \cdot 8 \cdot 11 \cdot \cos{(180^o - \angle C)}$

MaKe skrev:

$d^2 = 5^2 + 6^2 - 2\cdot 5 \cdot 6 \cdot \cos{\angle C}$

$d^2 = 11^2 + 8^2 - 2 \cdot 8 \cdot 11 \cdot \cos {\angle B}$

$5^2 + 6^2 - 2 \cdot 5 \cdot 6 \cos{\angle C} = 11^2 + 8^2 - 2 \cdot 8 \cdot 11 \cdot \cos{(180^o - \angle C)}$

25 + 36 - 60cos(vinkeln C) = 121 + 64 - 176cos(180-C)

-60cos(vinkel C)=124 - 176cos(180-c)

Jag fastnar här.

cos(vinkel C) är jue inte samma cos(180-c)

Nej, men cos (a)=-cos(180-a) som ger cos a ur ekvationen, och därmed sin a

Sen kan man använda sinussatsen för yta på trianglarna ACD och ABD tex

Y = 5*6 sin a /2 + 11*8 sin (180-a)/2 (sin a = sin 180 -a)

Svara

Visa senaste svar