Beräkna g som genereras av cylindersymmetriska masstätheten

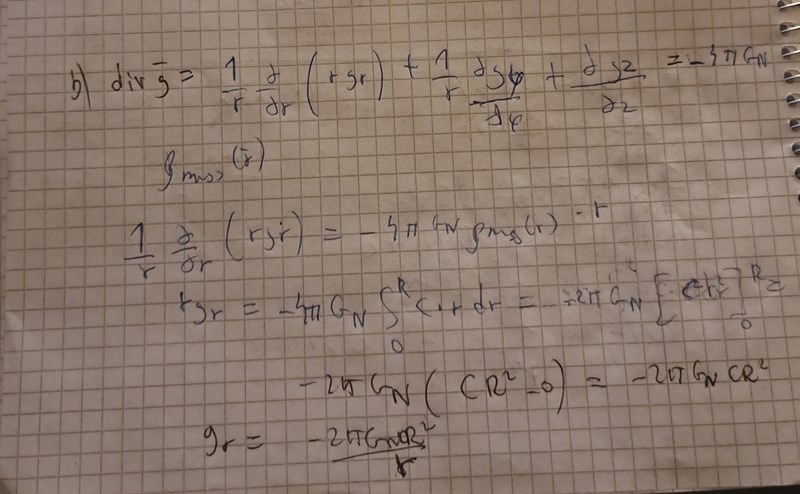
Facit fick två olika svar på vad g kan vara. Hur ska man tänka här? Jag fick bara ett svar på g(r)
Anyone?
Du måste behandla fallen att r R och r > R separat.
I) r R:
rgr = .
II) r > R
rgr = .
PATENTERAMERA skrev:Du måste behandla fallen att r R och r > R separat.
I) r R:
rgr = .
II) r > R
rgr = .
Varför behandla dem separat?
Generellt
rgr = .
Om r mindre än eller lika med R
rgr = .
Om r större än R
rgr = .
PATENTERAMERA skrev:Generellt
rgr = .
Om r mindre än eller lika med R
rgr = .
Om r större än R
rgr = .
Hänger tyvärr inte med. Om r>=R , borde det inte vara gränserna 0 till r ? Den andra delen förstår jag inte riktigt.
För r > R delar du upp integralen från 0 till r i två delar: först från 0 till R (rho = C här) och sedan från R till r (rho = 0 här). Inga konstigheter.
PATENTERAMERA skrev:För r > R delar du upp integralen från 0 till r i två delar: först från 0 till R (rho = C här) och sedan från R till r (rho = 0 här). Inga konstigheter.
Alltså det är faktiskt konstigheter för jag förstår inte varför r>R innebär 0 till r i två delar? Sen är jag även förvirrad över om det är r eller R som utgör gränserna.
Eftersom densiteten har olika värden mellan 0 och R (C) och mellan R och r (0). Inga konstigheter.
Om du har en funktion f som definierad så att f(x) = h(x) då x ligger mellan a och b och så att f(x) = h(x) då x ligger mellan b och c hur skulle du beräkna integralen
?
PATENTERAMERA skrev:Eftersom densiteten har olika värden mellan 0 och R (C) och mellan R och r (0). Inga konstigheter.
Om du har en funktion f som definierad så att f(x) = h(x) då x ligger mellan a och b och så att f(x) = h(x) då x ligger mellan b och c hur skulle du beräkna integralen
?
så rho(r)=C då r<=R och rho(r)=0 då r>R vilket innebär att från 0 till R så är rho(r)=C och rho(r)=0 då r ligger mellan 0 och R. Jag ser dock inte likheten mellan din exempelfunktion och uppgiften.
Enligt integral regler så är det väl såhär det gäller:
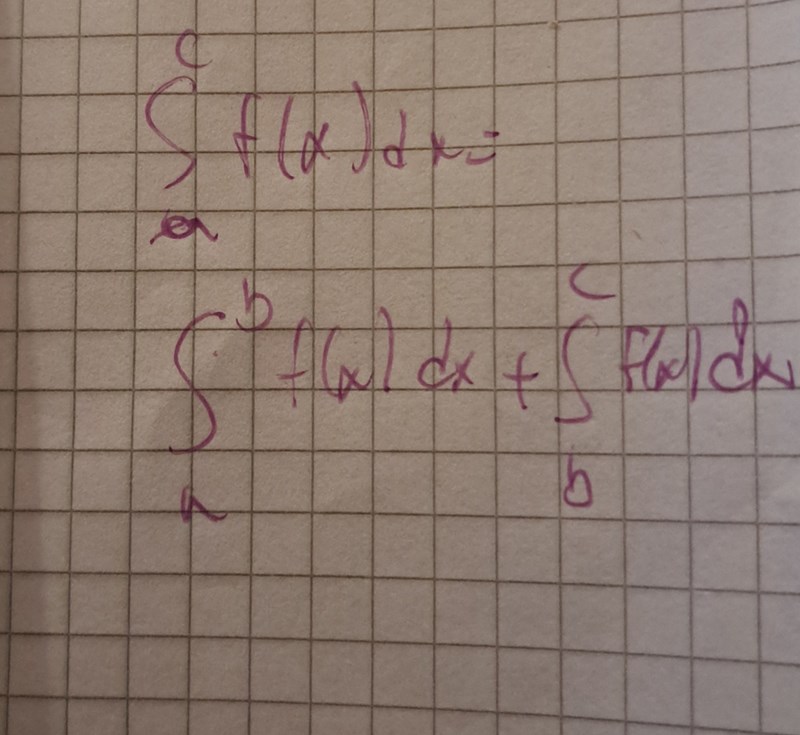
Haha, jag menade att f(x) = g(x) mellan b och c. Så att vi sätter f(x) = h(x) i första integralen och f(x) = g(x) i andra integralen.
PATENTERAMERA skrev:Haha, jag menade att f(x) = g(x) mellan b och c. Så att vi sätter f(x) = h(x) i första integralen och f(x) = g(x) i andra integralen.
Menar du såhär då?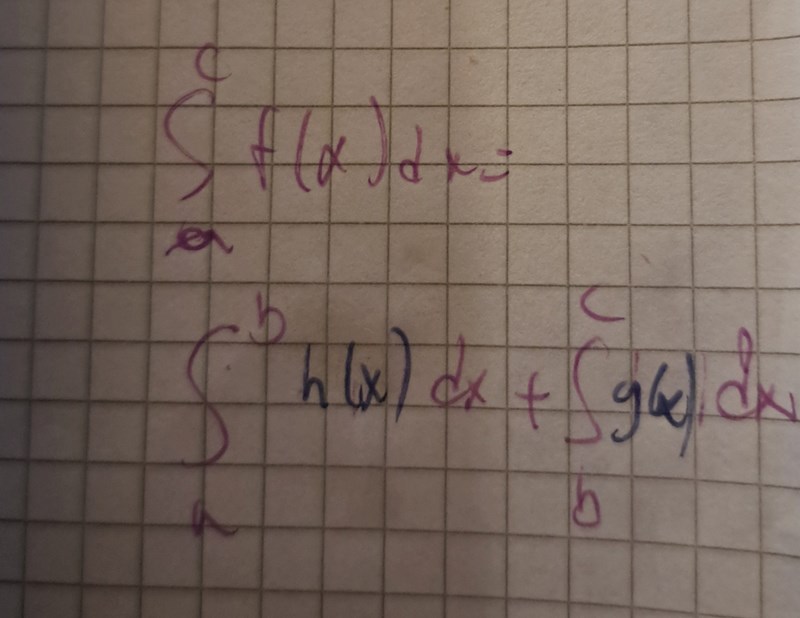
Ja, precis.
PATENTERAMERA skrev:Ja, precis.
Ok i vårt fall, hur kan vi relatera detta till vår uppgift ? Jag ser inte sambandet tyvärr.
rho(r) = C mellan 0 och R. rho(r) = 0 mellan R och oändlighet.
PATENTERAMERA skrev:rho(r) = C mellan 0 och R. rho(r) = 0 mellan R och oändlighet.
Jaha ok då är jag med. lilla r är alltså integrationsvariabel.
PATENTERAMERA skrev:Ja.
Men då har vi bara kvar -4piGCr integralen som är mellan 0 till r då den andra blir 0 dvs R till oändlighet. g(r) kommer då vara det jag fått i #1 samt 0
Ja, för r större än R.
För r mindre än eller lika med R så varierar gr linjärt med r.
Typ någonting i stil med
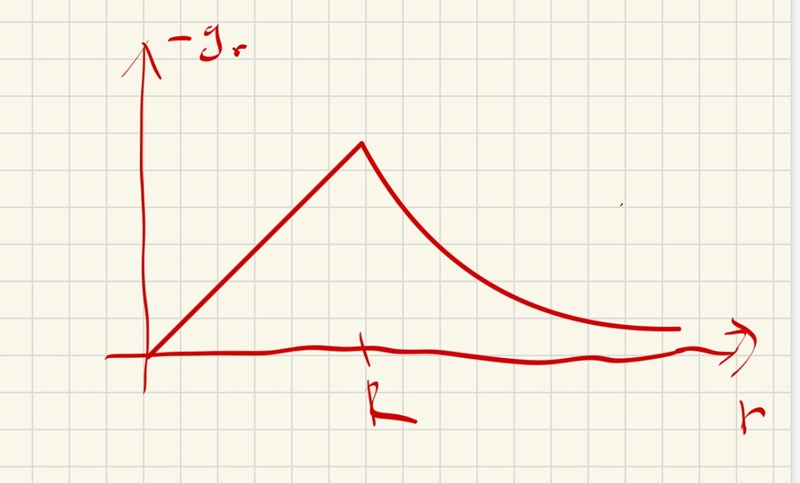
PATENTERAMERA skrev:Ja, för r större än R.
För r mindre än eller lika med R så varierar gr linjärt med r.
Typ någonting i stil med
Ja för r<=R så får vi ju det här svaret -2piGNR2/r , men för r>R så borde g(r) 0 i intervallet (R, inf). Men facit fick något svar som -2piGN/r och det förstår jag inte.
Nja, för r <= R så får du gr = -kr. Där k är en konstant.
För r > R får du gr = -k’/r. Där k’ är en konstant.
PATENTERAMERA skrev:Nja, för r <= R så får du gr = -kr. Där k är en konstant.
För r > R får du gr = -k’/r. Där k’ är en konstant.
Nu hänger jag inte alls med. För r<=R så är g(r)=-kr där k =-4piGNC men det andra förstår jag inte alls..
Vi har att (då r > R)
rgr = = -2(pi)CR2.
gr = -2(pi)CR2/r = -k’/r. (k’ = 2(pi)CR2).
PATENTERAMERA skrev:Vi har att (då r > R)
rgr = = -2(pi)CR2.
gr = -2(pi)CR2/r = -k’/r. (k’ = 2(pi)CR2).
Den sista raden förstår jag inte. Det ska väl vara gr=-2piCR2/r som svar för r<=R? jag kan säga att för r>=R är mitt svar korrekt men facit har en till svar på detta också , nämligen -2piCR/r och där vet jag inte varför och det gäller för r>R. Innan sa du även att r>R är fram R till inf och integranden blir 0 i det intervallet, men nu är jag ganska förvirrad då vi tittar på 0 =>R istället ? Har vi inte gjort en gång för r<=R?
Nej, det är för r > R.
För r <= R så är gr = -2(pi)Cr = -kr.
PATENTERAMERA skrev:Nej, det är för r > R.
För r <= R så är gr = -2(pi)Cr = -kr.
Jag tror inte jag förstår hur man räknar på detta samt varför det ser ut som det gör. Jag fick ju enligt min uträkning -2piGNCR2/r i #1 och tog för givet att det var just mellan 0 till R då r<=R , men då säger du att det är istället för r>R och jag förstår inte varför.
Se #5.
PATENTERAMERA skrev:Se #5.
Jag förstår den inte heller.
Var tappar vi dig?
PATENTERAMERA skrev:Var tappar vi dig?
Jag är bara med på uttrycket för att integrera mellan 0 till R i intervallet (0,R) (r <=R)vilket ger precis jag fått i #1. Men det som handlar om r>R är jag inte med på för du gör en integral uppdelning som inte är logiskt. Jag trodde r>R =(R,inf).
Nej. Det gäller alltid att
rgr = .
Om r <= R.
Om r > R
PATENTERAMERA skrev:Nej. Det gäller alltid att
rgr = .
Om r <= R.
Om r > R
Jag förstår inte riktigt. Vi har gränserna 0 till r istället för 0 till R för fallet r<=R vilket är super förvirrande när r är integrationsvariabel. Det andra fallet förstår jag inte alls mig på den hur mycket du än integrerar för där tycker jag att det borde vara 0 som uppgiften säger. Annars vet jag inte hur man ska se på detta.
Ja om man skulle vara petig så skulle man kalla integrationsvariabeln något annat.
Tex
rgr(r) = . Men ofta är man lite slarvig/lat.
PATENTERAMERA skrev:Ja om man skulle vara petig så skulle man kalla integrationsvariabeln något annat.
Tex
rgr(r) = . Men ofta är man lite slarvig/lat.
Jag förstår fortfarande inte båda fall enligt allt jag skrev i #33.
Sov på saken. Kom tillbaka om det inte klarnar.
PATENTERAMERA skrev:Sov på saken. Kom tillbaka om det inte klarnar.
PATENTERAMERA skrev:Nej. Det gäller alltid att
rgr = .
Om r <= R.
Om r > R
I första fallet då r<=R. Varför är integrationsgränsen 0 till r och ej 0 till R om r är integrationsvariabel? Man kan ju bara ersätta R^2 med r^2 då r=R i det intervallet och sen får man som du skrev.
I andra fallet då r>R så delar du upp integralen i två delar. Varför gör du det? Varför är 0 till r ekvivalent med 0 till R+R till r vad gäller gränserna? Då r>R så är det ju så att vi har R<r<inf egentligen. Det borde väl bli R till r och sen r till inf?

Är detta från facit?
Som du säkert kommer ihåg så finns det en räkneregel för integraler.
PATENTERAMERA skrev:Är detta från facit?
Nej AI. Det är väl sant?
PATENTERAMERA skrev:Som du säkert kommer ihåg så finns det en räkneregel för integraler.
Jo det vet jag. Om a=R och c=inf så blir b=r och sen r till inf
Säg att du har ekvationen
f’(x) = h(x)
Då gäller formellt
, och med utnyttjande av integralkalkylens fundamentalsats
.
Vår ekvation ser ut som
f’(r) = , där f(r) = rgr(r).
Vi har då
Är du med så långt?


