beräkna Greens formel (Matematik/Universitet)

Ditt variabelbyte till polära koordinater begriper jag inte. Vad har hänt med $r$ ? Vad har hänt med Jacobideterminanten?

AlvinB skrev:
Ditt variabelbyte till polära koordinater begriper jag inte. Vad har hänt med $r$ ? Vad har hänt med Jacobideterminanten?

jag följe den här & här ser jag inge jacobterminant.

men håller med ska ju vara

$x= r cos(t)$ osv..

Jag menar att för att få byta från kartesiska till polära koordinater krävs att man använder sig av Jacobideterminanten. I fallet med polära koordinater blir determinanten lika med $r$ .

AlvinB skrev:
Jag menar att för att få byta från kartesiska till polära koordinater krävs att man använder sig av Jacobideterminanten. I fallet med polära koordinater blir determinanten lika med $r$ .

men om man inte byter då? hur skulle det då se ut?

Då får du ju en vanlig dubbelintegral över cirkeln. Du kan googla det om du vill, det är faktiskt ett mycket använt exempel för att visa hur mycket smidigare det är att använda polära koordinater. Du får lösa ut x eller y ur ekvationen för cirkeln.

Moffen skrev:
Då får du ju en vanlig dubbelintegral över cirkeln. Du kan googla det om du vill, det är faktiskt ett mycket använt exempel för att visa hur mycket smidigare det är att använda polära koordinater. Du får lösa ut x eller y ur ekvationen för cirkeln.

Ahh säkerligen, blev bara så osäker när det efterfrågades cirkeln.

Men då anvnder jag:

a) $\int_0^1 \int_0^(\infty) dxdy$

b) $\int_0^1 \int_0^x dxdy$

stämmer det?

Bump?

Hej heymel,

Den här uppgiften går att lösa med Greens formel, men fältet är singulärt i origo och integralen är enklare att lösa med en direkt tillämpning av linjeintegralen. Står det i uppgiften att du måste använda Greens formel?

Du verkar ha deriverat fel, det gäller att

$\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}=\frac{3y^2-x^2}{(x^2+3y^2)^2}$

Villkoret

$\boxed{\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}}$

Betyder något speciellt, vad?

Hej!

Uppgift a. Kurvan $\gamma$ parameteriseras.

$\displaystyle\gamma = \{(x,y) : x(t) = \cos t \text{ och } y(t) = \sin t \ , 0 \leq t \leq \pi.\}$

Då blir

$\displaystyle\frac{-y}{x^2+3y^2}dx = -\frac{\sin t}{\cos^2 t + 3\sin^2 t} (-\sin t) dt = \frac{\sin^2 t}{\cos^2 t + 3\sin^2 t}\,dt$

och

$\displaystyle\frac{x}{x^2+3y^2}dy = \frac{\cos t}{\cos^2 t + 3\sin^2 t} (\cos t) dt = \frac{\cos^2 t}{\cos^2 t + 3\sin^2 t}\,dt$

så att kurvintegralen kan skrivas

$\displaystyle\int_{t=0}^{\pi} \frac{1}{\cos^2 t + 3\sin^2 t}\,dt = \displaystyle\int_{t=0}^{\pi} \frac{1}{1+ 2\sin^2 t}\,dt = \ldots = \frac{\pi}{\sqrt{3}}.$

Guggle skrev:
Hej heymel,

$\boxed{\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}}$
Betyder något speciellt, vad?

att vi måste paramatisera? för om vi får dom lika varann kan bero på att dom inte är kontinuerlig i punkten (0,0) ?

Albiki skrev:
Hej!
Uppgift a. Kurvan $\gamma$ parameteriseras.
$\displaystyle\gamma = \{(x,y) : x(t) = \cos t \text{ och } y(t) = \sin t \ , 0 \leq t \leq \pi.\}$
Då blir
$\displaystyle\frac{-y}{x^2+3y^2}dx = -\frac{\sin t}{\cos^2 t + 3\sin^2 t} (-\sin t) dt = \frac{\sin^2 t}{\cos^2 t + 3\sin^2 t}\,dt$

om $$x(t) = cos t

hur fick du då bråktalet multiplicerat med den extra x:et.(eller y:et). ? asså i täljaren (parentesen)

heymel skrev:
Albiki skrev:
Hej!
Uppgift a. Kurvan $\gamma$ parameteriseras.
$\displaystyle\gamma = \{(x,y) : x(t) = \cos t \text{ och } y(t) = \sin t \ , 0 \leq t \leq \pi.\}$
Då blir
$\displaystyle\frac{-y}{x^2+3y^2}dx = -\frac{\sin t}{\cos^2 t + 3\sin^2 t} (-\sin t) dt = \frac{\sin^2 t}{\cos^2 t + 3\sin^2 t}\,dt$
om $$x(t) = cos t

hur fick du då bråktalet multiplicerat med den extra x:et.(eller y:et). ? asså i täljaren (parentesen)

Jag förstår inte vad du skriver. Vilket bråktal? vilket extra x?

heymel skrev:
Guggle skrev:
Hej heymel,
$\boxed{\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}}$
Betyder något speciellt, vad?
att vi måste paramatisera? för om vi får dom lika varann kan bero på att dom inte är kontinuerlig i punkten (0,0) ?

Ja, vi har problem med punkten (0,0).

Att de blir lika innebär att integralen över ytan i Greens formel blir noll. Dessutom är linjeintegralen utmed x-axeln 0 (eftersom y=0 där och därför F=0) vilket gör det frestande att försöka använda Greens formel. Problemet är att fältet är singulärt i origo och om vi tar med den punkten i vårt integrationsområde är förutsättningarna för att få använda Greens formel inte uppfyllda.

För att få använda Greens formel måste vi därför gå runt den farliga punkten i origo (det röda krysset) så att den inte hamnar inom integrationsområdet. Ett exempel på en sådan integrationsväg är följande:

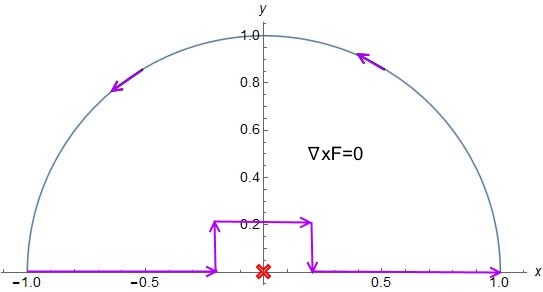
För att slippa få tre (egentligen 5) extra integraler kan man istället gå runt punkten med en halvcirkel, men då är det bättre att beräkna linjeintegralen direkt utan att krångla med Greens formel, som Albiki redan visat för uppgift a).

Det var därför jag undrade om det står i uppgiften att du måste använda Greens formel. Det finns också ett annat knep du kan använda som bygger på potentialteori runt singulära punkter då fältet i övrigt är rotationsfritt, men det brukar inte ingå i den grundläggande vektoranalysen (du kan alltså inte bara beräkna skillnaden mellan fältets "potential" i de två punkterna).

Albiki skrev:
heymel skrev:
Albiki skrev:
Hej!
Uppgift a. Kurvan $\gamma$ parameteriseras.
$\displaystyle\gamma = \{(x,y) : x(t) = \cos t \text{ och } y(t) = \sin t \ , 0 \leq t \leq \pi.\}$
Då blir
$\displaystyle\frac{-y}{x^2+3y^2}dx = -\frac{\sin t}{\cos^2 t + 3\sin^2 t} (-\sin t) dt = \frac{\sin^2 t}{\cos^2 t + 3\sin^2 t}\,dt$
om $$x(t) = cos t

hur fick du då bråktalet multiplicerat med den extra x:et.(eller y:et). ? asså i täljaren (parentesen)
Jag förstår inte vad du skriver. Vilket bråktal? vilket extra x?

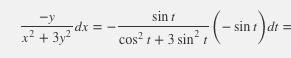
det står ju $-y$ inte $y^2$ så fattar inte varför en extra $-sin(t)$ multipliceras

Guggle skrev:
heymel skrev:
Guggle skrev:
Hej heymel,
$\boxed{\frac{\partial Q}{\partial x}=\frac{\partial P}{\partial y}}$
Betyder något speciellt, vad?
att vi måste paramatisera? för om vi får dom lika varann kan bero på att dom inte är kontinuerlig i punkten (0,0) ?
Ja, vi har problem med punkten (0,0).
Att de blir lika innebär att integralen över ytan i Greens formel blir noll. Dessutom är linjeintegralen utmed x-axeln 0 (eftersom y=0 där och därför F=0) vilket gör det frestande att försöka använda Greens formel. Problemet är att fältet är singulärt i origo och om vi tar med den punkten i vårt integrationsområde är förutsättningarna för att få använda Greens formel inte uppfyllda.
För att få använda Greens formel måste vi därför gå runt den farliga punkten i origo (det röda krysset) så att den inte hamnar inom integrationsområdet. Ett exempel på en sådan integrationsväg är följande:
För att slippa få tre (egentligen 5) extra integraler kan man istället gå runt punkten med en halvcirkel, men då är det bättre att beräkna linjeintegralen direkt utan att krångla med Greens formel, som Albiki redan visat för uppgift a).
Det var därför jag undrade om det står i uppgiften att du måste använda Greens formel. Det finns också ett annat knep du kan använda som bygger på potentialteori runt singulära punkter då fältet i övrigt är rotationsfritt, men det brukar inte ingå i den grundläggande vektoranalysen (du kan alltså inte bara beräkna skillnaden mellan fältets "potential" i de två punkterna).

Aaa.. Intressat :) Nä har inte hört talas som potentialteori runt singälar punkter. ;s