Beräkna hastighet (Fysik/Fysik 1)

Såhär tänker jag:

Äpple skrev:
Albin står på ett berg släpper en liten metallkula rakt ner och mäter falltiden. Faller varar i 3s. Vi antar att kulan faller fritt.

a) Beräkna höjden på berget.

s= (3•3•-9,82)/2=-44,19( alltså fallit 44.19 m)

Formeln lyder s = s₀+v₀t+at²/2.

Om du säger att markytan är nollnivå och positiv riktning är uppåt så släpps kulan från en viss höjd s₀ och faller ner mot höjden 0.

Då gäller det att

s = 0 m, dvs marknivån

s₀ = höjden på berget i meter

v₀ = 0 m/s, dvs utgångshastigheten

a $\approx$ -9,82 m/s², dvs tyngdaccelerationen

t = 3 s, dvs tidsåtgången

Du får då ekkvationen

0 $\approx$ s₀+0•3-9,82•3²/2

s₀ $\approx$ 4,5•9,82 $\approx$ 44 meter

Är mina berökningar rätta? Läraren skriver inte med negativ tyngd acceleration

Se ovan. Du väljer själv vilken riktning som är positiv.

Om du väljer att uppåt är positiv så ska a vara lika med -g.

Om du väljer att neråt är positiv riktning så ska a vara lika med g, men du måste då även se till att s och s₀ anpassas efter denna riktning.

Yngve skrev:
Äpple skrev:
Albin står på ett berg släpper en liten metallkula rakt ner och mäter falltiden. Faller varar i 3s. Vi antar att kulan faller fritt.

a) Beräkna höjden på berget.

s= (3•3•-9,82)/2=-44,19( alltså fallit 44.19 m)

Formeln lyder s = s₀+v₀t+at²/2.

Om du säger att markytan är nollnivå och positiv riktning är uppåt så gäller det att

s = 0 m, dvs marknivån

s₀ = höjden på berget i meter

v₀ = 0 m/s, dvs utgångshastigheten

a = -9,82 m/s², dvs tyngdaccelerationen

t = 3 s, dvs tidsåtgången

Du får då ekkvationen

0 = s₀+0•3-9,82•3²/2

s₀= 4,5•9,82 $\approx$ 44 meter

Är mina berökningar rätta? Läraren skriver inte med negativ tyngd acceleration

Se ovan. Du väljer själv vilken riktning som är positiv.

Om du väljer att uppåt är positiv så ska a vara lila med -g.

Om du väljer att neråt är positiv riktning så ska a vara lika med g, men du måste då även se till att s och s₀ anpassas efter denna riktning.

Men v₀är väl lika med 10m/s eftersom han kastar kulan med den utgångshastigheten.

maestro! skrev:

Men v₀är väl lika med 10m/s eftersom han kastar kulan med den utgångshastigheten.

Jag räknade på a-uppgiften. Där är utgångshastigheten lika med 0 m/s.

Yngve skrev:
maestro! skrev:

Men v₀är väl lika med 10m/s eftersom han kastar kulan med den utgångshastigheten.

Jag räknade på a-uppgiften. Där är utgångshastigheten lika med 0 m/s.

Jag insåg nu att jag trodde att båda a och b uppgiften hade samma v_0, ber om ursäkt för det därför väldigt konstiga svaret från min del i a uppgiften. Det blir alltså s=0,5*9,82*3²=44,19m/s

ok, men varför blir b fel? Jag räknade ju rätt på A?

Äpple skrev:
ok, men varför blir b fel? Jag räknade ju rätt på A?

Fråga B är felformulerad eller så saknas det information om i vilken riktning kulan kastades.

han kastar kulan ner, blir det rätt då med min beräkning?

Nej det blir inte rätt. Du använder formeln v = v₀+at, vilket är rätt, men dels så tar det mindre än 3 sekunder för kulan att nå marken om Albin kastar den rakt neråt, dels så har du fel tecken på ursprungshastigheten om du anser att positiv riktning är uppåt.

========= Så här kan du göra =======

Om Albin kastar kulan rakt neråt så är rörelsen endast i en dimension. Då gäller samma formel som i svar #3, dvs s = s₀+v₀t+at²/2.

Med samma nollnivå och riktning som tidigare gäller

s = 0 m, dvs marknivå.

s₀ $\approx$ 44 m, dvs bergets höjd.

v₀ = -10 m/s, utgångshastigheten.

a $\approx$ -9,82 m/s², tyngdaccelerationen

t är okänd eftersom det inte längre tar 3 sekunder för kulan att nå marken.

Du får då ekvationen 0 $\approx$ 44-10t-9,82t²/2. Lös ut t ur denna ekvation så kan du sedan använda v = v₀+at för att beräkna sluthastigheten v.

Pröva gärna sedan vad som händer om Albin kastar kulan rakt uppåt istället.

========

Ett annat och enklare sätt är att använda ett energiresonemang. Du kan då utnyttja att den vertikala hastighetsökningen kommer från att kulan förlorar en del av sin lägesenergi.

Mängden lägesenergi den förlorar är cirka 44mg, enligt E_p = mgh.

Denna energimängd har gått åt till att öka hastigheten med mv₁²/2, enligt E_k = mv²/2.

Eftersom 44gh = mv₁2/2 så får du v₁ = - $\sqrt{2\cdot44\cdot g}$ .

Addera nu denna hastighetsökning med ursprungshastigheten -10 m/s.

Yngve skrev:
Nej det blir inte rätt. Du använder formeln v = v₀+at, vilket är rätt, men dels så tar det mindre än 3 sekunder för kulan att nå marken om Albin kastar den rakt neråt, dels så har du fel tecken på ursprungshastigheten om du anser att positiv riktning är uppåt.

========= Så här kan du göra =======

Om Albin kastar kulan rakt neråt så är rörelsen endast i en dimension. Då gäller samma formel som i svar #3, dvs s = s₀+v₀t+at²/2.

Med samma nollnivå och riktning som tidigare gäller

s = 0 m, dvs marknivå.

s₀ $\approx$ 44 m, dvs bergets höjd.

v₀ = -10 m/s, utgångshastigheten.

a $\approx$ -9,82 m/s², tyngdaccelerationen

t är okänd eftersom det inte längre tar 3 sekunder för kulan att nå marken.

Du får då ekvationen 0 $\approx$ 44-10t-9,82t²/2. Lös ut t ur denna ekvation så kan du sedan använda v = v₀+at för att beräkna sluthastigheten v.

Pröva gärna sedan vad som händer om Albin kastar kulan rakt uppåt istället.

========

Ett annat och enklare sätt är att använda ett energiresonemang. Du kan då utnyttja att den vertikala hastighetsökningen kommer från att kulan förlorar en del av sin lägesenergi.

Mängden lägesenergi den förlorar är cirka 44mg, enligt E_p = mgh.

Denna energimängd har gått åt till att öka hastigheten med mv₁²/2, enligt E_k = mv²/2.

Eftersom 44gh = mv₁2/2 så får du v₁ = - $\sqrt{2\cdot44\cdot g}$ .

Addera nu denna hastighetsökning med ursprungshastigheten -10 m/s.

Ska svaret vara -20m/s?

Äpple skrev:

Ska svaret vara -20m/s?

Nej.

Visa dina uträkningar så kan vi hjälpa dig att hitta felet.

Yngve skrev:
Äpple skrev:

Ska svaret vara -20m/s?

Nej.

Visa dina uträkningar så kan vi hjälpa dig att hitta felet.

Jag infogade min beräkning via redigering så att du vet.

De två sakerna inringade i blått stämer inte.

Det gäller inte att t = -v₀/a

Den andra förstår jag inte alls.

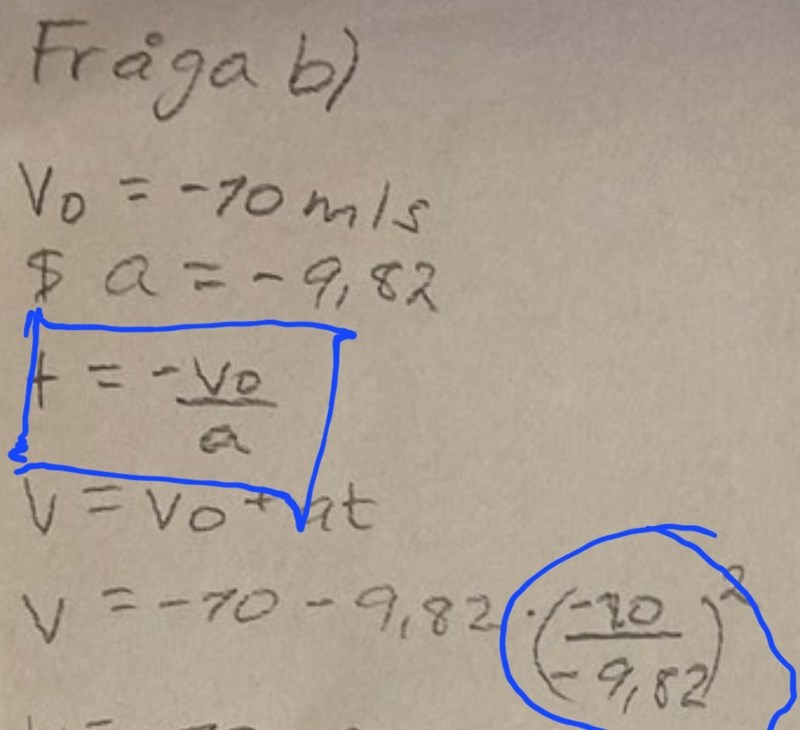
Räkna istället på något av de sött jag visade dig.

Yngve skrev:
Äpple skrev:

Ska svaret vara -20m/s?

Nej.

Visa dina uträkningar så kan vi hjälpa dig att hitta felet.

Jo det går. t=(v-v0)/a. Vi har ingen hastighet så därför blir det -starthastighet

de sätt som du visade mig känner jag inte till och vill enbart använda mig av de formler som lärare gett mig:)

Äpple skrev:

Jo det går. t=(v-v0)/a. Vi har ingen hastighet så därför blir det -starthastighet

Jag ser från din uträkning att v₀ = -10 m/s.

Men vad är v och vad menar du med att vi inte har någon starthastighet?

de sätt som du visade mig känner jag inte till och vill enbart använda mig av de formler som lärare gett mig:)

OK, då försöker vi använda endast dem. Vilka formler har din lärare gett dig?

Jag löste med din formel. En fråga, kommer S i din formel alltid vara 0?

På fråga b) löste jag ut t vilket gav mig 2.15 s

När jag satte in tiden t i formeln för hastighet fick jag v till=-31.1?

Alltså att bollen är på väg ner med hastigheten 31,1 m/s?

Om Albin kastar kulan rakt uppåt:

Blir inte tiden 2.15 och hastigheten samma? Jag är helt borta. Jag behöver hjälp där.

Är det rätt?

Äpple skrev:
Jag löste med din formel. En fråga, kommer S i din formel alltid vara 0?

Nej, inte alltid. Det beror på sammanhanget.

På fråga b) löste jag ut t vilket gav mig 2.15 s

När jag satte in tiden t i formeln för hastighet fick jag v till=-31.1?

Alltså att bollen är på väg ner med hastigheten 31,1 m/s?

Ja, det ser bra ut. Men avrunda till färre siffror i svaret.

Om Albin kastar kulan rakt uppåt:

Blir inte tiden 2.15 och hastigheten samma? Jag är helt borta. Jag behöver hjälp där.

Du kan tänka på samma sätt, men v₀ är då +10 m/s, inte -10 m/s.

Hej! Men läraren sa till mig att man ska räkna med tiden 3 s k fråga b och att den inte är okänd????

Jag förstår inte riktigt vad du menar.

Så här är det:

När Albin släpper kulan rakt ner tar det 3 sekunder innan kulan når marken, så där är tiden inte okänd.

När Albin kastar iväg kulan så beror tiden på i vilken riktning Albin kastar.

Om Albin kastar kulan rakt neråt så tar det mindre tid än 3 sekunder.
Om Albin kastar kulan rakt uppåt så tar det längre tid än 3 sekunder.
Om Albin kastar kulan rakt fram tar det 3 sekunder.

Äpple skrev:
Hej! Men läraren sa till mig att man ska räkna med tiden 3 s k fråga b och att den inte är okänd????

I så fall räknar din lärare med att Albin kastar kulan rakt ut. Det är fullt möjligt att det är så det är menat,men det framgår inte av uppgiftens formulering. Om man kastar en kula, så har kulan både hfart och riktning. Om man bara anger farten, kan man få olika svar beroende på vilken riktning man antar att kulan har.

Läs mitt svar #8 igen.

Yngve skrev:
Läs mitt svar #8 igen.

Min lärare sa att frågan var rätt och att hans svar var rätt

Äpple skrev:
Yngve skrev:
Läs mitt svar #8 igen.

Min lärare sa att frågan var rätt och att hans svar var rätt

Fråga din lärare hur du skall veta i vilken riktning Albin kastade kulan.

Men enligt läraren betyder det inte att stenen fallit 30m? Stenen faller med 9.82m/s^2•3=30 m när höjden är 44

Smaragdalena skrev:
Äpple skrev:
Yngve skrev:
Läs mitt svar #8 igen.

Min lärare sa att frågan var rätt och att hans svar var rätt

Fråga din lärare hur du skall veta i vilken riktning Albin kastade kulan.

Albin kastar kulan ner

Äpple skrev:
Men enligt läraren betyder det inte att stenen fallit 30m? Stenen faller med 9.82m/s^2•3=30 m när höjden är 44

Vad menar du med detta? (Nu räknar jag med g = 10 m/s² för enkelhets skull.)

Om Albin kastar kulan neråt så är hastigheten 10 m/s när t = 0 och 20 m/s när t = 1, så medelhastigheten den första sekunden är 15 m/s och kulan har fallit 15 m under den första sekunden.

Hastigheten är 20 m/s när t = 1 och 30 m/s när t = 2, så medelhastigheten den andra sekunden är 25 m/s och kulan har fallit 25 m under den första sekunden, alltså 40 m de två första sekunderna.

Om höjden är 44 m, så har stenen har slagit i marken innan det har gått 3 sekunder.

Jag förstår mindre och mindre.

Jag tror att vi behöver veta exakt hur uppgiften lyder (helst med bild), exakt vad det står i facit (helst med bild) och exakt hur din lärares uträkning ser ut (helst med bild).

Det här är den exakta uppgifter med det exakta svaret som han skrev

Bilden syns inte.

nu?

Nej.

Din lärare menar $\,^*$ på b) uppgiften att det fortfarande tar 3 sekunder för stenen att nå marken.

Det betyder att vi har ett nytt berg som är högre än det berg man befann sig på under fråga a).

Använd formeln

$v=v_0+at$

$v=10\mathrm{m/s}+(9.82\mathrm{m/s^2})\cdot (3\mathrm{s})\approx 40\mathrm{m/s}$

Edit: $\,^*$ Gissar jag att läraren menar kanske jag ska tillägga

jag förstår inte vad som menas med ett nytt berg

Om kulan fortfarande skall falla i 3 sekunder, fastän man kastar den neråt, så måste man starta högre upp än 44 m. Det är det som D4NIEL menar med "ett annat berg".

Men va? Läraren sa att det är exakt samma berg med att tiden för det att falla tar 3 s även om man har en starthastighet men min fråga är varförrr

Äpple skrev:
Men va? Läraren sa att det är exakt samma berg med att tiden för det att falla tar 3 s även om man har en starthastighet men min fråga är varförrr

Om det tar lika lång tid för kulan att nå marken oavsett om den släpps från vila eller om den kastas ut med en viss starthastighet så beror det på att kastet är helt horisontellt, se även svar #23 och svar #24.

Att det då tar lika lång tid beror på att den vertikala starthastigheten i så fall är densamma i de båda fallen, nämligen 0 m/s.

Men vi bara fortsätter att gissa hur uppgiften lyder, vilket inte känns speciellt bra. Försök gärna att ladda upp bilderna igen.

Då har din lärare räknat fel.

Såg du bilden? Nej han säger att han räknar rätt och provet är på fredag… jag kan ju inte säga till honom att han räknar fel då han står på sitt aja

Alla gör fel ibland. Elever gör fel, vi på Pluggaluten gör fel, lärare gör fel.

Det här var ett exempel på det sistnämnda.

Men det var bra att räta ut frågetecknen.

==============

Förklaring till varför din lärare inte hade negativt värde på acceleration och starthastighet:

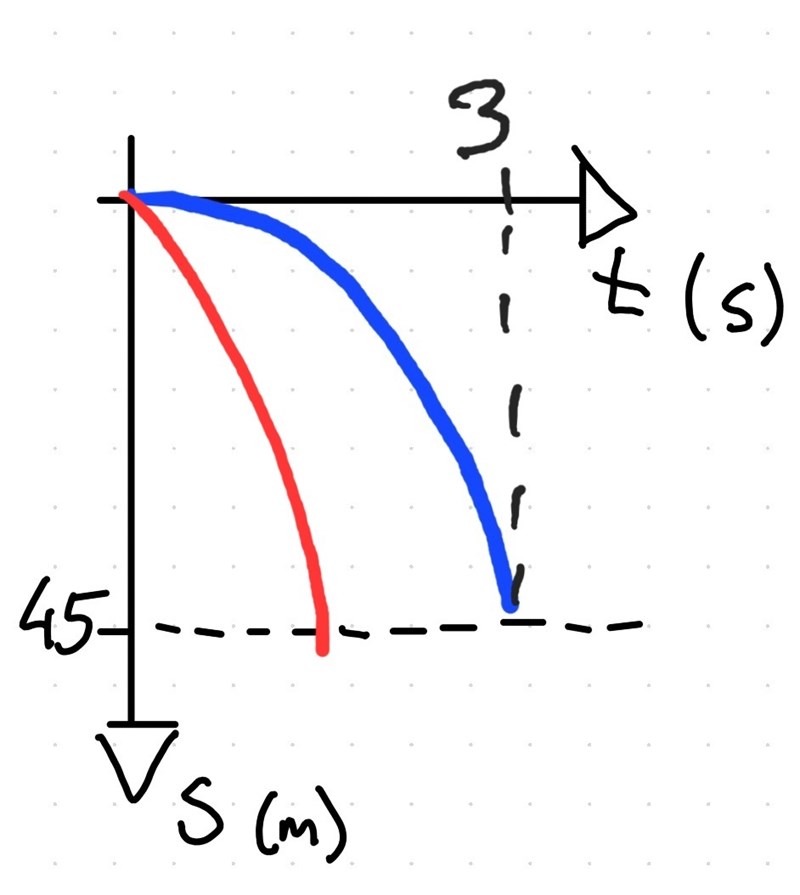
Läraren lade nollnivån vid utkastplatsen och valde neråt som positiv riktning, se skiss som visar kulans position s vid olika tidpunkter t.

Blå parabel = kulan släpps från vila, röd parabel = kulan kastas neråt. Det är tydligt att den röda parabeln når nivån 45 meter på mindre än 3 sekunder.

Skissen illustrerar även att starthastigheten är lika med parabelns lutning vid t = 0. Den blå parabeln har lutning 0 där, vilket motsvarar starthastigheten 0 m/s. Den röda parabeln har lutning 10 där (tänk på att positiv riktning är neråt!), vilket motsvarar starthastigheten 10 m/s.

Äpple skrev:
Såg du bilden? Nej han säger att han räknar rätt och provet är på fredag… jag kan ju inte säga till honom att han räknar fel då han står på sitt aja

Ja, nu syns bilden. Läraren räknar rätt på a-uppgiften och fel på b-uppgiften.

Jag tycker att det är viktigt att din lärare får veta att uträkningen är fel. Om du inte vill säga det direkt till honom kan du skicka en länk till denna tråd, men tänk då på att han i så fall får reda på vem Äpple är och att han kan se alla dina andra trådar här.

==============

Om du vill skicka länken:

Tryck och håll (eller högerklicka) på #1 i trådstarten (se bild) och välj "kopiera länk".

Den kan du skicka till läraren.