Beräkna integralen (Matematik/Universitet/Övrigt)

Använd Gauss sats för tensorer.

$\oint_{S} A_{i_{1} \dots i_{n}} d S_{j} = \int_{V} \partial_{j} A_{i_{1} \dots i_{n}} d V$ .

PATENTERAMERA skrev:
Använd Gauss sats för tensorer.

$\oint_{S} A_{i_{1} \dots i_{n}} d S_{j} = \int_{V} \partial_{j} A_{i_{1} \dots i_{n}} d V$ .

Varför gaus sats? Varför gaus sats för tensorer? Hur är detta tensorer??

Tensorer är ju en generalisering som innefattar vektorer som ett specialfall.

Om du inte vill använda tensorer så är ett tips att använda bac-cab-regeln.

dS x (a x r) = a(r•dS) - r(a•dS).

Första termen.

$\oint_{S} \vec{a} (\vec{r} \cdot d \vec{S}) = \vec{a} \oint_{S} \vec{r} \cdot d \vec{S} = (G a u s s) = \vec{a} \int_{V} \nabla \cdot \vec{r} d V = 3 \vec{a} V$ .

Andra termen: gör själv.

PATENTERAMERA skrev:
Om du inte vill använda tensorer så är ett tips att använda bac-cab-regeln.

dS x (a x r) = a(r•dS) - r(a•dS).

Första termen.

$\oint_{S} \vec{a} (\vec{r} \cdot d \vec{S}) = \vec{a} \oint_{S} \vec{r} \cdot d \vec{S} = (G a u s s) = \vec{a} \int_{V} \nabla \cdot \vec{r} d V = 3 \vec{a} V$ .

Andra termen: gör själv.

Kan man använda index här? Den där bac-cab regeln känner jag igen från mekaniken. Jag förstår dock inte hur det blir gaus samt a(nablar)=3aV?

Gauss säger att

$\oint_{S} \vec{A} \cdot d \vec{S} = \int_{V} \nabla \cdot \vec{A} d V$ .

Här är $\vec{A} = \vec{r}$ . $\nabla \cdot \vec{r} = 3$ .

Ja, man kan använda index, som jag indikerade i #2.

PATENTERAMERA skrev:
Gauss säger att

$\oint_{S} \vec{A} \cdot d \vec{S} = \int_{V} \nabla \cdot \vec{A} d V$ .

Här är $\vec{A} = \vec{r}$ . $\nabla \cdot \vec{r} = 3$ .

Ja, man kan använda index, som jag indikerade i #2.

Ok om jag använder index så har jag alltså DSjeijk(eklmalrm)?

Ja.

PATENTERAMERA skrev:
Ja.

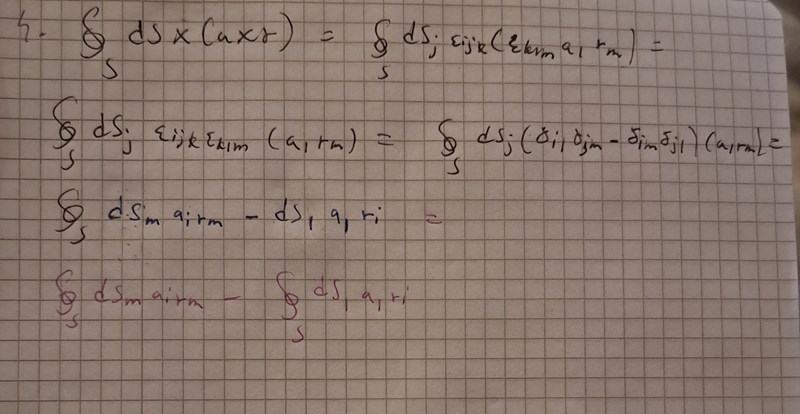
Såhär blev det. Vad blir nästa steg?

Använd Gauss från #1.

Tex

$\oint_{S} d S_{m} a_{i} r_{m} = \int_{V} \partial_{m} (a_{i} r_{m}) d V$ .

PATENTERAMERA skrev:
Använd Gauss från #1.

Tex

$\oint_{S} d S_{m} a_{i} r_{m} = \int_{V} \partial_{m} (a_{i} r_{m}) d V$ .

Hur vet jag att VL motsvarar HL som är gaus sats?

Det är bara en tillämpning av Gauss sats från #2 på denna speciella situation.

PATENTERAMERA skrev:
Det är bara en tillämpning av Gauss sats från #2 på denna speciella situation.

Jag tror tyvärr inte att jag hänger med. Jag ser inte hur just den termen på HL motsvarar gaus sats i #11.

Gauss säger att

$\oint_{S} (t e n s o r) d S_{m} = \int_{V} \partial_{m} (t e n s o r) d V$

I vårt fall så är tensor = a_ir_m.

PATENTERAMERA skrev:
Gauss säger att

$\oint_{S} (t e n s o r) d S_{m} = \int_{V} \partial_{m} (t e n s o r) d V$

I vårt fall så är tensor = a_ir_m.

OK så jag antar att det är en definition på gaus sats då? Hur vet man förresten att det är en tensor ? I vanliga fall är det väl (vektorfält eller skalärfält)*Ds_m?

Såhär fick jag nu.

Bra. Fortsätt.

Tillägg: 9 dec 2025 13:45

Tänk på att a är konstant.

PATENTERAMERA skrev:
Bra. Fortsätt.

Tillägg: 9 dec 2025 13:45

Tänk på att a är konstant.

a är en konstant vektor menar du?

Ja.

PATENTERAMERA skrev:
Ja.

Kan du svara på #16?

Den generella formeln funkar för alla tensorer, skalärer och vektorer är bara specialfall.

Tillägg: 9 dec 2025 13:49

Skalär - nollte ordningens tensor.

Vektor - första ordningens tensor.

Tillägg: 9 dec 2025 14:01

När du använder indexräkning kan du alltid säga att det är frågan om tensorer.

PATENTERAMERA skrev:
Den generella formeln funkar för alla tensorer, skalärer och vektorer är bara specialfall.

Tillägg: 9 dec 2025 13:49

Skalär - nollte ordningens tensor.

Vektor - första ordningens tensor.

Tillägg: 9 dec 2025 14:01

När du använder indexräkning kan du alltid säga att det är frågan om tensorer.

Aa ok. Såhär fick jag

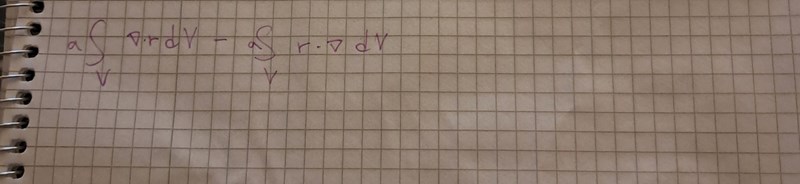
Visa hur du gör med index.

PATENTERAMERA skrev:
Visa hur du gör med index.

Jag har inte gjort något mer än #17. Du sa att jag ska fortsätta så jag omvandlade det där till vektornotation.

Var du kanske ute efter ett sånt svar?

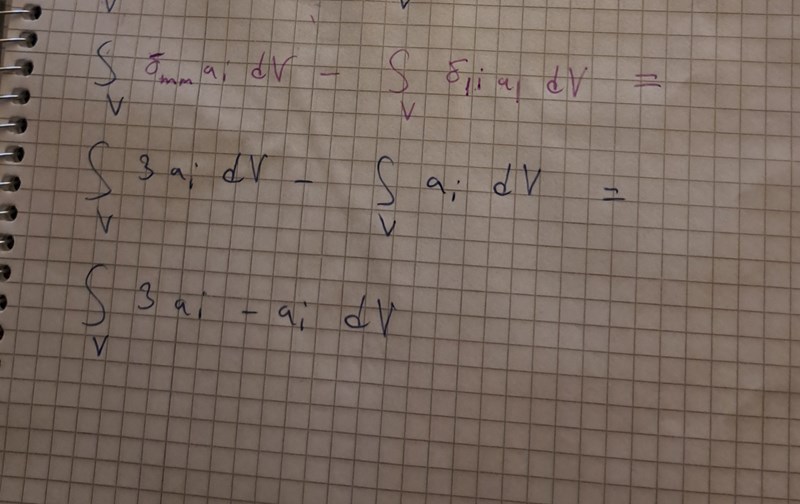
Ja, nu ser det rätt ut. Sedan kan du bryta ut a_i utanför integralen. Så svaret blir

2a_iV (eller 2aV på vektorform). V är volymen.

PATENTERAMERA skrev:
Ja, nu ser det rätt ut. Sedan kan du bryta ut a_i utanför integralen. Så svaret blir

2a_iV (eller 2aV på vektorform). V är volymen.

Jag fick såhär. Det ska vara 2a dV. Men det står beräkna integralen. Hur gör man då?

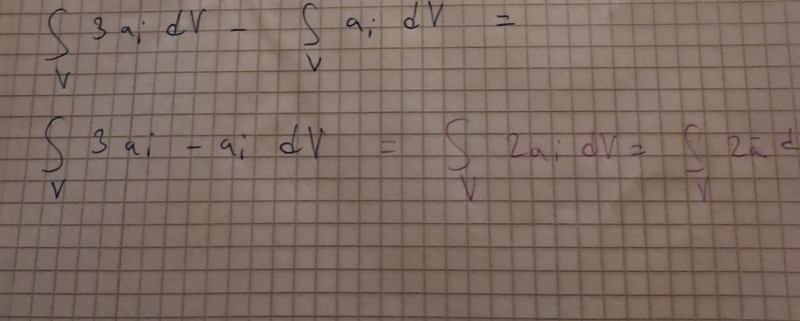
$\int_{V} d V$ = Volymen av V som vi enklast också kallar V.

PATENTERAMERA skrev:
$\int_{V} d V$ = Volymen av V som vi enklast också kallar V.

Varför blir det detta lika med V?

Det är väl närmast hur volymen av ett område definieras.

PATENTERAMERA skrev:
Det är väl närmast hur volymen av ett område definieras.

Så det är detta som gäller ?

Ja.