Beräkna integralen som ges av en olikhet.

Ellinor skrev:

Hej! Jag ska lösa följande uppgift och skulle behöva tips för att komma vidare: 

Eftersom integralen saknar primitiv funktion om man låter x eller y vara konstanta, och eftersom området man integrerar får lite komplicerade gränser, tänkte jag försöka med variabelbyte men jag har experimenterat länge med olika byten utan att komma riktigt någon vart.

Jag har till exempel testat att sätta (2x+2y)^2 = u men då vet jag inte vad jag ska sätta v till. Jag har tänkt v = 0 men det blir konstigt, då kan jag inte beräkna någon funktionaldeterminant. Jag har också till exempel prövat med att utveckla cosinustermen med additionsformeln men då hittar jag inget bra variabelbyte. Stort tack för tips. 

Det här liknar ett problem som postades för en dag sedan, om integration av nivåkurvor. Kan du lägga upp bilder på lärobokens föreslagna metod så vi "lär oss" så skall vi nog ge korrekt hjälp i denna fråga.

Självklart! Den metoden hade jag inte tänkt på, kan den dock inte, vet bara att den existerar

Jag ska titta på exempel 18. 

Har inte tänkt färdigt på detta men bara ett hugskott:

Om u = (2x+2y)² där 2x+2y har gränserna 4 till 8 så har du

cos u där u går från 0 till pi/2 radianer.

Integrationsområdet

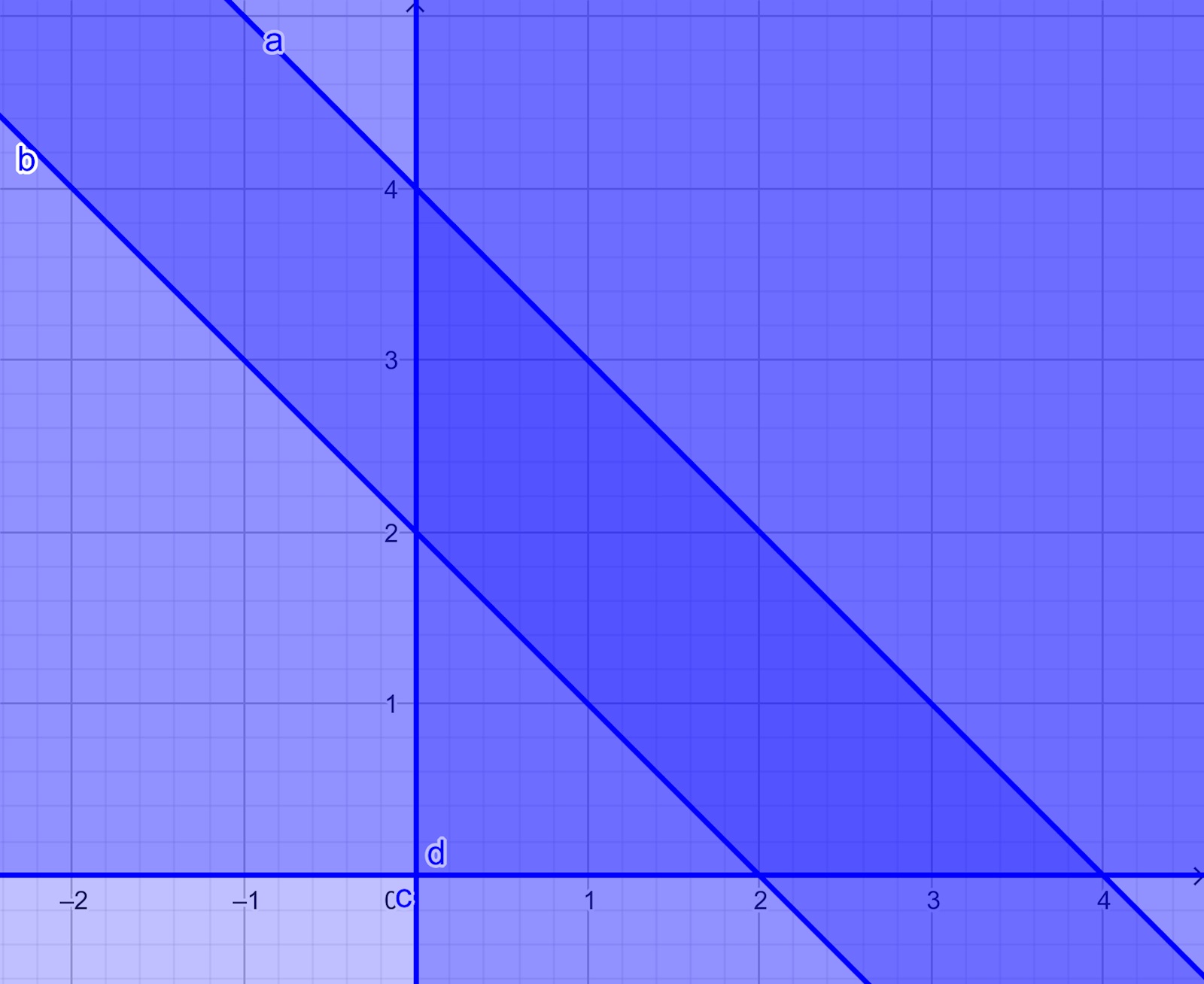
Ja, det har jag ritat upp i mitt block.

Marilyn skrev:

Har inte tänkt färdigt på detta men bara ett hugskott:

Om u = (2x+2y)² där 2x+2y har gränserna 4 till 8 så har du

cos u där u går från 0 till pi/2 radianer.

Jag förstår inte riktigt, om u = (2x+2y)^2, borde inte gränserna bli 16 och 64 då? Hur får cos u gränserna 0 till pi/2 radianer? Hur blir det då med funktionaldeterminanten d(x,y)/d(u,v) som man behöver beräkna när vi inte har något v?

Jag sitter och tittar på exemplet, men förstår inte vad området G_u ges av i mitt fall? Är det någon som vet? 

Ellinor skrev:

Jag sitter och tittar på exemplet, men förstår inte vad området G_u ges av i mitt fall? Är det någon som vet? 

Kan du lägga upp sida 240+?

Självklart!

Jag blev inte så mycket klokare av det exemplet så jag tittade istället på föreläsningsanteckningar från min skola istället:

Där hade de ett exempel som mer liknar min uppgift så försökte följa stegen till punkt och pricka (utan att egentligen förstå vad jag gör) men fick ändå fel.

Ett försök...

$$\begin{gathered} h\left(g\right)=8 \cos \left(g\right) \\ g(x,y) = {\left(2x + 2y\right)}^2 \end{gathered}$$

Vad är areafunktionen eller dess derivata?

$∆A\left(u\right) = \frac{u + u + ∆u}{2} ·\frac{∆u}{\sqrt{2}}$

$A^{\text{'}}\left(u\right) = \underset{∆u\to 0}{\lim }\frac{∆A\left(u\right)}{∆u} =\underset{∆u\to 0}{\lim }\left(\left(u + \frac{∆u}{2}\right)\frac{1}{\sqrt{2}}\right) = \frac{u}{\sqrt{2}}$

$u = x + y, 2 \le u \le 4$

$$\begin{gathered} {\int }_2^{4}8 \cos \left(4u^2\right) ·\frac{u}{\sqrt{2}} du ={\int }_2^{4}4 \cos \left(4u^2\right) ·\frac{1}{\sqrt{2}} d{u}^2 = \\ ={\int }_2^4\cos \left(4u^2\right) ·\frac{1}{\sqrt{2}} d\left(4u^2\right) =\frac{1}{\sqrt{2}}{\left[\sin \left(4u^2\right)\right]}_2^4 = \frac{\sin 64 - \sin 16}{\sqrt{2}}\approx 0.441 \end{gathered}$$

Tack så mycket för försöket!! Programmet säger dock att det inte är rätt..

Äsch... Men det kändes lite som att jag missade något.

Det var nog här:

$∆A\left(u\right) = \frac{u + u + ∆u}{2\sqrt{2}} ·\frac{∆u}{\sqrt{2}}$

Men då blir

$A^{\text{'}}\left(u\right) = \underset{∆u\to 0}{\lim }\frac{∆A\left(u\right)}{∆u} =\underset{∆u\to 0}{\lim }\left(\left(\frac{2u + ∆u}{2\sqrt{2}}\right)\frac{1}{\sqrt{2}}\right) = \frac{u}{2}$

$$\begin{gathered} {\int }_2^{4}8 \cos \left(4u^2\right) ·\frac{u}{2} du ={\int }_2^{4}4\cos \left(4u^2\right) · du = \\ ={\int }_2^{4}2\cos \left(4u^2\right) · d\left(u^2\right) =\frac{1}{2}{\left[\sin \left(4u^2\right)\right]}_2^4 = \frac{\sin 64 - \sin 16}{2} \end{gathered}$$

Ett nytt försök...

MaKe skrev:

Äsch... Men det kändes lite som att jag missade något.

Skall det inte vara A'(u)=u?

MaKe skrev:

Äsch... Men det kändes lite som att jag missade något.

Det var nog här:

$∆A\left(u\right) = \frac{u + u + ∆u}{2\sqrt{2}} ·\frac{∆u}{\sqrt{2}}$

Men då blir

$A^{\text{'}}\left(u\right) = \underset{∆u\to 0}{\lim }\frac{∆A\left(u\right)}{∆u} =\underset{∆u\to 0}{\lim }\left(\left(\frac{2u + ∆u}{2\sqrt{2}}\right)\frac{1}{\sqrt{2}}\right) = \frac{u}{2}$

$$\begin{gathered} {\int }_2^{4}8 \cos \left(4u^2\right) ·\frac{u}{2} du ={\int }_2^{4}4\cos \left(4u^2\right) · du = \\ ={\int }_2^{4}2\cos \left(4u^2\right) · d\left(u^2\right) =\frac{1}{2}{\left[\sin \left(4u^2\right)\right]}_2^4 = \frac{\sin 64 - \sin 16}{2} \end{gathered}$$

Ett nytt försök...

Programmet godkänner inte det svaret heller :(

Mitt förslag enligt bilden. 

Det var rätt, tack! Men jag förstår inte riktigt vad som händer? Hur vet man vad området D_u är? Varför blir gränserna för u så som de blir? Stort tack. 

I exemplet från föreläsningen har de det ursprungliga området (ska vara större/mindre än eller lika med men kan ej skriva det)  x>0, y> 0, 1<x+2y<2, och när de sätter u = x + 2y får de gränserna 1<x+2y<u av någon anledning? Vilket i det här fallet borde bli 4<2x+2y<u