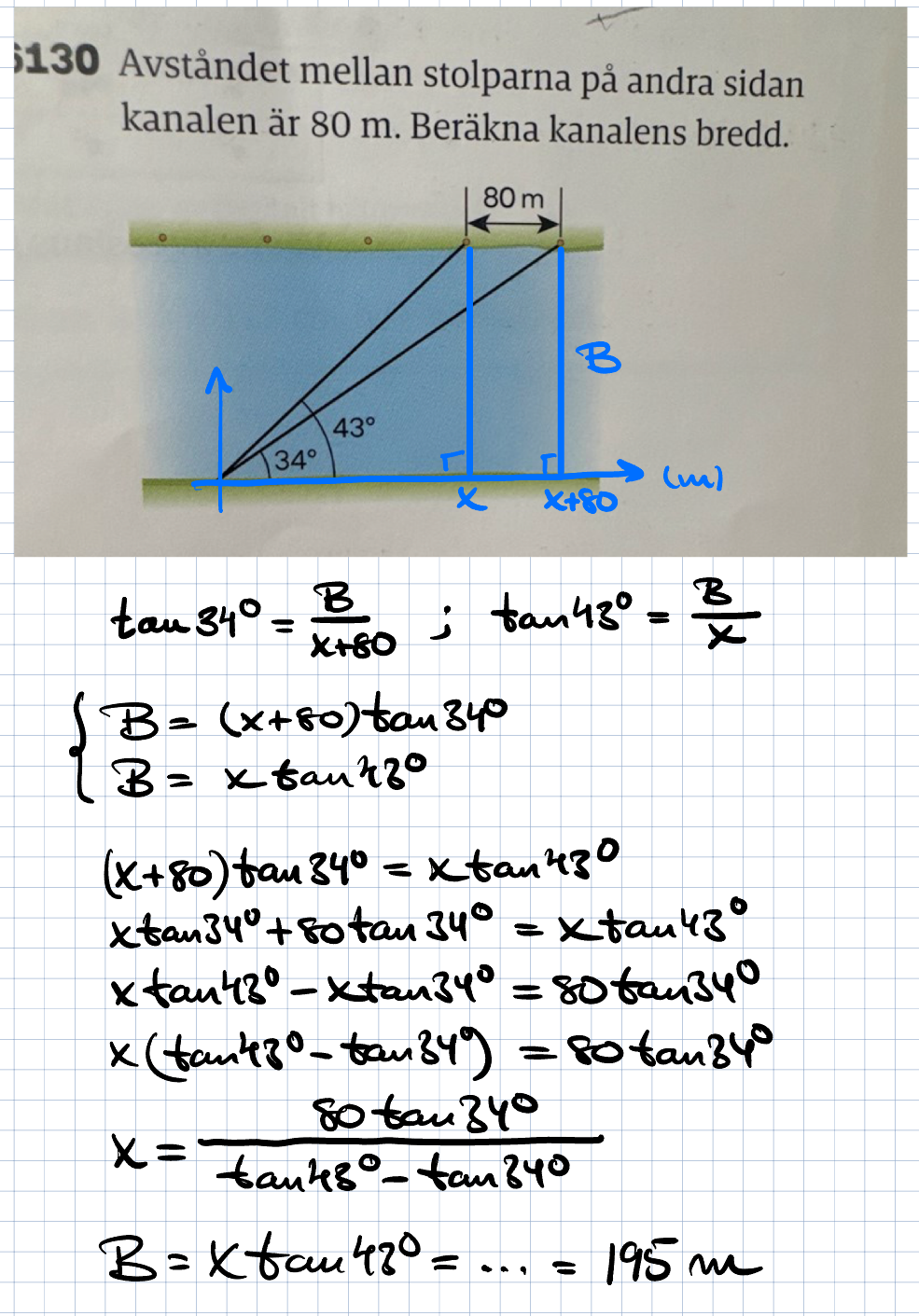
Beräkna kanalens bredd
Hej! Jag försökte lösa följande uppgift:
 Men jag kom inte fram till rätt svar, trots att jag la ner mycket tid på att förstå hur man borde gå tillväga. Jag undrar nu vad jag gjort fel. Eller om jag t.o.m. valt helt fel tillvägagångssätt.
Men jag kom inte fram till rätt svar, trots att jag la ner mycket tid på att förstå hur man borde gå tillväga. Jag undrar nu vad jag gjort fel. Eller om jag t.o.m. valt helt fel tillvägagångssätt.

Du har gjort ett enkelt räknefel, antagligen därför att du skriver för mycket.
Skriv inte ut alla siffror hela tiden, utan använd tan(43) och tan(34) fram tills du ska räkna fram a på sista raden.
Då skriver du t.ex. tan(43)/tan(34) i stället för 1.382510469
jahaa. Jo, jag tänkte på att jag kanske borta ha behållit tan(43) och tan(34) lite längre i min beräkning, men av någon anledning kändes det skönare att se siffrorna så man vet vad man ska göra liksom. Men då ska jag ändra det. Tack för din feedback!
Och då blir det lättare att hitta din lilla miss, eller hur?
inte helt säker om jag ska vara ärlig. Men jag tänker att jag från början borde dividerat båda led med tan(34)•b?
problemet då blir att man då får tan(43)/tan(34)• b/b
och b/b=1 så då försvinner ju varanen helt och då blir det ju fel….
eller så tänker jag helt fel. Kanske kommer tan(43)/tan(34) bli bur många b vi har?
man vill ju lösa ut b
Så här skulle jag göra: a/tan(34) - a/tan(43) = 80.
a(1/tan(34) - 1/tan(43)) = 80
a = 80/(1/tan(34) - 1/tan(43))
Hur kommer du fram till detta uttryck:
a/tan(34) - a/tan(43)
Edit: Nu har jag en gissning:
tan(43)=a/b
Kan det då betyda att b=a/tan(43) (stämmer detta?)
Och vi vet att det är 80 meter skillnad mellan baserna på de två trianglarna. Om man då räknar ut differensen mellan de två baserna ska man få 80.
(b+80)*tan(34) = a -> b+80 = a/tan(34)
b*tan(43) = a -> b = a/tan(43)
ahaa, då förstår jag. Ska göra ett försök att lösa den på egen hand nu :)
 känns som att jag är fel ute…
känns som att jag är fel ute…
Lag gör fortfarande något väldigt fel, jag förstår inte, för jag försökte göra allt som du gjorde, och uttrycket (x+80) tan(34) =tan(43) är helt rimligt. Allt jag inte tänkte på det tidigare. Jag försökte lösa det hela men balansmetoden men jag får en negativ nämnare och positiv täljare så svaret kommer bli negativt. Jag vet att jag har gjort fel någon stans men förstår inte var..

Här blir det fel
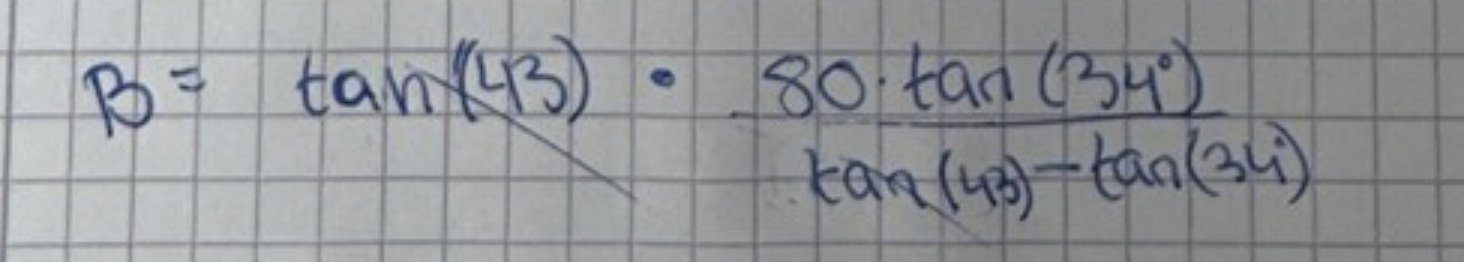
Sätt A=tan(43) och B=tan(34)
Vad som står här är
A * 80B/(A-B)
Det kan INTE bli
80B/B
Du kan inte förkorta tan(43) i täljaren emot en term i en differens i nämnaren.
Jag tror om du räknar om allt igen (även om början är perfekt), men redan i början inför
A=tan(43) och B=tan(34)
så tror jag räkningarna blir tydligare. Jag borde ha gjort det i min räkning. Det är inte bra att 'strula' runt med tan(43) och tan(34) så mycket. Till slut skriver man fel och de lömska författarna har valt 34 och 43, bara för att elever skall kasta runt siffrorna och förvilla sig. Med A och B blir allt mycket klarare och mindre risk för fel.
ja, just det. Man ska ju tänka att det är som en parantes runt täljare och nämnare när det är ett långt bråkstreck. Detta tänkte jag inte alls på. Jag ska testa igen :)
Trinity2 har bra råd. Det är lätt att skriva fel, så inför gärna korta beteckningar.
Jag föreslog tan(43) och tan(34), men man kan använda ännu enklare beteckningar.
Däremot tror jag inte att A och B är de bästa beteckningarna i en uppgift som redan innehåller a och b.
Äntligen kom jag fram till ett svar. Tog evigheter att förstå dig på den här uppgiften, som i själva fallet är ganska enkel. Men man tappar bara bort sig hela tiden. Jag skulle säga att det fortfarande punkter i min lösning som skulle kunna förbättras. Det var på gränsen till lite virrigt när man ersatte tan med variabler MEN långt ifrån lika jobbigt som när man hade allt utskrivet.
det är helt enkelt lättare att lösa uppgifter som denna och minimera risk för att saker blir fel om man använder sig av variabler så långt man kan.
 Tack för hjälpen till er alla, framförallt Trinity!😊
Tack för hjälpen till er alla, framförallt Trinity!😊