Beräkna koncentration vid jämvikt

Uppgiften är följande:

I ett kärl på $1.0 d m^{3}$ tillsätter vi $0.05357 m o l$ $N_{2} O_{4}$ och $0.193 m o l$ $N O_{2}$ det här gör att jämviktskonstanten för sönderfallet av $N_{2} O_{4}$ är $10.4 m o l / d m^{3}$ vid den aktuella temperaturen $T = 200 °$ .
Är systemet i jämvikt? Om inte, vad är koncentrationerna av $N_{2} O_{4}$ och $N O_{2}$ då jämvikten ställt in sig?

Hur kan jag gå tillväga för att beräkna koncentrationerna vid jämvikt då jag inte har koncentrationerna vid start?

Känner du till denna ekvation: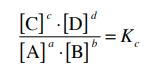

Om du skriver upp reaktionsformeln kan du dessutom uttrycka koncentrationen av ett ämne i termer av koncentrationen av det andra. På så sätt kan du lösa koncentrationen av det ena ämnet och med hjälp av molförhållandet beräkna koncentrationen av det andra.

Jag börjar med att ställa upp reaktionsformeln: $N_{2} O_{4} ⇄ N O_{2}$

Jag balanserar reaktionsformeln till: $N_{2} O_{4} ⇄ 2 N O_{2}$
Jag omvandlar substansmängderna för de båda ämnena med formeln: $c = \frac{n}{v}$

$c_{(N_{2} O_{4})} = \frac{0.05357}{1.0} = 0.5357$ $m o l / d m^{3}$
$c_{(N O_{2})} = \frac{0.193}{1.0} = 0.193 m o l / d m^{3}$

Jag sätter sedan in dessa koncentrationer i formeln för jämviktskonstanten:
$K_{c} = \frac{{[N O_{2}]}^{2}}{[N_{2} O_{4}]} = \frac{{(0.193)}^{2}}{(0.5357)} = 0.06953332089 m o l / d m^{3}$
Här kör jag sedan ihop, hur ska jag gå tillväga för att avgöra om det är i jämvikt? Och hur ska jag komma fram till koncentrationerna vid verklig jämvikt?

Formeln för jämviktskonstanten gäller endast då du vet att de två ämnena är i jämvikt. Nu räknar du med initialkoncentrationerna. Din beräkning av jämviktskonstanten i inlägg #3 överensstämmer alltså inte med den riktiga jämviktskonstanten (enligt uppgiften är den ju 10.4 mol/dm³). Så... är systemet i jämvikt?

Jag tänker så här då, för att ta reda på om systemet är i jämvikt så måste jag beräkna koncentrationskvoten, Q. Vid $200 °$ är systemets jämviktskonstant $K = 10.4 m o l / d m^{3}$ . Om systemet är i jämvikt så är kvoten mellan produkterna och reaktanternas koncentrationer $10.4$ .

$Q = \frac{{[N O_{2}]}^{2}}{[N_{2} O_{4}]} = \frac{{(0.193)}^{2}}{(0.5357)} = 0.06953332089 m o l / d m^{3}$

Då får jag att:

$Q < K$

Alltså, systemet är inte i jämvikt. Nettoreaktionen kommer fortsätta åt höger tills värdet blir lika stort som $K$ . Då har jag svarat på den frågan alltså, men hur tar jag fram koncentrationerna när denna jämvikt är uppnådd? Jag har värdet på $K$ , vid jämvikt men jag vet inget om koncentrationerna förutom mängden som tillsattes, jag behöver de ursprungliga värdena minus det tillsatta för att få koncentrationerna.

De ursprungliga värdena är de mängderna som tillsatts till bägaren (de givna substansmängderna).

Jaha, jag antog att om någonting tillsätts till något så måste det ha funnits något till att börja med, med andra ord så utgick jag från att kärlet redan innehöll en viss mängd x och y innan det tillsattes mer x och y. Men denna uppenbarelse hjälper mig dock inte att förstå hur jag kan kvantifiera ett uttryck som ger mig koncentrationerna vid uppnådd jämvikt.

Du har startkoncentrationerna, du kan sätta förändringen som av koncentrationen N₂O₄ som x och du vet K. Sätt upp en tabell med all data:

	N₂O₄	NO₂
initial	0.5357	0.193
förändning	- x	...
jämvikt	0.5357 - x	...

Kan du fylla i tabellen för NO₂?

	$N_{2} O_{4}$	$N O_{2}$
initial	0.5357	0.193
förändring	- x	+ x
jämvikt	0.5357 - x	0.193 + x

Så här? Är det inte relevant att inkludera den balanserade reaktionen?

Jag beräknade detta uttrycket: $10.4 = \frac{(0.193 + x)}{(0.5357 - x)}$ .
Om jag använder resultatet för x för att få koncentrationerna vid jämvikt och sedan sätta in dom i jämviktsekvationen för att verifiera mitt resultat som ska bli 10.4 så stämmer det inte. Och det känns generellt som att jag är på fel bana.

Det du fyllt i tabellen stämmer inte riktigt. Om x mol N₂O₄ reagerar, hur många mol NO₂ får du? I ditt uttryck bör koncentrationen NO₂ dessutom vara upphöjd till 2, som du skrev i inlägg #5.

	$N_{2} O_{4}$	$2 N O_{2}$
initial	$0.5357$	$0 . 193^{2}$
förändring	- x	2x
jämvikt	0.5357 - x	$0 . 193^{2} + 2 x$

Förhållandet är 1:2 mellan $N_{2} O_{4}$ och $2 N O_{2}$ .

Precis, rätt med förhållandet. Initialkoncentrationen är dock fortfarande 0.193, inte 0.193². I jämviktsekvationen får du använda parentes för koncentrationen NO₂. Då blir det:

$K = \frac{{(0.193 + 2 x)}^{2}}{0.5357 - x}$

Får du rätt svar nu?

$10.4 = \frac{{(0.193 + 2 x)}^{2}}{0.5357 - x}$

Jag flyttar över nämnaren till vänster om likhetstecknet:

$10.4 (0.5357 - x) = {(0.193 + 2 x)}^{2}$

Jag utvecklar båda leden:

$5.57 - 10.4 x = 4 x^{2} + 0.032249 5.57 = 4 x^{2} + 10.4 x + 0.032249 0 = 4 x^{2} + 10.4 x - 5.532751$

Sedan kör jag pq-formeln på formen: $a x^{2} + b x + c = 0$

$x = \frac{- b \pm \sqrt{b^{2}} - 4 a c}{2 a}$

$x_{1} = \frac{- 10.4 + \sqrt{10 . 4^{2}} - 4 \times 4 (- 5.32751)}{2 \times 4} x_{1} = \frac{- 10.4 + \sqrt{196.684016}}{8} x_{1} \approx 0.45$

då borde koncentrationerna vid jämvikt bli:

$N_{2} O_{4} = (0.5357 - 0.45) = 0.0857 m o l / d m^{3} 2 N O_{2} = (0.193 + 2 {(0.45))}^{2} = 1.195 m o l / d m^{3}$

Jag får den positiva roten till $x \approx 0.43$ när jag beräknar med miniräknarens ekvationslösare. Har du använt avrundade siffror när du beräknar rötterna?

Jag har inte gjort någon avrundning vid uträkningen och även om det skedde en avrundning så borde inte avvikelsen i svaret vara så stort som det du fick.

Nu inser jag att vi har räknar med koncentrationen 0.5357 mol/dm³ istället för 0.05357 mol/dm³ som det är i uppgiften... (ända från inlägg #3)

Jaha, det är lätt hänt då $\frac{0.193}{1.0} = 0.193$ så ser det ut som att vi arbetat med siffrorna innan konvertering från mol till $m o l / d m^{3}$ . Oavsett så känns det som att uppgiften är klar då koncentrationerna för de båda ämnena vid jämvikt är rimliga. Dock förstår jag inte varför frågan är formulerad på det sättet att de vill ha reda på koncentrationerna vid jämvikt när dom egentligen frågar om systemet är i jämvikt?

Svara

Visa senaste svar