Beräkna kondensatorns kapacitans
Hej,
Jag har lite problem med följande uppgift:
"En plattkondensator laddas ur genom en resistor på 600 Ω. Strömmen i kretsen är efter 3s en tredjedel av vad den var precis då urladdningen började.
Beräkna kondensatorns kapacitans."
Jag försökte med formeln för urladdning hos kondensatorer, se nedan. Men eftersom det inte finns några värden för spänningskällan eller för spänningen över kondensatorn fastnade jag. Är det någon som vet hur jag kan komma vidare? 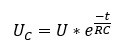
Du har att strömstyrkan efter 3s har sjunkigt till en tredjedel av vad den var vid "tid 0"
I en resistiv krets så är spänningen proportionell mot strömmen så om strömmen har fallit till en tredjedel så har spänningen också gjort det relativt vad den var från början
Det förhållandet ska räcka i kombination med urladdningsformeln för att bestämma kapacitansen men ta en stund och se om du kan gå från det där förhållandet närmare svaret.
Kalla spänningen från början för och räkna som om du visste det. Kör du fast igen, så visa hur långt du har kommit och fråga igen!
Okej så då har jag försökt med batterispänningen som 1 och spänningen över kondensatorn som 1/3. Tack så mycket för hjälpen!
Hej!
Kan du förklara hur du gjorde? Har en liknande fråga och kommer ingen vart.
Stars00 skrev:Hej!
Kan du förklara hur du gjorde? Har en liknande fråga och kommer ingen vart.
Välkommen till Pluggakuten!
Gör en ny tråd om din fråga, så blir det mindre rörigt än om du plockar upp en gammal zombie-tråd. Tänk på att ge tråden en bra rubrik och visa hur du har försökt själv. /moderator
Hej! jag ska bestämma en kapacitansen hos en kondensator och använder den angivna funktionen f(x)=A(1-e^-(1/RC)x
jag har konstanten A, som är 1.54, R = 10k ohm, nu måste jag räkna ut kapacitansen med hjälp av funktionen men hur gör jag det? Förstår inte hur man kommer vidare med beräkningen. Mycket tacksam för svar!
Starta en ny tråd för din fråga istället för att försöka väcka liv i den här gamla tråden.




