Beräkna kurvintegralen
Hej!
eftersom vektorfältet inte är definierad i origo så är det tydligen inte lämpligt att använda greens eller att hitta potentialfunktion. Hur brukar man hantera såna utmaningar? Området är ju slutet och begränsad.

Jag prövade att söka på nätet (då det var ett bra tag sedan jag sist löste sådana här uppgifter) och kom in på den här sidan från KTH.
Exempel 3 på sidan 3 där liknar din uppgift och där införde de polära koordinater. Det kanske kan funka.
Mina första tanke var att sluta området genom att gå längs med x-axeln till (-h,0), gå i en halvcirkel ovanför origo till (h,0) och sedan gå längs x-axeln till kurvans startposition, där 0<h<2. Och sedan använda Greens formel, men som sagt var det ett tag sedan jag sist löste sådana här uppgifter så det kanske inte gör saker och ting lättare.


Jag antar att du menar såhär? Jag hoppade direkt in på greens för att räkna ut något i termer av h och sen se när h närmar 0+
Greens formel får användas endast om kurvan är sluten. Den givna kurvan är inte det! Du behöver lägga till några kurvstycken för att få en sluten kurva och därmed kunna använda Greens formel. Sedan behöver du kompensera för att nya kurvstycken blivit tillagda till kurvintegralen.
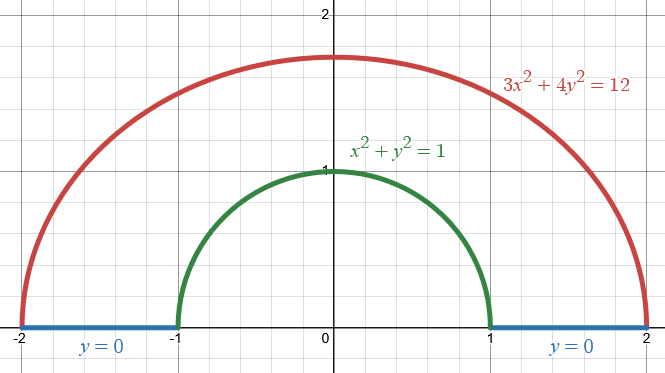
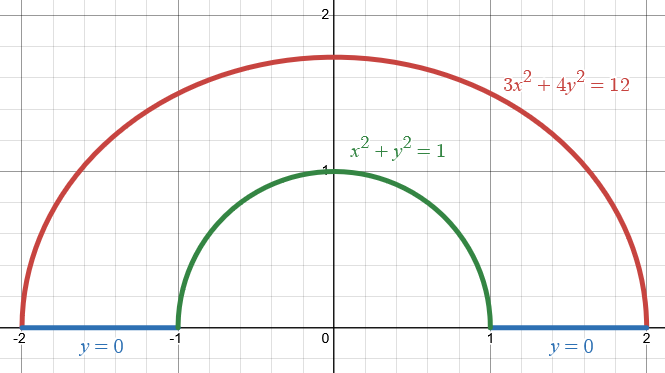
Området som innesluts av kurvan måste undvika origo eftersom det givna vektorfältet ej är kontinuerligt deriverbar i origo. Du kan göra som Bedinsis föreslagit, d.v.s. lägga till två vågräta sträckor och en halvcirkel (gärna enhetscirkeln), se figuren nedan:
Vektorfältets rotation är inte korrekt beräknad p.g.a. ett teckenfel - bråken och borde ha tagit ut varandra.
När jag följde exempel som bedinsis länkade så får jag detta. Notera att jag inte använde greens nu. Problemet är nu hur man ska integrera uttrycket i nämnaren


destiny99 skrev:När jag följde exempel som bedinsis länkade så får jag detta. Notera att jag inte använde greens nu.
[uträkning som slutar med en integral där man dividerar med 4*cos(t)^2+3*sin(t)^2]
4*cos(t)^2+3*sin(t)^2 = 1*cos(t)^2+3*cos(t)^2+3*sin(t)^2= 1*cos(t)^2+3*(cos(t)^2+sin(t)^2)= cos(t)^2+3
Formlerna för dubbla vinkeln brukar vara till nytta då man vill hitta primitiva funktionen till kvadraten av en trigonometrisk funktion. Jag ser dock ingen som kan appliceras.
Derivatan av arctan(x) är 1/(1+x^2) vilket liknar din integral. Det kanske går att göra en omskrivning med nya variabler.
Bedinsis skrev:destiny99 skrev:När jag följde exempel som bedinsis länkade så får jag detta. Notera att jag inte använde greens nu.
[uträkning som slutar med en integral där man dividerar med 4*cos(t)^2+3*sin(t)^2]
4*cos(t)^2+3*sin(t)^2 = 1*cos(t)^2+3*cos(t)^2+3*sin(t)^2= 1*cos(t)^2+3*(cos(t)^2+sin(t)^2)= cos(t)^2+3
Formlerna för dubbla vinkeln brukar vara till nytta då man vill hitta primitiva funktionen till kvadraten av en trigonometrisk funktion. Jag ser dock ingen som kan appliceras.
Derivatan av arctan(x) är 1/(1+x^2) vilket liknar din integral. Det kanske går att göra en omskrivning med nya variabler.
Yes såhär fick jag . Men är fortfarande lite fast. Detta liknar arctan men ändå inte för vi har u^2 eller liknande. Chatgpt föreslår en omskrivning av cos^2v som 1/1+tan^2v som tydligen ger samma sak

Hur blir det med de nya gränserna? Om vi sätter u=tanv? Tangens är väl ej definierad för 0 ?

LuMa07 skrev:Greens formel får användas endast om kurvan är sluten. Den givna kurvan är inte det! Du behöver lägga till några kurvstycken för att få en sluten kurva och därmed kunna använda Greens formel. Sedan behöver du kompensera för att nya kurvstycken blivit tillagda till kurvintegralen.
Området som innesluts av kurvan måste undvika origo eftersom det givna vektorfältet ej är kontinuerligt deriverbar i origo. Du kan göra som Bedinsis föreslagit, d.v.s. lägga till två vågräta sträckor och en halvcirkel (gärna enhetscirkeln), se figuren nedan:
Vektorfältets rotation är inte korrekt beräknad p.g.a. ett teckenfel - bråken och borde ha tagit ut varandra.
Facit använder faktiskt detta men jag fattar nada och vet inte hur man ska göra som dem. Sen förstår jag inte varför man tar y2-y1 ? Är det för att man får den där vita ytan där 0 inte är med?

Skall svaret bli
![]()
(Leker i MMA och undrar om jag skrivit rätt kommand...)
Trinity2 skrev:Skall svaret bli
(Leker i MMA och undrar om jag skrivit rätt kommand...)
Ja det är rätt! Så långt har jag kommit. Men jag vet inte hur jag ska få fram integralens värde mellan ellipsen och cirkeln dvs den vita ytan?

Du kan ju föra in polära koordinater för att få enkla integrationsgränser.
Bedinsis skrev:Du kan ju föra in polära koordinater för att få enkla integrationsgränser.
Men det står y1-y2. Vi har både en ellips och en cirkel så när du säger att jag ska införa polära koordinater där vi går från dxdy till r drdtheta så är det till ett område D
Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en cirkel?
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Jag antar att du menar såhär? Här är inre integralen en halvcirkel y2 och den yttre är ellipsen y1

destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Jag antar att du menar såhär? Här är inre integralen en halvcirkel y2 och den yttre är ellipsen y1
Nej,
INT_y2 – INT_y1
där y2=halvellips, y1=halvcirkel
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Jag antar att du menar såhär? Här är inre integralen en halvcirkel y2 och den yttre är ellipsen y1
Nej,
INT_y2 – INT_y1
där y2=halvellips, y1=halvcirkel
Okej jag kallade y2 för cirkeln och y1 för ellipsen.
destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Jag antar att du menar såhär? Här är inre integralen en halvcirkel y2 och den yttre är ellipsen y1
Nej,
INT_y2 – INT_y1
där y2=halvellips, y1=halvcirkel
Okej jag kallade y2 för cirkeln och y1 för ellipsen.
OK, bara man vet vad som är vad.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Jag antar att du menar såhär? Här är inre integralen en halvcirkel y2 och den yttre är ellipsen y1
Nej,
INT_y2 – INT_y1
där y2=halvellips, y1=halvcirkel
Okej jag kallade y2 för cirkeln och y1 för ellipsen.
OK, bara man vet vad som är vad.
Vilken av dessa skrivsätt är korrekta? Är båda korrekta?


destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Jag antar att du menar såhär? Här är inre integralen en halvcirkel y2 och den yttre är ellipsen y1
Nej,
INT_y2 – INT_y1
där y2=halvellips, y1=halvcirkel
Okej jag kallade y2 för cirkeln och y1 för ellipsen.
OK, bara man vet vad som är vad.
Vilken av dessa skrivsätt är korrekta? Är båda korrekta?
Det ena är linjeintegraler andra är ytintegraler.
Se till så att 2 kommer rätt.
Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Trinity2 skrev:destiny99 skrev:Bedinsis skrev:Försöker du inte räkna ut ytintegralen i över det inneslutna området?
Ja det är den vita området som gränsas mellan ellipsen som är y1 och cirkeln y2. Men jag vet inte om man subtrahera kurvorna från varandra för att få fram vad det är för område.
Är det bara
INT 2 dxdy
över y1-y2 är det lätt.
Tänk på att
INT 1 dxdy
är arean för y1-y2 och arean för en ellips är πab där a och b är halvaxlarna.
Nu kan du lätt beräkna integralen.
Nu förstår jag inte hur y1-y2 kan vara arean för en ellips?
Det är det inte men
INT_y1
är det, med a=2 och b=sqrt3 vilket ger arean 1/2 πab = sqrt3 π
Sedan är
INT_y2 = halvcirkel = π/2
Alltså är intergralen
2 ( sqrt3π-π/2) = (2sqrt3-1)π
Så området är alltså arean av ellips minus arean av en halvcirkel?
en halvellips-halvcirkel
Okej om man inte hade kommit på detta på grund av glömska eller blackout , hade man kunnat gå parametrisering vägen med polära koordinater som bedinsis var inne på och sånt ? Hur hade man gjort för y1 och y2 isåfall?
Går utmärkt. Den inre är en halvcirkel så det är tveksamt att man beräknat denna med en integral, vi glömmer sällan arean av en cirkel. Den andra är bara att parameterisera och räkna på. Prova att bevisa formeln A=πab för en ellips.
Jag antar att du menar såhär? Här är inre integralen en halvcirkel y2 och den yttre är ellipsen y1
Nej,
INT_y2 – INT_y1
där y2=halvellips, y1=halvcirkel
Okej jag kallade y2 för cirkeln och y1 för ellipsen.
OK, bara man vet vad som är vad.
Vilken av dessa skrivsätt är korrekta? Är båda korrekta?
Det ena är linjeintegraler andra är ytintegraler.
Se till så att 2 kommer rätt.
Aa ok. Jaha du menar konstanten 2? Ja den är utanför och jag missade att ha stor parentesen för ytintegralen. Tack!
Hej, glöm inte att du har de två linjesegmenten längs med x-axeln kvar. Dessa ingår ju också i randen till ditt område. Dessa måste också redovisad för korrekt lösning. Just i det här fallet så blir dessa integraler noll, så svaret blir samma. Men på en tenta så blir det mycket poängavdrag om du missar det.
jamolettin skrev:Hej, glöm inte att du har de två linjesegmenten längs med x-axeln kvar. Dessa ingår ju också i randen till ditt område. Dessa måste också redovisad för korrekt lösning. Just i det här fallet så blir dessa integraler noll, så svaret blir samma. Men på en tenta så blir det mycket poängavdrag om du missar det.
Hej! Jag vet inte vilka två linjesegment du syftar på och vad jag ska ta med för att få poäng när lösningsförslaget inte ens tog med två linjesegment längs x-axeln i sin redovisning? Jag la inte ens märke till dem och förstår inte varför de skall tas med som en del av redovisning. Får nog återkomma med svar om det blir poängavdrag eller inte när jag hört med andra. Jag har tyvärr inte så bra koll själv.
Om inte linjesegmenten är med får du inget slutet område. Då kan du inte använda Green's helt enkelt.
Om du vill slippa linjesegmenten så kan du alternativt sluta området med övre halvan av cirkeln med radie 2.
Edit. Linjesegmenten jag menar är de som Bedinsis pratar om i #2
jamolettin skrev:Om inte linjesegmenten är med får du inget slutet område. Då kan du inte använda Green's helt enkelt.
Om du vill slippa linjesegmenten så kan du alternativt sluta området med övre halvan av cirkeln med radie 2.
Hur menar du då? Att den vita ytan inte är slutet område?
Vilken yta menar du är vit? Jag menar området som du ritat i din lösning.
jamolettin skrev:Vilken yta menar du är vit? Jag menar området som du ritat i din lösning.
Jag menar området som är mellan ellipsen och cirkeln med radie 1. Jag ritade denna bild nu för att försöka matcha med det du skrev innan. Området verkar vara slutet nu. Den gröna är ellipsen med y1 och den lilla är y2 med cirkeln med radie 2.

Nej, det är inget slutet område.
jamolettin skrev:Nej, det är inget slutet område.
Ah okej då tror jag inte jag är med riktigt på hur du menar.
Du skriver cirkel med radie 1 och sedan cirkel med radie 2. Menar du olika cirklar?
jamolettin skrev:Du skriver cirkel med radie 1 och sedan cirkel med radie 2. Menar du olika cirklar?
Nej den ena är ellips med radie 2 och den andra är en cirkel med radie 2. Förut hade jag en cirkel med radie 1 och en ellips med radie 2. Jag försökte bara göra som du sa på följande sätt nedan i #35

Ja, då blir området slutet utan linjesegmenten.
jamolettin skrev:Ja, då blir området slutet utan linjesegmenten.
Facit hade en sån bild med linjesegment y1 och y2. De ska inte vara med menar du?

På bilden ser jag ett cirkelsegment och ett ellipssegment. Ett linjesegment är en del av en rät linje som jag ser det.
Det förklarar ju i alla fall varför vi missförstått varandra hela tiden..., lycka till nu med dina studier.
jamolettin skrev:På bilden ser jag ett cirkelsegment och ett ellipssegment. Ett linjesegment är en del av en rät linje som jag ser det.
Det förklarar ju i alla fall varför vi missförstått varandra hela tiden..., lycka till nu med dina studier.
Ja det är inte helt lätt med kommunikationen här ibland. Vad bra! Tack snälla.