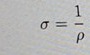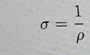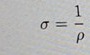Beräkna ledningsförmåga

kanske kan den här länken bidra?

https://sv.wikipedia.org/wiki/Elektrisk_konduktivitet

Det borde stå något om ledningsförmåga eller konduktivitet i din kurslitteratur.

Ture skrev:

kanske kan den här länken bidra?

https://sv.wikipedia.org/wiki/Elektrisk_konduktivitet

Det borde stå något om ledningsförmåga eller konduktivitet i din kurslitteratur.

Nej det gör det inte och allt är på engelska tyvärr. I wikipedia ser det ut som att resistivitet är det de menae med ledningsförmåga ?

destiny99 skrev:

Nej det gör det inte och allt är på engelska tyvärr. I wikipedia ser det ut som att resistivitet är det de menae med ledningsförmåga ?

 

resistivitet och konduktivitet hänger ihop enligt formeln:

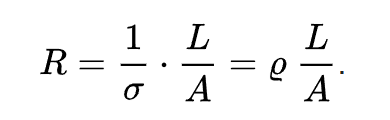
Där R är resistansen 

sigma konduktiviteten

L är ledarens längd

A ledarens tvärsnittsarea

rå är resistiviteten.

Så om du räknar ut resistiviteten får du konduktiviteten som 1/resistiviteten

Även om din kurslitteratur är på engelska måste begreppen konduktivitet, resistivitet, konduktans och resistans behandlas.

har du kollat i registret efter dessa ord?: conductivity, resistivity, conductance and resistance

destiny99 skrev:

För att mäta ledningsförmågan i saltvatten (och därigenom indirekt salthalten) använder man sig av två koncentriska cylindrar där den inre har diametern 10 cm och den yttre har diametern 60 cm. Båda cylindrarna är 50 cm långa och man mäter upp en resistans mellan dem på 114 ohm när de är nedsänkta i havsvatten. Vilken ledningsförmåga (uttryckt i S/m) har havsvattnet?  

Jag tänker endast på den där formeln $R=\frac{\rho L }{A}$

Den formeln funkar inte för den här radiella geometrin. Vet du hur du bestämmer $\varrho$ för en koaxial cylinder?

Sedan är det bara att specifik ledningsförmåga $\sigma = 1/\varrho$.

Pieter Kuiper skrev:

destiny99 skrev:

För att mäta ledningsförmågan i saltvatten (och därigenom indirekt salthalten) använder man sig av två koncentriska cylindrar där den inre har diametern 10 cm och den yttre har diametern 60 cm. Båda cylindrarna är 50 cm långa och man mäter upp en resistans mellan dem på 114 ohm när de är nedsänkta i havsvatten. Vilken ledningsförmåga (uttryckt i S/m) har havsvattnet?  

Jag tänker endast på den där formeln $R=\frac{\rho L }{A}$

Den formeln funkar inte för den här radiella geometrin. Vet du hur du bestämmer $\varrho$ för en koaxial cylinder?

Sedan är det bara att specifik ledningsförmåga $\sigma = 1/\varrho$.

Nej jag vet inte. Men lösningsförslaget valde  de att integrera vilket jag inte förstår. Varför funkar inte denna formel jag tänkte på ovan? 

Just denna formel sigma=1/rho hittar jag inte i boken. 

destiny99 skrev:

Pieter Kuiper skrev:

Visa föregående citat

destiny99 skrev:

För att mäta ledningsförmågan i saltvatten (och därigenom indirekt salthalten) använder man sig av två koncentriska cylindrar där den inre har diametern 10 cm och den yttre har diametern 60 cm. Båda cylindrarna är 50 cm långa och man mäter upp en resistans mellan dem på 114 ohm när de är nedsänkta i havsvatten. Vilken ledningsförmåga (uttryckt i S/m) har havsvattnet?  

Jag tänker endast på den där formeln $R=\frac{\rho L }{A}$

Den formeln funkar inte för den här radiella geometrin. Vet du hur du bestämmer $\varrho$ för en koaxial cylinder?

Sedan är det bara att specifik ledningsförmåga $\sigma = 1/\varrho$.

Nej jag vet inte. Men lösningsförslaget valde  de att integrera vilket jag inte förstår. Varför funkar inte denna formel jag tänkte på ovan? 

Just denna formel sigma=1/rho hittar jag inte i boken. 

Där var den ju!

Sedan hade du alltså facit.

Uppgiften handlar alltså om motståndet mellan insida och utsida av en cylindermantel. Inte om motståndet mellan änderna. En helt annan geometri. Jo, det är lämpligt att lösa genom integrering med tunna skal av tjockleken dr.

Pieter Kuiper skrev:

destiny99 skrev:

Visa föregående citat

Pieter Kuiper skrev:

destiny99 skrev:

För att mäta ledningsförmågan i saltvatten (och därigenom indirekt salthalten) använder man sig av två koncentriska cylindrar där den inre har diametern 10 cm och den yttre har diametern 60 cm. Båda cylindrarna är 50 cm långa och man mäter upp en resistans mellan dem på 114 ohm när de är nedsänkta i havsvatten. Vilken ledningsförmåga (uttryckt i S/m) har havsvattnet?  

Jag tänker endast på den där formeln $R=\frac{\rho L }{A}$

Den formeln funkar inte för den här radiella geometrin. Vet du hur du bestämmer $\varrho$ för en koaxial cylinder?

Sedan är det bara att specifik ledningsförmåga $\sigma = 1/\varrho$.

Nej jag vet inte. Men lösningsförslaget valde  de att integrera vilket jag inte förstår. Varför funkar inte denna formel jag tänkte på ovan? 

Just denna formel sigma=1/rho hittar jag inte i boken. 

Där var den ju!

Sedan hade du alltså facit.

Uppgiften handlar alltså om motståndet mellan insida och utsida av en cylindermantel. Inte om motståndet mellan änderna. En helt annan geometri. Jo, det är lämpligt att lösa genom integrering med tunna skal av tjockleken dr.

Jo men den formeln hittar jag inte i boken.  Men det är bra att det finns i wikipedia så vet man.

Pieter Kuiper skrev:

destiny99 skrev:

Visa föregående citat

Pieter Kuiper skrev:

destiny99 skrev:

För att mäta ledningsförmågan i saltvatten (och därigenom indirekt salthalten) använder man sig av två koncentriska cylindrar där den inre har diametern 10 cm och den yttre har diametern 60 cm. Båda cylindrarna är 50 cm långa och man mäter upp en resistans mellan dem på 114 ohm när de är nedsänkta i havsvatten. Vilken ledningsförmåga (uttryckt i S/m) har havsvattnet?  

Jag tänker endast på den där formeln $R=\frac{\rho L }{A}$

Den formeln funkar inte för den här radiella geometrin. Vet du hur du bestämmer $\varrho$ för en koaxial cylinder?

Sedan är det bara att specifik ledningsförmåga $\sigma = 1/\varrho$.

Nej jag vet inte. Men lösningsförslaget valde  de att integrera vilket jag inte förstår. Varför funkar inte denna formel jag tänkte på ovan? 

Just denna formel sigma=1/rho hittar jag inte i boken. 

Där var den ju!

Sedan hade du alltså facit.

Uppgiften handlar alltså om motståndet mellan insida och utsida av en cylindermantel. Inte om motståndet mellan änderna. En helt annan geometri. Jo, det är lämpligt att lösa genom integrering med tunna skal av tjockleken dr.

Aa ok då förstår jag