Beräkna linjeintegralen
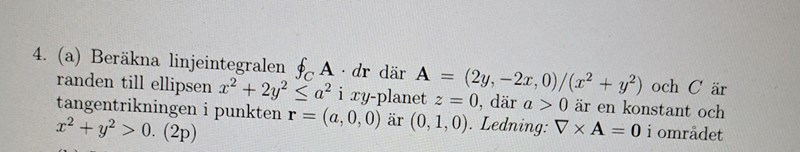

Stokes sats kan inte användas här pga fältet är definierad kring origo. Men jag stötte på ett problem när jag ska integrera uttrycket på slutet. Hur integrerar man när man har 1+cos^2t i nämnaren? Finns det kanske en annan väg så man slipper integrera trigonometrisk uttryck i nämnaren?
Det går att lösa uppgiften på det sätt du påbörjat, men det leder till krångliga räkningar och jag tror det är tänkt att du ska öva på Stokes sats här.
Försök använda Stokes sats genom att lägga en cirkel runt origo och välj en listig integrationsväg som gör att du räknar på områden som inte innehåller singulariteten. Börja med att skissa en bild över integrationsområdet, märk ut åt vilket håll linjeintegralen går (tangentriktningen för kurvan).
Använd gärna polära koordinater.
D4NIEL skrev:Det går att lösa uppgiften på det sätt du påbörjat, men det leder till krångliga räkningar och jag tror det är tänkt att du ska öva på Stokes sats här.
Försök använda Stokes sats genom att lägga en cirkel runt origo och välj en listig integrationsväg som gör att du räknar på områden som inte innehåller singulariteten. Börja med att skissa en bild över integrationsområdet, märk ut åt vilket håll linjeintegralen går (tangentriktningen för kurvan).
Använd gärna polära koordinater.
Ok. Men hur kan man använda stokes sats när det är odefinierad kring origo? Vilket integrationsområde ska jag rita?
Börja med att rita upp ellipsen . Märk ut huvudaxlarna. Skriv sedan in en maximal cirkel med centrum i origo. Vilken radie kan cirkeln maximalt ha för att fortfarande få plats in din ellips?
Slutligen, markera integrationsvägen för linjeintegralen med riktning och fundera över om det finns smarta vägar att bilda slutna områden där utan att punkten (0,0) ligger i området.
D4NIEL skrev:Börja med att rita upp ellipsen . Märk ut huvudaxlarna. Skriv sedan in en maximal cirkel med centrum i origo. Vilken radie kan cirkeln maximalt ha för att fortfarande få plats in din ellips?
Slutligen, markera integrationsvägen för linjeintegralen med riktning och fundera över om det finns smarta vägar att bilda slutna områden där utan att punkten (0,0) ligger i området.
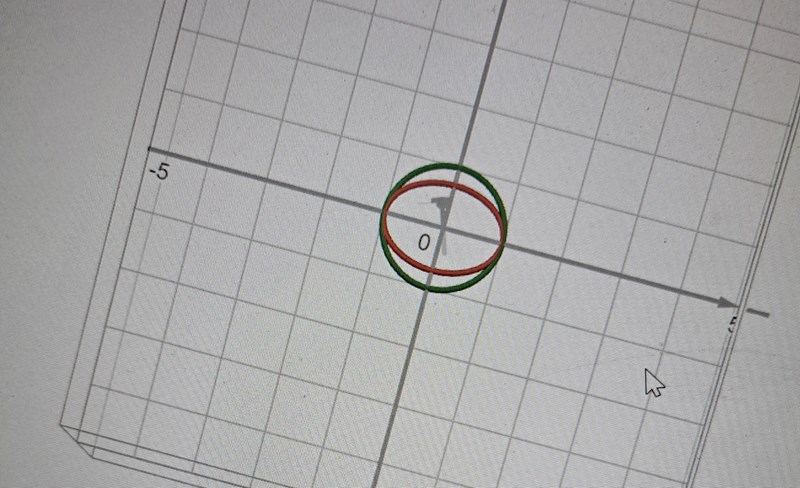
Den gröna är x^2+y^2=1 och den röda är x^2+2y^2=a^2
Mm, men vi vill att cirkeln ska få plats helt inuti ellipsen. Just nu sticker ju den gröna cirkeln ut utanför den röda ellipsen!
Sedan kan du markera integrationsriktningen (den väg linjeintegralen ska gå runt den röda ellipsen)
D4NIEL skrev:Mm, men vi vill att cirkeln ska få plats helt inuti ellipsen. Just nu sticker ju den gröna cirkeln ut utanför den röda ellipsen!
Sedan kan du markera integrationsriktningen (den väg linjeintegralen ska gå runt den röda ellipsen)
Ja jag har fastnat på hur du menar att det ska se ut. Jag undrar varför vi ska rita en cirkel över huvudtaget inuti en ellips ? Jag tror inte jag är med riktigt.
Orsaken till att du fick krångliga räkningar är att du räknar på en ellips, de ger krångliga linjeintegraler.
Vi ska försöka utnyttja att och Stokes sats för att få enklare integraler.
Får att få använda Stokes sats får dock inte punkten (0,0) vara med i något integrationsområde.
Tanken med din skiss är att du ska se integrationsområdet och förstå vad som menas med att "tangentriktningen i punkten är ".
Med en skiss är det också lättare att få idéer om hur du kan välja dina integrationsvägar så att de omsluter områden som inte innehåller punkten (0,0).
Cirkeln var bara en ledtråd om möjliga integrationsvägar, cirklelbågar är _mycket_ lättare att räkna på än ellipser.
D4NIEL skrev:Orsaken till att du fick krångliga räkningar är att du räknar på en ellips, de ger krångliga linjeintegraler.
Vi ska försöka utnyttja att och Stokes sats för att få enklare integraler.
Får att få använda Stokes sats får dock inte punkten (0,0) vara med i något integrationsområde.
Tanken med din skiss är att du ska se integrationsområdet och förstå vad som menas med att "tangentriktningen i punkten är ".
Med en skiss är det också lättare att få idéer om hur du kan välja dina integrationsvägar så att de omsluter områden som inte innehåller punkten (0,0).
Cirkeln var bara en ledtråd om möjliga integrationsvägar, cirklelbågar är _mycket_ lättare att räkna på än ellipser.
Såhär tänker jag mig om cirkeln x^2+y^2=R^2 ska ligga inuti ellipsen där R>0 . Om vi ska undvika origo så är det bäst att integrera längs med randen till cirkeln istället för punkterna inuti cirkeln där origo kan vara en av dem. Hur ska man veta att rotationen är 0 om vi väljer tex x^2+y^2=R^2 ? En annan sak som jag undrar över är varför cirkeln är inuti ellipsen och varför den inte får vara utanför?
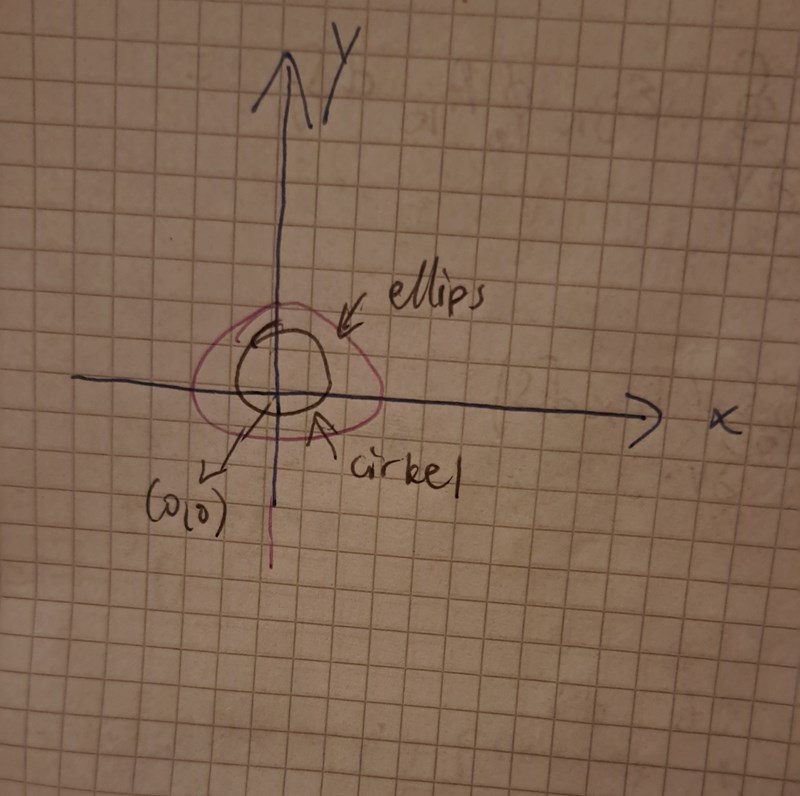
Tips.
PATENTERAMERA skrev:Tips.
Jag förstår tyvärr inte din figur.
Det viktiga är att du bildar ett eller flera sammanhängande områden som utesluter punkten i centrum där fältet är singulärt.
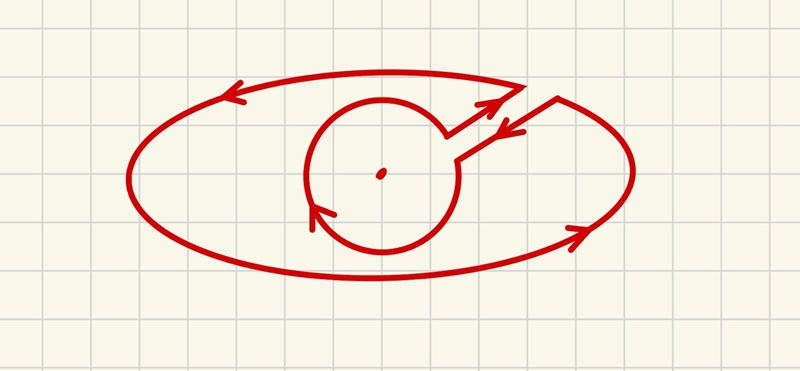
Här är en annan idé där vi bildar ett sammanhängande blått område där Stokes sats gäller för randkurvorna och området (halva ellipsen och halva cirkeln). Men du behöver såklart två sådana områden för att täcka in hela ellipsbågen.
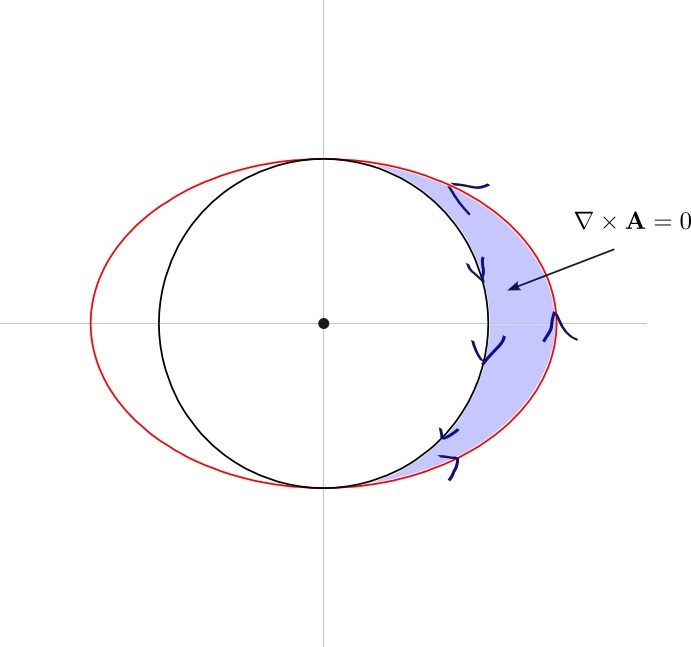
D4NIEL skrev:Det viktiga är att du bildar ett eller flera sammanhängande områden som utesluter punkten i centrum där fältet är singulärt.
Här är en annan idé där vi bildar ett sammanhängande blått område där Stokes sats gäller för randkurvorna och området (halva ellipsen och halva cirkeln). Men du behöver såklart två sådana områden för att täcka in hela ellipsbågen.
Om man väljer cirkeln,så slipper man singulära punkten där fältet är odefinierad. Men var kommer (a,0,0) och (0,1,0) in här?
(a,0,0) är en punkt på din ellips.
(0,1,0) är en tangentriktning; det är en vektor som pekar åt vilket håll linjeintegralen går (integrationsriktning medurs eller moturs).


