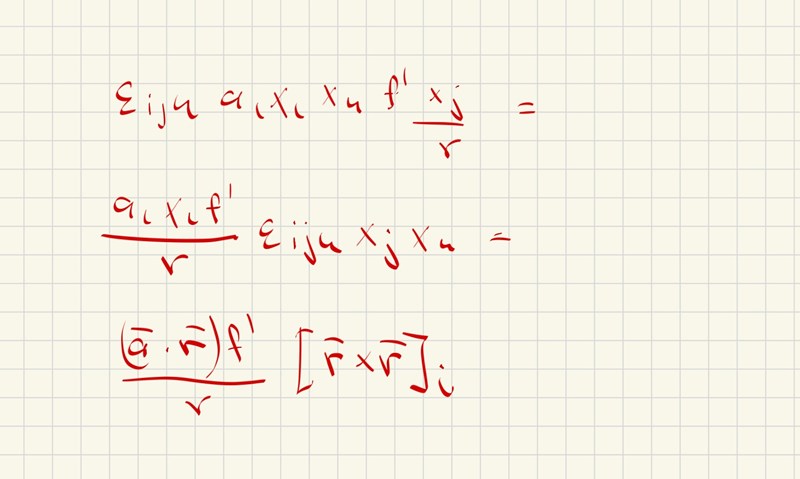Beräkna nabla kryss A
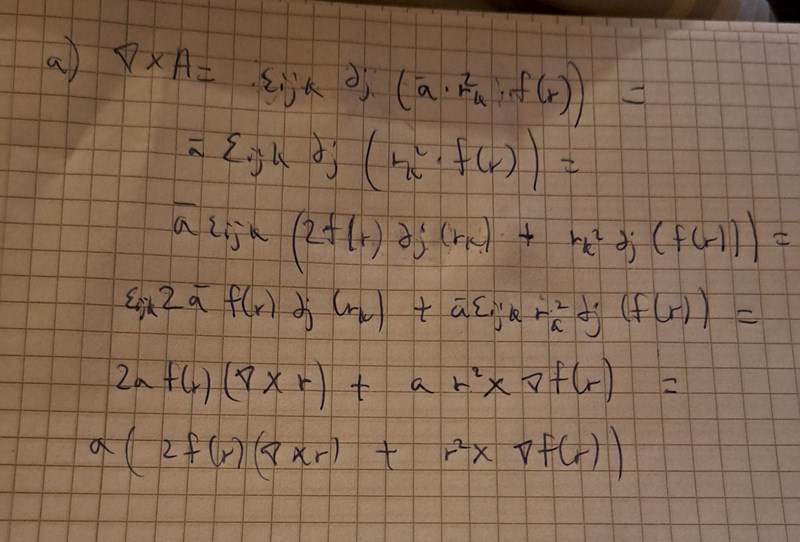
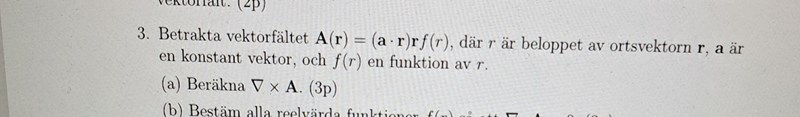
I a) uppgiften stämmer inte mitt slutgiltiga svar och jag tror det är pga indexräkning. Hur korrigerar jag detta utifrån min lösning ovan?
[(a•r)r]k = amxmxk.
Sedan så gäller det att f,j = (df/dr)xj/r.
PATENTERAMERA skrev:[(a•r)r]k = amxmxk.
Sedan så gäller det att f,j = (df/dr)xj/r.
varför är det amxmxk? Var kommer xk och xm ifrån?
Den andra är jag inte med på.
xi är i:te komponenten till r. Det är bättre att skriva xi istället för ri eftersom det lätt kan bli hopblandning mellan r och ri annars.
PATENTERAMERA skrev:.
Ok så det är xj komponenten av ortsvektorn r? Men varför delar man xj med r? Hur vet du att r=sqrt(x1^2+y^2+z^2)?
PATENTERAMERA skrev:xi är i:te komponenten till r. Det är bättre att skriva xi istället för ri eftersom det lätt kan bli hopblandning mellan r och ri annars.
Ja ok. Men du har inte förklarat varför man sätter index på a? Jag trodde den var en konstant vektor. Vad är tumregeln här? Sen undrar jag också varför xm och am har samma index.
destiny99 skrev:PATENTERAMERA skrev:.
Ok så det är xj komponenten av ortsvektorn r? Men varför delar man xj med r? Hur vet du att r=sqrt(x1^2+y^2+z^2)?
Det står i texten att r är beloppet av r.
destiny99 skrev:PATENTERAMERA skrev:xi är i:te komponenten till r. Det är bättre att skriva xi istället för ri eftersom det lätt kan bli hopblandning mellan r och ri annars.
Ja ok. Men du har inte förklarat varför man sätter index på a? Jag trodde den var en konstant vektor. Vad är tumregeln här? Sen undrar jag också varför xm och am har samma index.
a är en konstant vektor. Eftersom den är en vektor så skall den ha ett index när du använder indexnotation. a•r = amxm. Det är en skalärprodukt mellan a och r.
PATENTERAMERA skrev:destiny99 skrev:PATENTERAMERA skrev:.
Ok så det är xj komponenten av ortsvektorn r? Men varför delar man xj med r? Hur vet du att r=sqrt(x1^2+y^2+z^2)?
Det står i texten att r är beloppet av r.
Ok den delen har jag förstått eftersom vi utför rotation av A så måste ju r vara en ortsvektor i 3D och dess belopp blir ju sqrt(...). Men jag undrar hur man ska hantera den här sista termen?
PATENTERAMERA skrev:destiny99 skrev:PATENTERAMERA skrev:xi är i:te komponenten till r. Det är bättre att skriva xi istället för ri eftersom det lätt kan bli hopblandning mellan r och ri annars.
Ja ok. Men du har inte förklarat varför man sätter index på a? Jag trodde den var en konstant vektor. Vad är tumregeln här? Sen undrar jag också varför xm och am har samma index.
a är en konstant vektor. Eftersom den är en vektor så skall den ha ett index när du använder indexnotation. a•r = amxm. Det är en skalärprodukt mellan a och r.
Ah ok då är jag med.
PATENTERAMERA skrev:=…
Du verkar ha missat min figur i #10. Enligt facit så kommer den sista termen att inte överleva och jag vill förstå vad som händer med den , det steget har de hoppat över.
Nej, men jag förstår inte hur du kom fram till detta. Jag visade hur man skall börja.
PATENTERAMERA skrev:
Nej, men jag förstår inte hur du kom fram till detta. Jag visade hur man skall börja.
Jag skrev bara hur facit gjorde vilket är samma som du försökte börja med. Jag vet inte vad du inte förstår. Så jag postar hela min utskrivna lösning från facit. Den sista termen på sista raden överlever som sagt inte enligt facit och jag förstår inte varför( de hoppar över det steget). Jag markerade den termen med lila färg.

OK, som du ser så är det något konstigt med sista termen eftersom j förekommer tre gånger.
På din tredje rad så har du skrivit . Det skall bara vara .
Sedan gäller det att .
PATENTERAMERA skrev:OK, som du ser så är det något konstigt med sista termen eftersom j förekommer tre gånger.
På din tredje rad så har du skrivit . Det skall bara vara .
Sedan gäller det att .
Ok jag är tyvärr inte bra på hur man hanterar dj (f(r)) med index. Så jag får acceptera det korrekta sättet och som du säger j får inte förekomma mer än två gånger.
Ok nu har jag korrigerat detta efter vad du skrev i #16.
Det är en form av kedjeregel.
. F är en reellvärd funktion av en reell variabel. är ett skalärfält.
Då gäller att
.
I vårt fall så är F = f. Och .
Sedan får du utnyttja att epsilon är antisymmetrisk i sina index och att det efterföljande uttrycket är symmetriskt i j och k. Det betyder att det blir noll.
PATENTERAMERA skrev:Sedan får du utnyttja att epsilon är antisymmetrisk i sina index och att det efterföljande uttrycket är symmetriskt i j och k. Det betyder att det blir noll.
Det där förstår jag tyvärr inte hur du menar och hur jag ska hantera detta nedan. Jag är med på att eijk=-ejik pga antisymmetri , men är ej med på vad som blir 0 och vad du menar är symmetrisk.

Symmetri/antisymmetri är ett sätt att se det.
Men du kan även se vad uttrycket blir när du skriver om till vektornotation.
. Där vi inser att kryssprodukten blir noll.
PATENTERAMERA skrev:Symmetri/antisymmetri är ett sätt att se det.
Men du kan även se vad uttrycket blir när du skriver om till vektornotation.
. Där vi inser att kryssprodukten blir noll.
Nja jag ser tyvärr inte vad rxr/r blir för något
; en vektor kryssad med sig själv blir alltid noll.
PATENTERAMERA skrev:; en vektor kryssad med sig själv blir alltid noll.
Något som även förvirrar mig är när man har först xk kryss df/dr*(xj/r). Jag vet inte vad xk , xj och r är för något så att allt blir 0. Det är många variabler att hålla koll på och alla betyder olika saker.
PATENTERAMERA skrev:
Ok jag förstår tyvärr inte detta och det besvarar inte mina frågor i inlägget innan. Jag upprepar vad jag undrar om.
1) Vad står xk för ?
2) vad står xj för?
3) vad står r för ?
4) vad står xl för ?
5) vilken koppling har alla dessa variabler till varandra?
xm är den m:te komponenten av ortsvektorn r. (xm = r•em).
r är beloppet av ortsvektorn. r = |r|.
Förstår inte vad du menar med fråga 5).
PATENTERAMERA skrev:xm är den m:te komponenten av ortsvektorn r. (xm = r•em).
r är beloppet av ortsvektorn. r = |r|.
Förstår inte vad du menar med fråga 5).
Så xm är tex m=1,2,3 av komponenterna i ortsvektorn r=x+y+z? Då är alltså xk och xj samma komponenter i samma ortsvektorn fast med olika index?
r = (x1, x2, x3)
PATENTERAMERA skrev:r = (x1, x2, x3)
En ortsvektor är väl summan av dessa? x1, x2 och x3 är väl x, y och z?
Nej. Då blir det en skalär och inte en vektor.
PATENTERAMERA skrev:Nej. Då blir det en skalär och inte en vektor.
Ok. Så om r är en beloppet av ortsvektorn r så varför skriver man xj/r?
Du har inte svarat på mina frågor om xk och xj. Varför är det samma komponenter av ortsvektorn r?
destiny99 skrev:PATENTERAMERA skrev:Nej. Då blir det en skalär och inte en vektor.
Ok. Så om r är en beloppet av ortsvektorn r så varför skriver man xj/r?
, där vi utnyttjar att .
destiny99 skrev:Du har inte svarat på mina frågor om xk och xj. Varför är det samma komponenter av ortsvektorn r?
xk är k:te komponenten och xj är j:te komponenten förstås.
PATENTERAMERA skrev:destiny99 skrev:Du har inte svarat på mina frågor om xk och xj. Varför är det samma komponenter av ortsvektorn r?
xk är k:te komponenten och xj är j:te komponenten förstås.
De tillhör samma ortsvektor r när man utför kryss produkt vilket är som att säga att (x1,x2,x3)×(x1,x2,x3) eller hur?
PATENTERAMERA skrev:destiny99 skrev:PATENTERAMERA skrev:Nej. Då blir det en skalär och inte en vektor.
Ok. Så om r är en beloppet av ortsvektorn r så varför skriver man xj/r?
, där vi utnyttjar att .
Jag förstår inte varför man delar med r här och vad r är här. Kan du visa ett exempel där detta gäller?
r är hela tiden beloppet av ortsvektorn.


Tillägg: 7 dec 2025 12:36
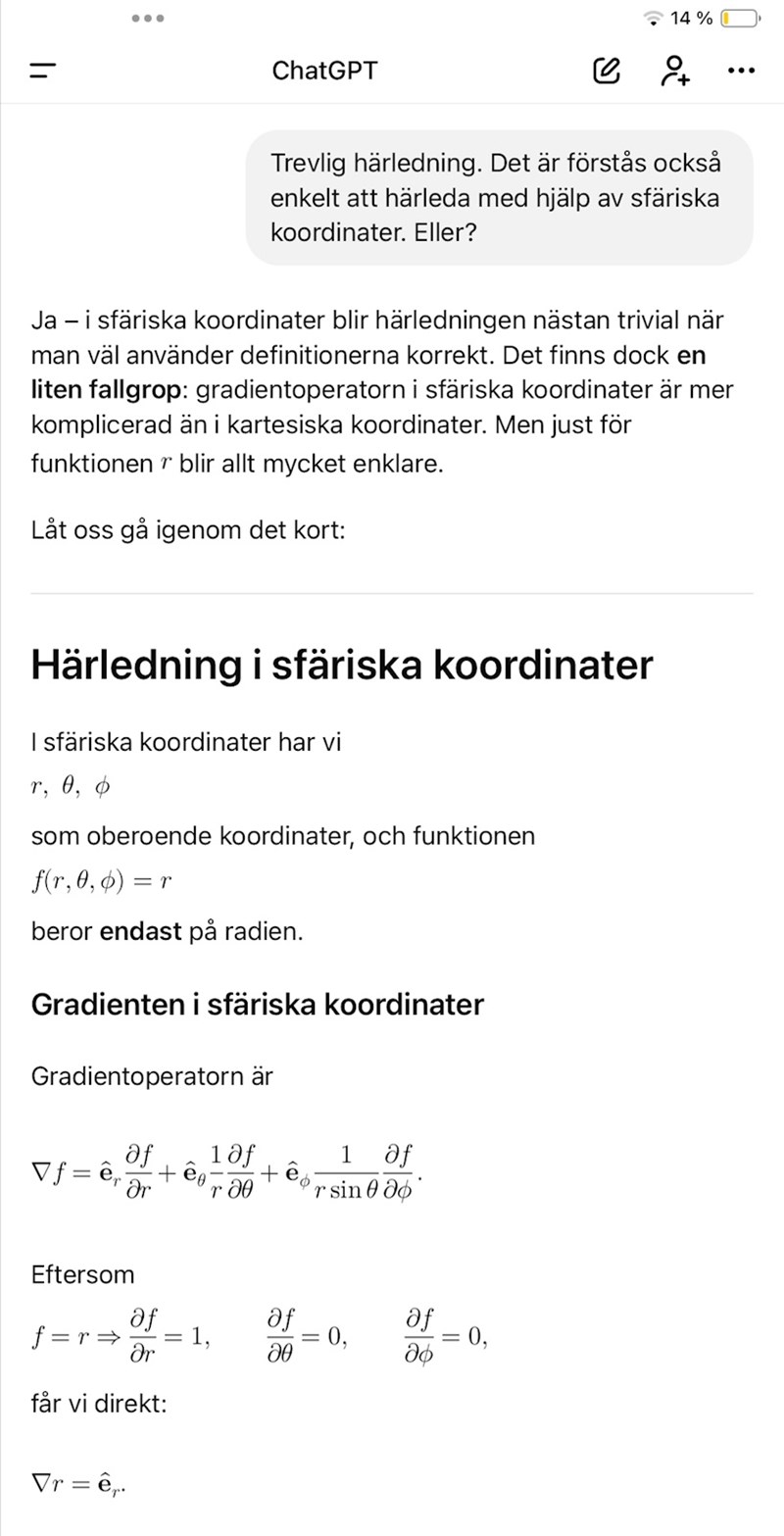
PATENTERAMERA skrev:r är hela tiden beloppet av ortsvektorn.
Jag tolkar som att r är beloppet av ortsvektorn , så när man deriverar f(r) så är det som att derivera f(sqrt(x1^2+x^2+x3^2)) map på r (beloppet) och mha kedjeregeln får man ju f'(r)*x1/r , f'(r)*x2/r eller f'(r)*x3/r beroende på om vill derivera x1 , x2 eller x3. Det chat säger förstår jag.
Kan du även svara på #37 ?
Ja, precis.
#37: korrekt.