beräkna olikheter
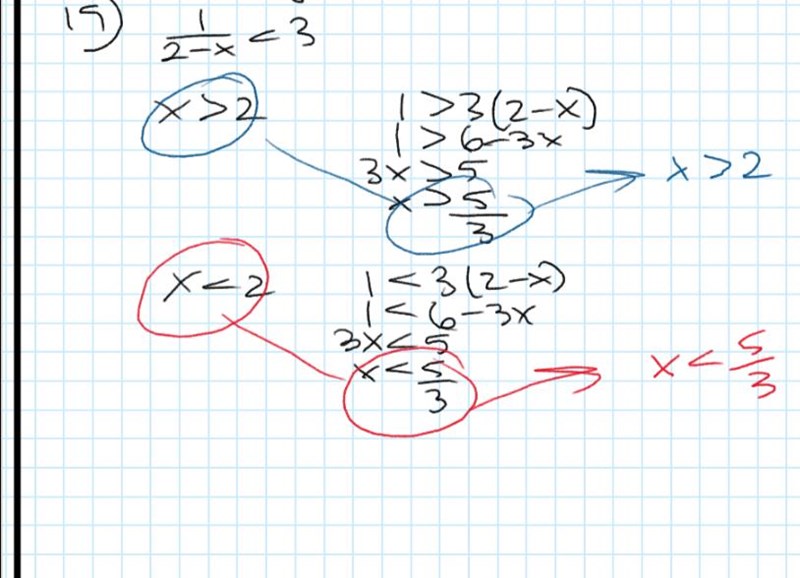
Varför blir fall 1 x>2 medans fall 2 blir x<5/3
Repetition av Ma1:
Om så förlänger du med ett positivt tal, när du multiplicerar båda sidorna med 2-x.
Om så förlänger du med ett negativt tal, när du multiplicerar båda sidorna med 2-x. Då måste du vända på olikheten.
ja. det är ju det jag har gjort. Men varför blir det som är inringat i blått x>2 medans det fallet som är inringat i rött då blir svaret det man räknat ut dvs x<5/3
solaris skrev:ja. det är ju det jag har gjort. Men varför blir det som är inringat i blått x>2 medans det fallet som är inringat i rött då blir svaret det man räknat ut dvs x<5/3
För att båda de inringade blåa olikheterna ska vara sanna.
Har du ritat in dina svar på en tallinje? Då ser du att en gräns hamnar på fel sida om en annan gräns för att det skall spela någon roll.
Om du vet att så fungerar ju inte , eftersom det x-värdet är mindre än 2.
Det betyder att påståendet inte stämmer för , men att det stämmer både för större och för mindre tal.
Om du ritar upp de båda funktionerna och så ser du tydligt vilken av kurvorna som har störst y-värde för varje x-värde.



