beräkna områdets area
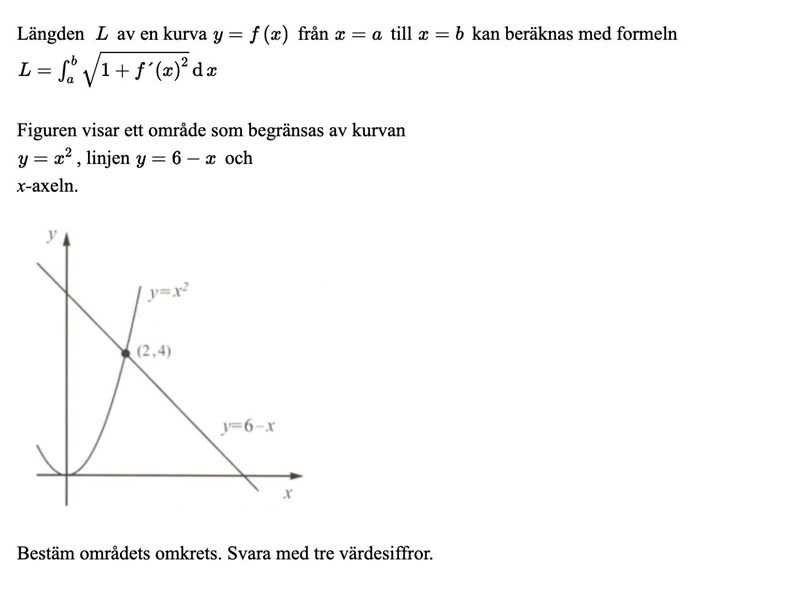
Hej! jag har länge försökt lösa uppgiften men kommer ingen vart, kan man få typ en ledtråd?
T ex du har y=f(x)=x^2. Utnyttja formeln på L för att räkna längden på 2:a grads funktionen.
Det är omkretsen du skall beräkna.

Längden av de två "röda" linjerna i bifogad figur är lätta att bestämma.
Längden av parabelbågen: Där måste du använda integralformeln, enligt rapidos replik.
Summa av alla tre längderna utgör svaret.
jag har använt formel L för andra grads funktionen men jag fick lösningen 38/3, när jag ska addera alla mina lösningar dvs 38/3 + roten ur 8 + 6 =21,50 vilket inte stämmer med facit. Vad har jag gjort för fel?
Fel område?
Enl texten begränsas det av x-axeln...
men när jag försöker lösa andra området så får jag 6+roten ur 57+ (38/3) = 26,22 vilket stämmer inte heller med facit
Visa dina räkningar, så får vi se var det kan ha gått snett.
Den krökta linjen ser inte ut att vara dubbelt så lång som "basen" 6.
Hur fick du roten ur 57 ?
Detta kanske hjälper, det borde se ut nåt liknande såhär?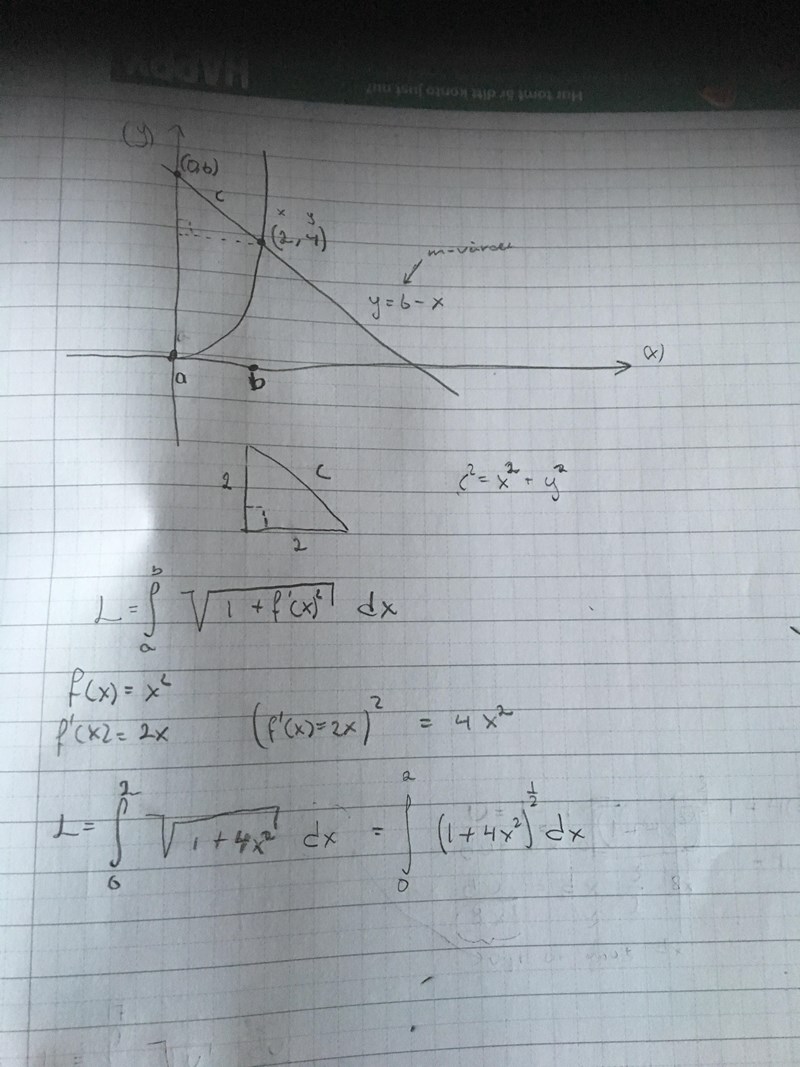
Vad ska svaret vara säger facit ?
Jo, fel av mig. Läste slarvigt och förväxlade x och y-axel. Ursäkta.
Kan man verkligen lösa den här integralen med enbart gymnasiekunskaper?
Varifrån kommer uppgiften?
Frågan du ställer, Arktos, är relevant. Uppgiften känns mer baskurs hing.
Jag vet inte vad kurvlängden blir, men 38/3 är för mycket. Det är ungefär 13 och det är mer än kateterna i triangeln tillsammans.
svaret enligt fact är 16,31
Liddas skrev:Detta kanske hjälper, det borde se ut nåt liknande såhär?
Jag löste med precis samma metod men det stämmer inte med facit..
Arktos skrev:Kan man verkligen lösa den här integralen med enbart gymnasiekunskaper?
Varifrån kommer uppgiften?
uppgiften har vi fått via kunskapsmatrisen
Jag tror att tanken är att lösa integralen numeriskt, att man skriver om ”tre värdesiffror” i frågan indikerar det också.
Vet du hur man räknar ut en integral numeriskt på din grafräknare alternativt via nätet?
Det ska inte bli 16,13 ?
nej, har inte använt det på med det på länge så har glömt bort
Ska svaret inte bli 16,13? Du skrev 16,31 ?
Jag får svaret till 16,13 iaf, kan va fel, men mitt första lösningsförslag visar omkretsen som begränsas mot y-axeln och när jag läser uppgiften igen är det ju faktiskt fel område, det är ju kurvan L =x^2 linjen y=6-x och x-axeln som omkretsen gäller! Nån fler som tolkar det som jag?
Det ska vara mot x-axeln, alltså följande linjesegment:
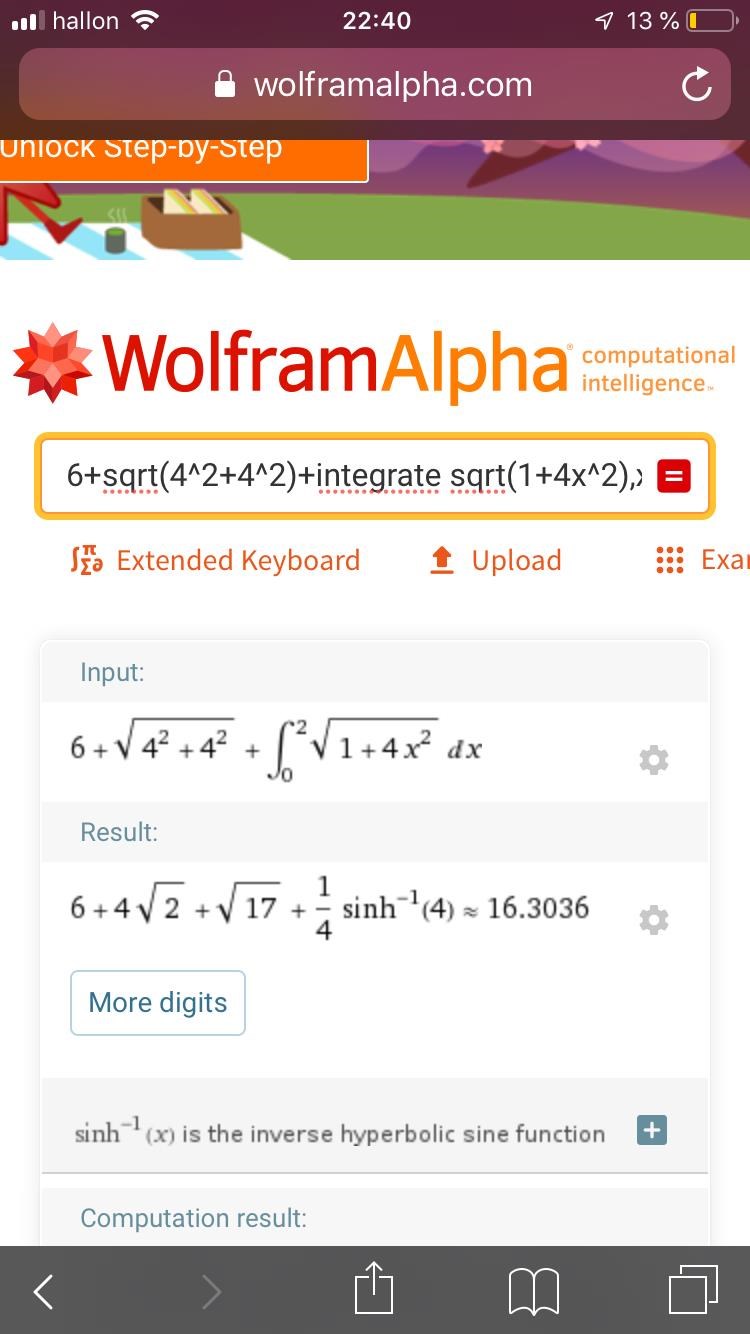
Liddas skrev:Jag får svaret till 16,13 iaf, kan va fel, men mitt första lösningsförslag visar omkretsen som begränsas mot y-axeln och när jag läser uppgiften igen är det ju faktiskt fel område, det är ju kurvan L =x^2 linjen y=6-x och x-axeln som omkretsen gäller! Nån fler som tolkar det som jag?
Jag tolkar som du. Jag räknade kurvan med en grov linjärapproximation och avståndsformeln och fick 16,15 total omkrets. Storleksordningen borde vara rätt.





