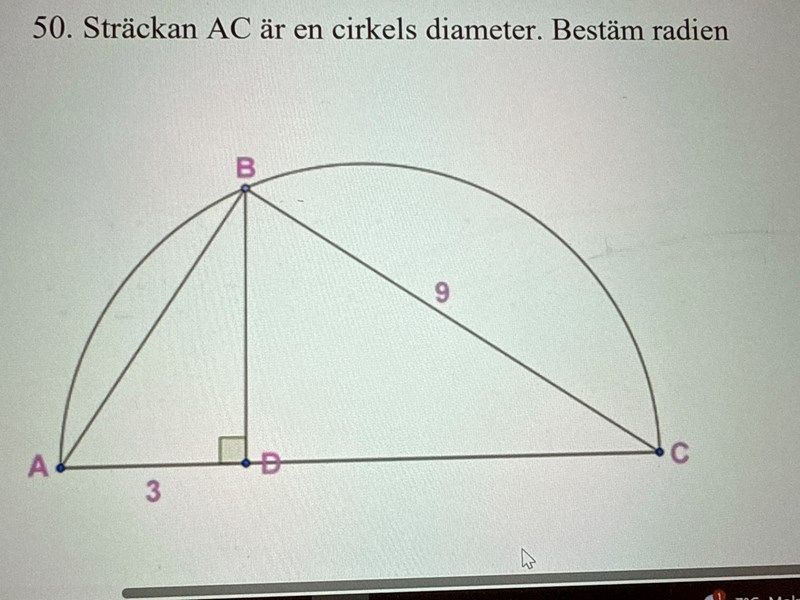
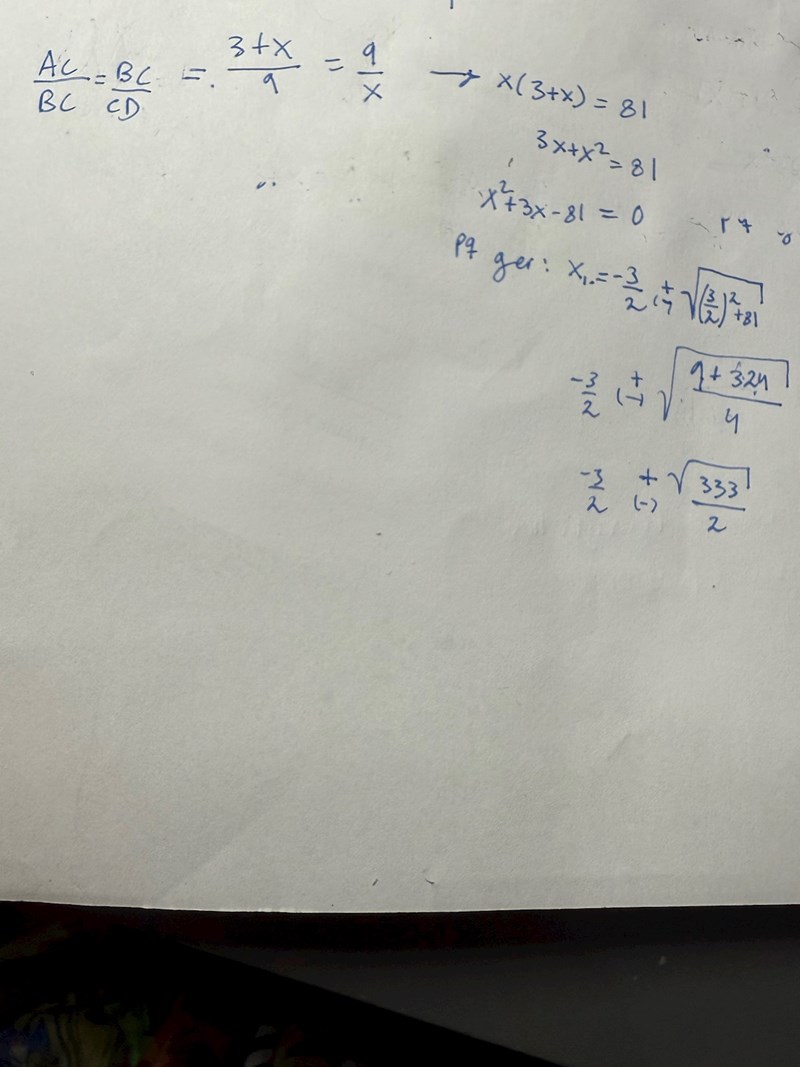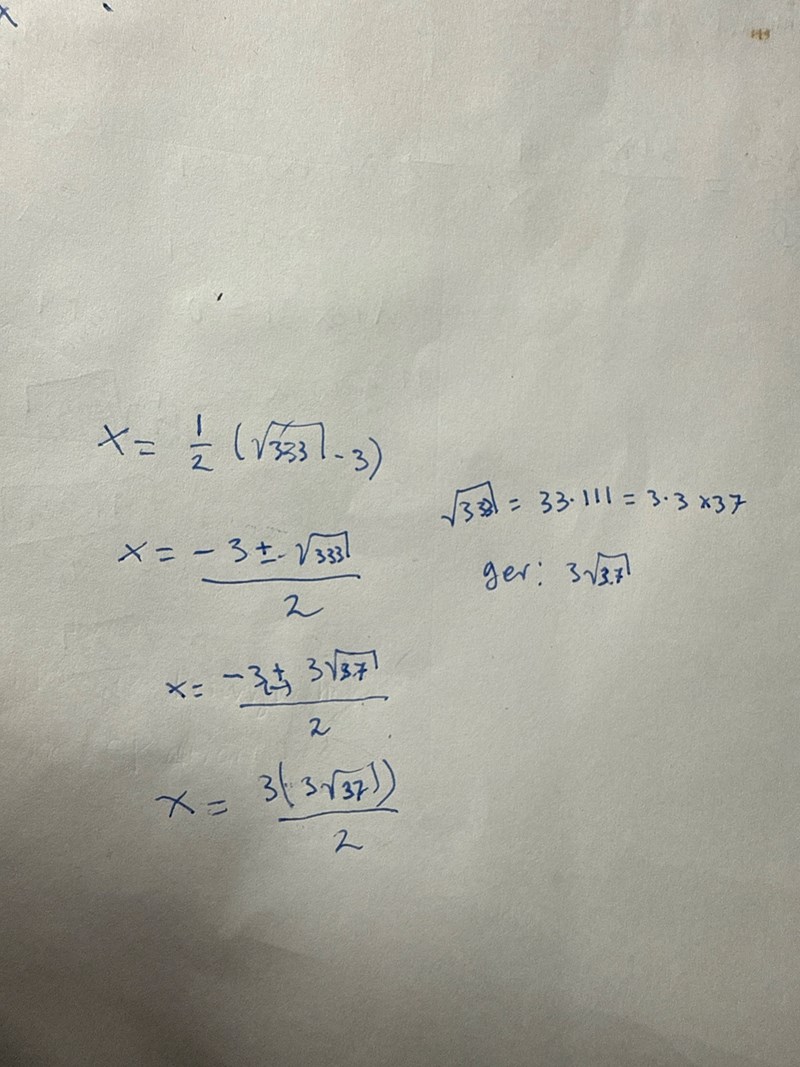Beräkna radien

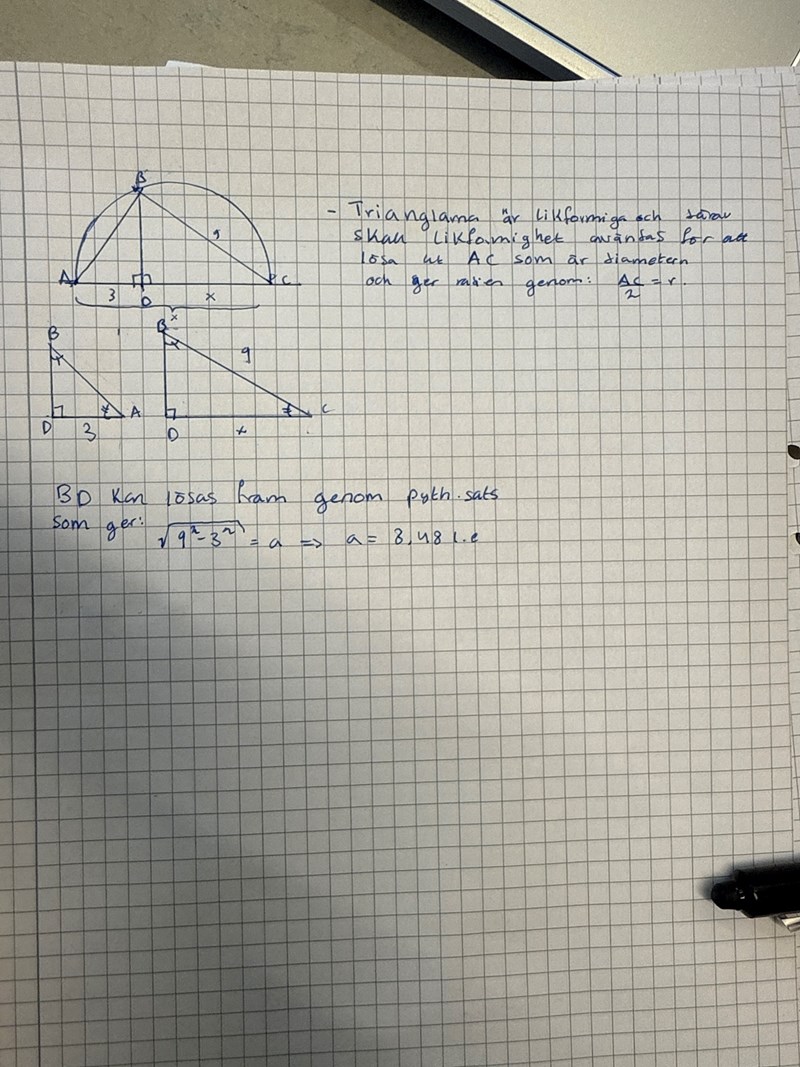
Det är nog så att även ABC är rätvinklig. Jag har glömt vad det kallas. 

Vad syftar du på exakt? Ska jag räkna ut med Pythagoras sats? 

Om det kan bevisas att ABC är rätvinklig är den likformig med ADB. 

Pieter Kuiper skrev:

Om det kan bevisas att ABC är rätvinklig är den likformig med ADB. 

Drt går att visa med hjälp av randvinkelsatsen.

ja exakt medelpunktsvinkeln = 180 grader då det är en rät linje som går igenom medelpunktsvinkeln.

Vilket ger 180-90 grader= 90 grader alltså är den rätvinklig. 

Därav kan man använda likformighet men jag vet inte riktigt hur ekvationerna blir. 

Jag har även löst ut ena kateten via pyth sats men vet inte om det är relevant?

Hur tänker du i #1 när du sätter in hypotenusan i en triangel och en katet i en annan triangel i Pythagoras sats?

tänkte på likformighet men vet inte hur jag skall gå tillväga 

Men du är med på att beräkningen av BD i #1 inte stämmer?
Bara ett inpass, jag ska inte ta över tråden.

 okeejj jag tar bort mina första beräkningar men...  Vad menas kommer du inte hjälpa mig längre ?

Jag menar att eftersom Pieter började hjälpa dig ska jag inte tränga mig in.
Ifall han vill fortsätta.

Skulle du kunna fortsätta tack

Anika1 skrev:

Skulle du kunna fortsätta tack

Jag tycker bara att du borde kunna fortsätta själv lite.

Ett tips som jag gav dig tidigare är att markera korresponderande sidor med färg: https://www.pluggakuten.se/trad/berakna-okanda-stackor-genom-likformighet/?order=all#post-c5a08d38-c0a7-43de-9f59-b2c400ad3cb1 

Jag förstår ditt tankesätt och det borde vara så men jag hatar verkligen likformighet för att jag lyckas aldrig med att få rätt på ekvationerna, jag har gått igenom flera genomgångar och gjort många uppgifter men ändå så blir det fel! 

Men jag kan testa igen, men skulle jag kunna få typ en ledtråd så att jag kan beräkna vidare.

Anika1 skrev:

[...]

Men jag kan testa igen, men skulle jag kunna få typ en ledtråd så att jag kan beräkna vidare.

Du har tre likformiga trianglar i figuren, nämligen ABC, ABD och BCD.

Som tur är så är alla rätvinkliga, vilket gör det lättare att se vilka sidor som hänger ihop med vilka.

Hypotenusorna hänger ihop med varandra, de korta kateterna hänger ihop med varandra och de långa kateterna hänger ihop med varandra.

I triangeln ABC så är hypotenusan AC, den korta kateten AB och den långa kateten BC.

Kan du själv hitta hypotenusan, den korta ich dennlånga kateten i ABD och BCD?

Gör gärna en tabell vid sidan av så slipper du hålla så mycket i huvudet på en gång.

Det behöver inte vara snyggt, det här duger utmärkt:

Okkeeyy tackar jag ska ge det ett försök

Det blir väldigt tomt på de flesta ställen…

så här har jag gjort 

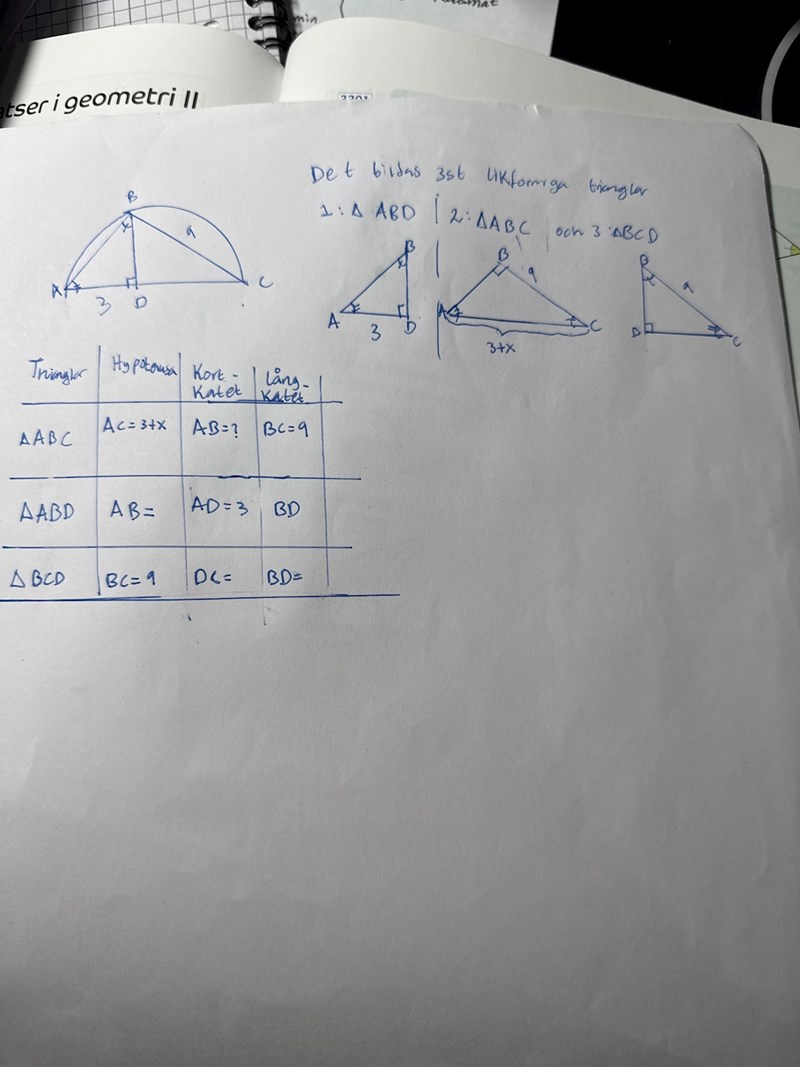
Långkateten kan inte vara lika (BD) för likformiga trianglar som är olika stora. 

så här nu har jag gjort om stämmer det nu?

Testade även en grej för att försöka sj men är helt ute och cyklar 🤦🏽‍♀️

Pieter Kuiper skrev:

Långkateten kan inte vara lika (BD) för likformiga trianglar som är olika stora. 

Okej tack! 

ger likformighet detta : 3+x/9 = 3/9 

eller 3+x/x = 9/9? 

Anika1 skrev:

[...]

så här nu har jag gjort om stämmer det nu?

Ja, Den här tabellen stämmer bra:

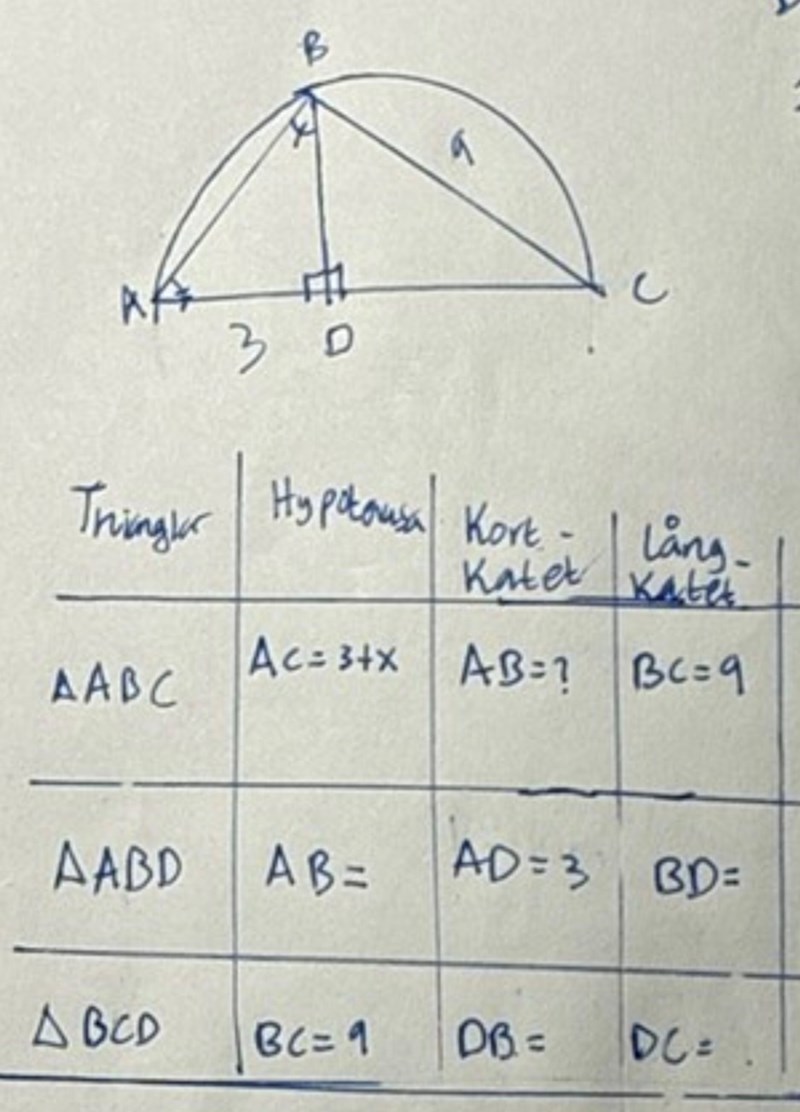
Anika1 skrev:

[...] 

ger likformighet detta : 3+x/9 = 3/9 

 

eller 3+x/x = 9/9? 

Med hjälp av tabellen kan du ställa upp ett flertal olika likformighetssamband som alla gäller.

Eftersom det som eftersöks är radien, dvs halva längden av hypotenusan i ABC så kan det vara lämpligt att välja ett samband där längden av denna hypotenusa ingår.

Exempelvis  "längden av hypotenusan i ABC"/"längden av hypotenusan i BCD" = "längden av långa kateten i ABC"/"längden av långa kateten I BCD", dvs |AC|/|BC| = |BC|/|CD|

Kommer du vidare då?

Men jag vet ej vad  CD är 

Anika1 skrev:

Men jag vet ej vad BC och  CD är 

Du vet vad längden av BC är.

Längden av CD har du väl kallat x?

Jag vet BC råkade skriva fel syftade på CD kan man sätta den som x ? Det visste jag inte isåfall är ju detta inte så svårt 

Anika1 skrev:

Jag vet BC råkade skriva fel syftade på CD kan man sätta den som x ?

Ja det kan du göra. Jag trodde att du redan hade gjort det iom detta:

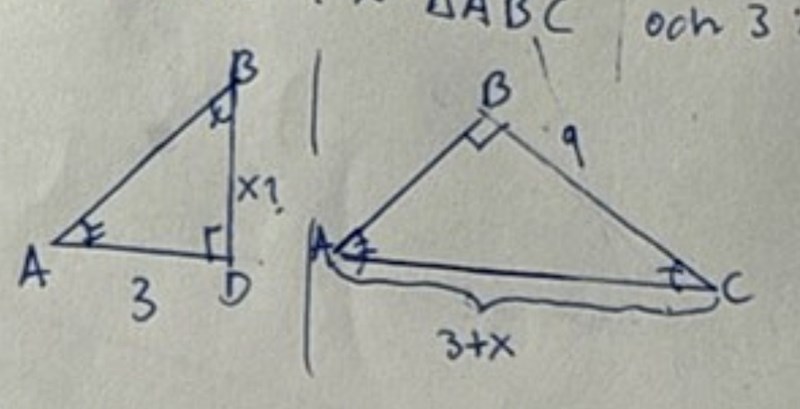
Det visste jag inte isåfall är ju detta inte så svårt 

Nej, det är oftast inte så svårt om man går systematiskt tillväga.

(Men du behöver egentligen inte göra hela tabellen för alla tre trianglarna, jag visade det mest för att skapa förståelse för hur man kan strukturera den information man kan få ut av uppgiften.)

Men jag för att lösa x blir det pq och det är udda tal det kan ju inte stämma

Du har att

• |AC| = 3+x
• |BC| = 9
• |CD| = x

Sätt in detta i likformighetssambandet och försök att lösa ut x. Visa alla steg I dina uträkningar.

OK, du har alltså att $x=\frac{1}{2}(\sqrt{333}-3)$

Du kan förenkla detta uttryck genom att faktorisera talet 333.

Vad blir då radien?

1/2 tar det bort rotteckenet? 

Visa dina uträkningar så spar vi tid.

Anika1 skrev:

1/2 tar det bort rotteckenet? 

Nej.

Börja med att faktorisera talet 333 så långt det går.

Det stämmer att $\sqrt{333}=\sqrt{9\cdot37}=3\sqrt{37}$

Men sen förstår jag inte riktigt vad du gör.

Så här ska det vara:

$x=\frac{1}{2}(\sqrt{333}-3)=$

$=\frac{1}{2}(3\sqrt{37}-3)=$

$=\frac{3}{2}(\sqrt{37}-1)$

Du vet att cirkelns diameter är |AC| = 3+x.

Då blir cirkelns radie hälften av detta.

Yngve skrev:

Det stämmer att $\sqrt{333}=\sqrt{9\cdot37}=3\sqrt{37}$

Men sen förstår jag inte riktigt vad du gör.

Så här ska det vara:

$x=\frac{1}{2}(\sqrt{333}-3)=$

$=\frac{1}{2}(3\sqrt{37}-3)=$

$=\frac{3}{2}(\sqrt{37}-1)$

Du vet att cirkelns diameter är |AC| = 3+x.

Du blir cirkelns radie hälften av detta.

Förlåt men jag fattar ingenting, ska jag sammanställa alltså 3+x = =32(37-1)

Anika1 skrev:

Förlåt men jag fattar ingenting, ska jag sammanställa alltså 3+x = =32(37-1)

Nej, du har bestämt x, dvs längden av sträckan DC.

Är du med på att cirkelns diameter är 3+x?

Eftersom trianglarna ABC och BDC är likformiga ( 1. båda rätvinkliga och 2. de har vinkeln C gemensam ) kan vi skapa förhållandena :

BC/AC = CD/BC = BD/AB

Genom korsmultiplikation mellan de första två, får du att BC^2 = AC * CD där AC är 2r , CD= 2r-3 och BC^2 = 81

En 2a gradsekvation med okänd variabeln r.

Skulle du kunna lösa det snälla har hållit på med detta för länge! 

Anika1 skrev:

Skulle du kunna lösa det snälla har hållit på med detta för länge! 

Nej du är ju nästan framme. Vi gör det tillsammans.

Är du med på att cirkelns diameter är 3+x?

Yngve skrev:

Anika1 skrev:

Skulle du kunna lösa det snälla har hållit på med detta för länge! 

Nej vi gör det tillsammans.

Är du med på att cirkelns diameter är 3+x?

yes!! 🫡

Bra.

Är du med på att cirkelns radie då är (3+x)/2?

Yngve skrev:

Bra.

Är du med på att cirkelns radie då är (3+x)/2?

Jajamensan!

Bra.

Du vet att $x=\frac{3}{2}(\sqrt{37}-1)$.

Kan du då skriva ett uttryck för radien?

Skriv för hand och ladda upp en bild.

Ja sammanställning 3+x/2 = det pq och favoriseringen gav 

Nej det är enklare än så.

Radien är $\frac{3+x}{2}$ och $x=\frac{3}{2}(\sqrt{37}-1)$

Det ger dig att radien är lika med $\frac{3+\frac{3}{2}(\sqrt{37}-1)}{2}$

Detta uttryck kan förenklas.

Detta är min lösning: 

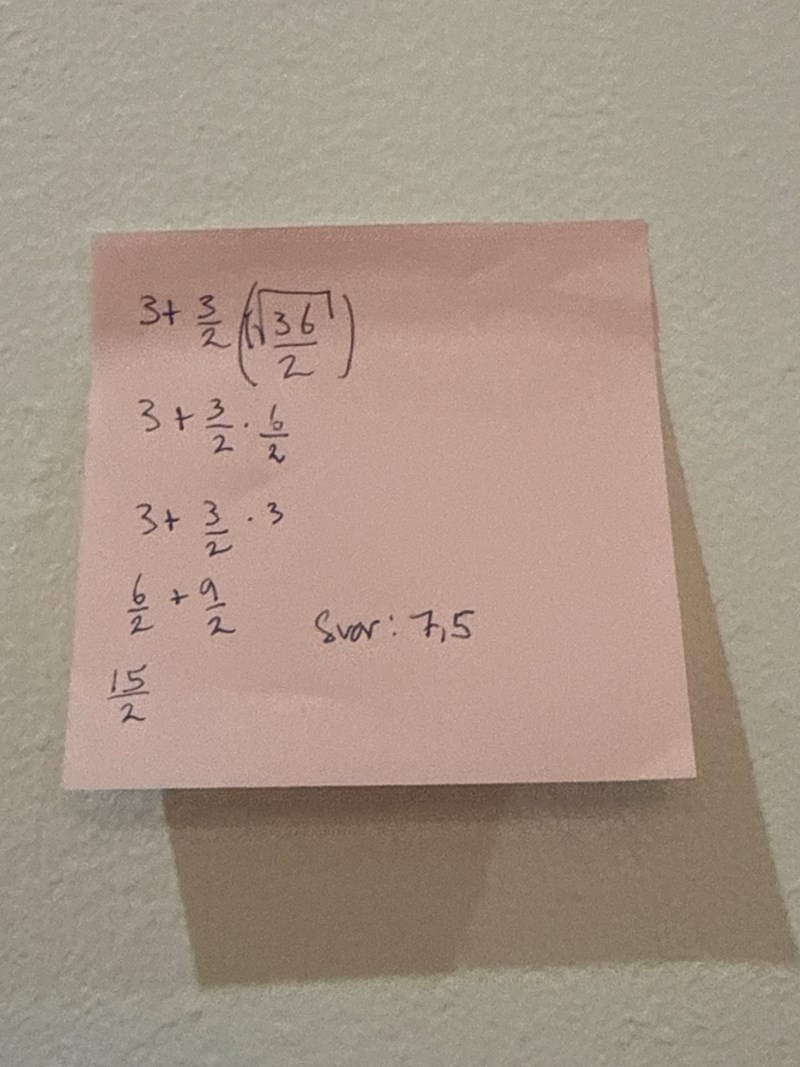
Anika1 skrev:

 

Detta är min lösning: 

 

Något är fel. Blir ca 5.3. Se #46

Anika1 skrev:

Detta är min lösning: 

[...]

Du skriver av uttrycket fel.

Det står $\sqrt{37}-1$, inte $\sqrt{37-1}$.

Dessutom hamnar tvåan i nämnaren fel.

Så här ska det vara:

$\frac{3+\frac{3}{2}(\sqrt{37}-1)}{2}=$ 

(Förläng täljarens ensamma trea med två)

$=\frac{\frac{2\cdot3}{2}+\frac{3}{2}(\sqrt{37}-1)}{2}=$

(Skriv täljaren på gemensamt bråkstreck)

$=\frac{\frac{6+3(\sqrt{37}-1)}{2}}{2}=$

(Använd att $\frac{\frac{a}{b}}{\frac{c}{d}}=\frac{a}{b}\cdot\frac{d}{c}$)

$=\frac{6+3(\sqrt{37}-1)}{4}=$

(Multiplicera in trean i parentesen i täljaren)

$=\frac{6+3\sqrt{37}-3}{4}=$

(Förenkla täljaren)

$=\frac{3+3\sqrt{37}}{4}=$

(Bryt ut faktorn tre i täljaren)

$=\frac{3(1+\sqrt{37})}{4}=$

(Skriv om)

$=\frac{3}{4}(1+\sqrt{37})$

--------------------

Rimlighetskontroll: $\frac{3}{4}(1+\sqrt{37})\approx5,3$

Det verkar rimligt att radien är ungefär 5 l.e.

Ojdå tack så jättemycket för all hjälp! Uppskattar det enormt!!

Varsågod, men hängde du med på alla steg?

Yngve skrev:

Varsågod, men hängde du med på alla steg?

yes!! Du förklarade enormt bra och hjälpte även mig, nu vet jag hur man kan tänka vid likformighet vilket är genom att göra en enkel tabell som gör allt såååå mycket tydligare!!

Bra!

Jag tror stenhårt på alla metoder som minskar behovet av att hålla reda på flera saker I huvudet samtidigt.