Beräkna sannolikheten att hon träffar A3 med sitt sjätte skott
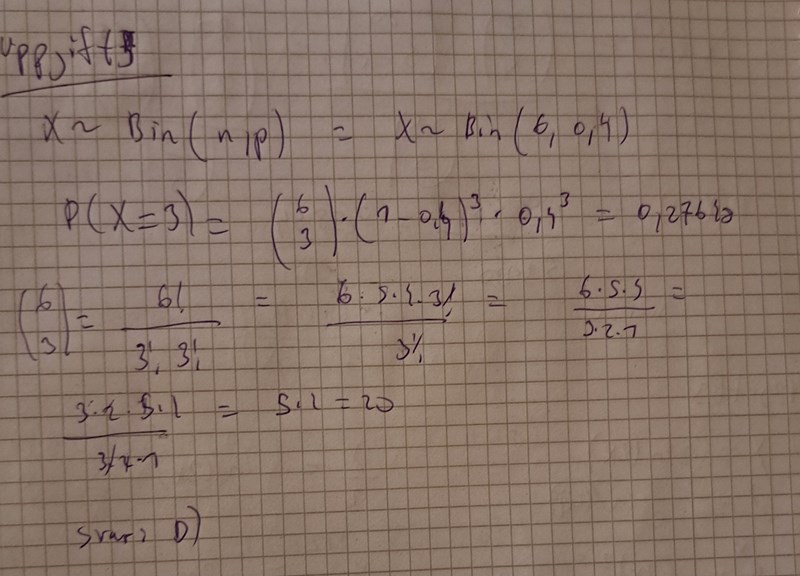
Hej!
Rätt svar är B) och inte D) vilket jag inte förstår varför det är så. Jag räknade antalet skott n är 6 st.
Nu är jag inte bekant med den matematik du använder, men behöver man göra det så krångligt? Man kan ju få B) genom att bara multiplicera sannolikheterna för tre missar och tre träffar =)
thedifference skrev:Nu är jag inte bekant med den matematik du använder, men behöver man göra det så krångligt? Man kan ju få B) genom att bara multiplicera sannolikheterna för tre missar och tre träffar =)
och multiplicera med antalet sätt att få det resultatet.
thedifference skrev:Nu är jag inte bekant med den matematik du använder, men behöver man göra det så krångligt? Man kan ju få B) genom att bara multiplicera sannolikheterna för tre missar och tre träffar =)
Hur får man 3 missar och 3 träffar? Jag hänger tyvärr inte med. Jag tänkte det har med binomialfördelning att göra.
För att kunna träffa A3 måste du redan ha träffat två gånger, för att ha tagit dig till A3. Träffen på A3 blir din tredje träff. För att det ska vara sjätte skottet så måste du ha missat tre gånger.
Men jag kan inte säga mer än så, jag bara uppmärksammade att det gick att komma fram till det svaret utan krångligare resonemang. Kanske bara är en slump =)
thedifference skrev:För att kunna träffa A3 måste du redan ha träffat två gånger, för att ha tagit dig till A3. Träffen på A3 blir din tredje träff. För att det ska vara sjätte skottet så måste du ha missat tre gånger.
Men jag kan inte säga mer än så, jag bara uppmärksammade att det gick att komma fram till det svaret utan krångligare resonemang. Kanske bara är en slump =)
Jag bifogar lösningsförslaget iom att jag har några frågor gällande hur de gjorde.

1) vad innebär att det är två träffar och 3 missar i förhållande till A3, A4 ,A5 och A6?
2) varför använder de sig av Bin(5,0.4) och px(2) och inte Bin(6,0.4) med px(3) som jag var inne på?
3) Till slut multiplicerar de sannolikhet svaret från px(2) med 0.4. Varför gör de det?
Tre missar och tre träffar funkar inte, vi har att det sjätte skottet specifikt ska vara en träff.
Så vi har att vi först ska träffa två av fem och sedan det sjätte.
(5 över 2)*0,4^2*0,6^3*0,4=13,824%.
I ditt ursprungliga svar har du beräknat att personen får tre träffar på sex skott, inte att det sjätte skottet är den tredje träffen.
Du har alltså räknat sannolikheten att hon skjutit 6 skott och träffat 3. Ett scenario där det sker är att hon träffar sina 3 första skott och sedan missar 3 skott när hon försöker skjuta på . Men det var ju inte vad frågan frågade efter. I frågan vill man veta att specifikt det sjätte skottet träffade målet .
Alltså, bland det 5 första skotten ska hon träffat 2 (det är en binomialfördelning) och sedan på det sjätte skottet träffa målet. P(träffa 2 skott av 5)*P(träffa sjätte skottet)
Hondel skrev:Du har alltså räknat sannolikheten att hon skjutit 6 skott och träffat 3. Ett scenario där det sker är att hon träffar sina 3 första skott och sedan missar 3 skott när hon försöker skjuta på . Men det var ju inte vad frågan frågade efter. I frågan vill man veta att specifikt det sjätte skottet träffade målet .
Alltså, bland det 5 första skotten ska hon träffat 2 (det är en binomialfördelning) och sedan på det sjätte skottet träffa målet. P(träffa 2 skott av 5)*P(träffa sjätte skottet)
Men hur kan vi ha 5 skott när uppgiften gav oss 6 skott? Du menar att hon måste träffa A1 och A2 först 2 gånger och sen inte träffa A4, A5 och A6 och sen träffa bara A3?
Varför multiplicerar man sannolikheterna? Vad blir P(träffa sjätteskott) i binomialfördelning)?
destiny99 skrev:Men hur kan vi ha 5 skott när uppgiften gav oss 6 skott? Du menar att hon måste träffa A1 och A2 först 2 gånger och sen inte träffa A4, A5 och A6 och sen träffa bara A3?
Varför multiplicerar man sannolikheterna? Vad blir P(träffa sjätteskott) i binomialfördelning)?
Man får inte skjuta mot A4, A5 eller A6 innan man träffat A3.
En godtagbar serie är att man skjuter två skott mot A1 och träffar med andra skottet. Sedan skjuter man två gånger mot A2 och träffar med fjärde skottet. Slutligen skjuter man två gånger mot A3 och träffar med sjätte skottet.
En annan godtagbar exempelserie är att man skjuter 3 skott mot A1 och träffar med tredje skottet. Sedan skjuter man två skott mot A2 och träffar med femte skottet. Slutligen skjuter man ett skott mot A3 och träffar med sjätte skottet (första försöket på A3).
D4NIEL skrev:destiny99 skrev:Men hur kan vi ha 5 skott när uppgiften gav oss 6 skott? Du menar att hon måste träffa A1 och A2 först 2 gånger och sen inte träffa A4, A5 och A6 och sen träffa bara A3?
Varför multiplicerar man sannolikheterna? Vad blir P(träffa sjätteskott) i binomialfördelning)?
Man får inte skjuta mot A4, A5 eller A6 innan man träffat A3.
En godtagbar serie är att man skjuter två skott mot A1 och träffar med andra skottet. Sedan skjuter man två gånger mot A2 och träffar med fjärde skottet. Slutligen skjuter man två gånger mot A3 och träffar med sjätte skottet.
En annan godtagbar exempelserie är att man skjuter 3 skott mot A1 och träffar med tredje skottet. Sedan skjuter man två skott mot A2 och träffar med femte skottet. Slutligen skjuter man ett skott mot A3 och träffar med sjätte skottet (första försöket på A3).
Ja okej. Men var kommer 5 skott ifrån? Man skjuter alltså 2 skott på A1 och A2 dvs man kan skjuta 3 skott på A1 och få en träff på tredje skott och sen skjuta 2 skott på A2 och få en träff på femte skott. Då har man totalt skjutit 5 skott eller? Jag förstår att det sjätte skottet ska träffa A3 och då får man en träff. Men kan man då inte ställa upp en binomialfördelning för skottet för A1 och A2 så att vi har 5 över 3 och sen 5 över 2 där 3 är antal skott mot A1 och 2 är antal skott mot A2 ?
Hon skjuter 6 skott, det sjätte skottet vet vi är en träff, så det återstår 5 skott som vi inte vet om de är träff eller miss.
Av de fem skotten vet vi att två är träff, den första en träff på A1, den andra en träff på A2. 5 över 2 möjligheter för vilka av de 5 som är träffar.
Smutsmunnen skrev:Hon skjuter 6 skott, det sjätte skottet vet vi är en träff, så det återstår 5 skott som vi inte vet om de är träff eller miss.
Av de fem skotten vet vi att två är träff, den första en träff på A1, den andra en träff på A2. 5 över 2 möjligheter för vilka av de 5 som är träffar.
Yes nu är jag med. Då söker vi P(X=2 av 5 skott )=(5 2)*0.4^2*(1-0.4)^3. Men varför multiplicerar vi sen med 0.4 ?
Därför att det sjätte skottet ska vara en träff för vilket sannolikheten är 0,4.
Vi har alltså två olika, oberoende händelser som ska inträffa.
Den första är exakt två träffar på de första 5 skotten. Sannolikhet enligt binomialfördelningen.
Den andra att skott 6 är en träff, sannolikhet 0,4.
Smutsmunnen skrev:Därför att det sjätte skottet ska vara en träff för vilket sannolikheten är 0,4.
Vi har alltså två olika, oberoende händelser som ska inträffa.
Den första är exakt två träffar på de första 5 skotten. Sannolikhet enligt binomialfördelningen.
Den andra att skott 6 är en träff, sannolikhet 0,4.
Aa okej så man söker P(AsnittB)=P(A)*P(B) dvs sannolikheten A och B inträffar ?
Jag räknade på det här viset:
Det blir tre träffar och därmed tre missar, och sannolikheten för en viss sådan serie är 0,43 0,63 = 0,0138, som någon redan räknade ut längre upp.
Antalet olika sådan serier är hur många sätt det finns att missa (för att träffa har man inget val, man träffar en gång per mål). Man ska alltså bilda summan 3 (antalet missar) av tre heltal (0, 1, 2 eller 3).
Det finns säkert nåt fiffigt sätt att räkna ut det, men jag skrev bara upp alla sätten, 003, 012, 021 osv. och det är tio stycken.
10 gånger 0,0138 är 0,138.


