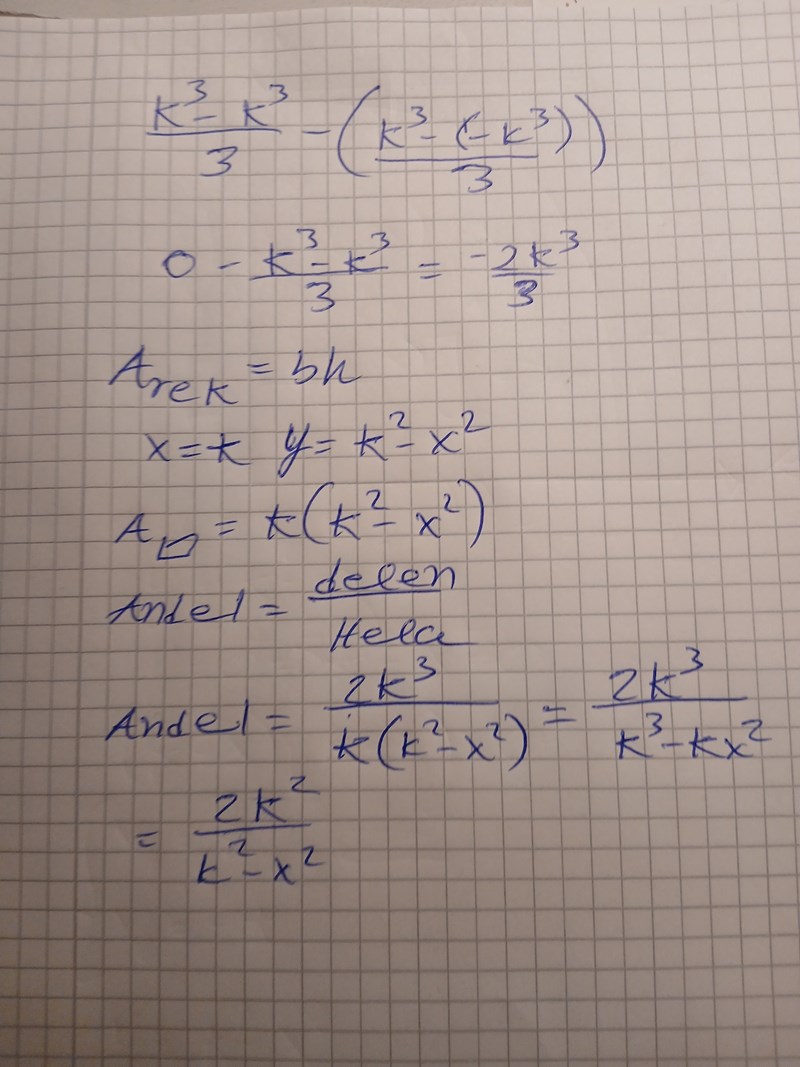Beräkna skuggade andelen mha integraler

Så här har jag tänkt

Frågan är on jag har integrerat $k$fel 

borde det inte vara så här ?

$\int \left(k^2\right)dx=k^{2}x$

Arup skrev:

Så här har jag tänkt

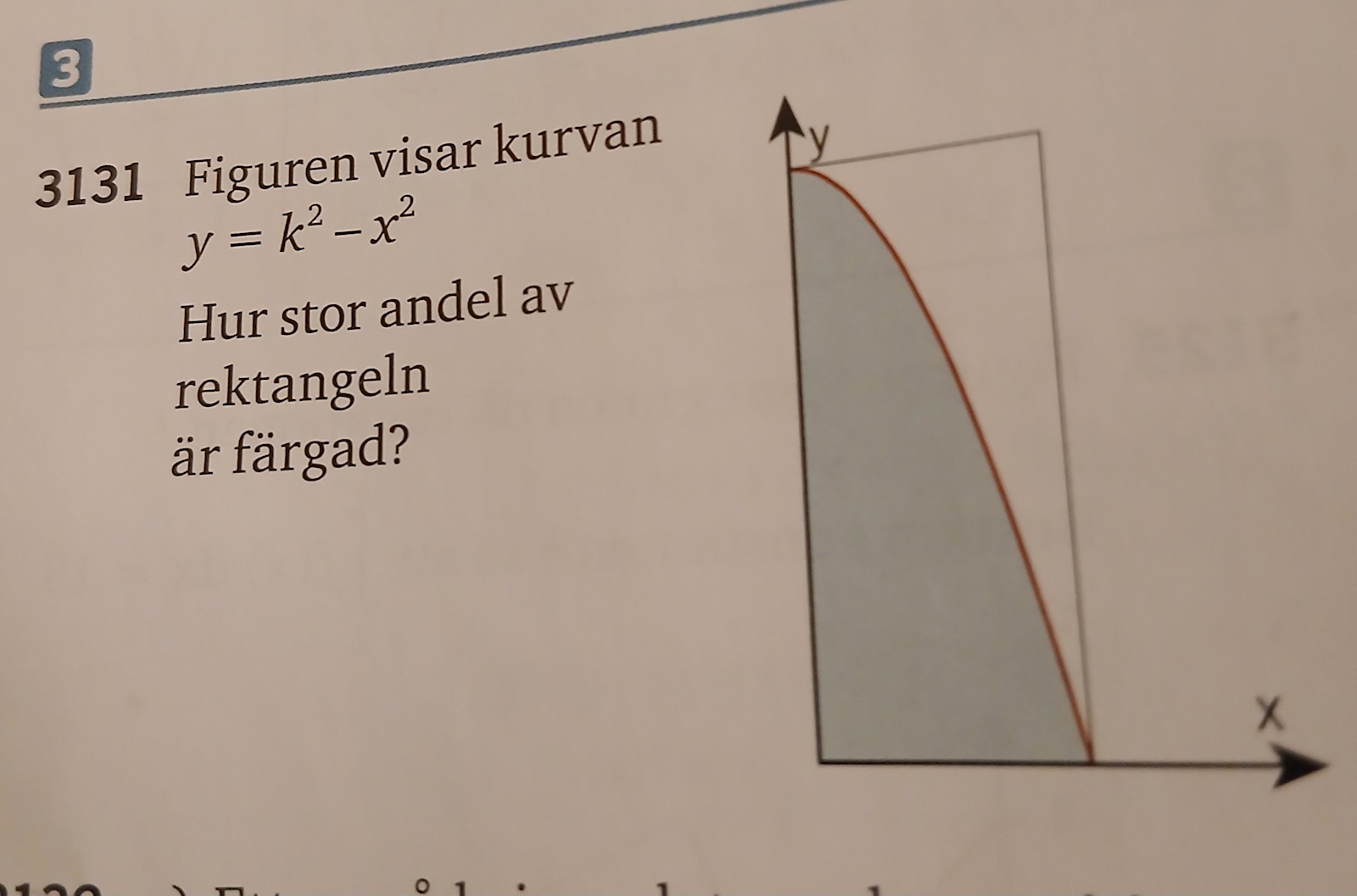
Varför integrerar du från -k. Ur bilden får vi att vänstra gränsen är x=0.

Sedan är prim.fkn fel.

I funktionen är k² en konstant. Vad händer med den när du integrerar med avseende på x?

sictransit skrev:

I funktionen är k² en konstant. Vad händer med den när du integrerar med avseende på x?

$k^{2}x ?$

Arup skrev:

sictransit skrev:

I funktionen är k² en konstant. Vad händer med den när du integrerar med avseende på x?

$k^{2}x ?$

Stämmer bra!

jag ser inte var i bilden den vänstra gränsen är där $x=0 ?$

Arup skrev:

jag ser inte var i bilden den vänstra gränsen är där $x=0 ?$

Vänstra gränsen är y-axeln, alltså x=0. 

ok, så om jag stoppar in $x=0$

i funktionen $y=k^2-x^2$

får jag:

$$\begin{gathered} y=k^2-0^2 \\ y=k^2 \end{gathered}$$

Hur hjälper det här mig ?

Ja, du behöver ju också räkna ut rektangelns area. Nu har du höjden på den. 

ok, så för att räkna ut rektangelns area behlver vi 

både basen$\times$höjden

enligt funktionen har vi: 

$y=k^2-x^2$, vilket kan skrivas om genom genom konjugat regeln

$y=(k+x)(k-x)$

Vi kan få dess bas/ bredd när y=0, för då får vi funktionen nollställen/ rötter

$$\begin{gathered} (k+x)(k-x)=0 \\ {x}_1=k \\ \left(x_2=-k\right) \end{gathered}$$

Precis! Basen är k (och där har du även din övre integrationsgräns), höjden är k².

ok,  då tror jag förstår. Jag undrar vad är min undre integrations gräns ?

Arup skrev:

ok,  då tror jag förstår. Jag undrar vad är min undre integrations gräns ?

Läs mitt svar #10. 

sictransit skrev:

Arup skrev:

jag ser inte var i bilden den vänstra gränsen är där $x=0 ?$

Vänstra gränsen är y-axeln, alltså x=0. 

Ok, men i #13 fick $x=\pm k$

så är min undre gräns då $-k ?$

Arup skrev:

sictransit skrev:

Visa föregående citat

Arup skrev:

jag ser inte var i bilden den vänstra gränsen är där $x=0 ?$

Vänstra gränsen är y-axeln, alltså x=0. 

Ok, men i #13 fick $x=\pm k$

så är min undre gräns då $-k ?$

Om du sätter y=0 är x=-k en lösning. Det stämmer.

Du måste dock titta på grafen i uppgiften.

Ser du att kurvan och rektangeln vars areor du skall beräkna börjar vid y-axeln, alltså då x=0?

så är den övre gränsen $k^{2 ?}$

Jag testar igen

Arup skrev:

så är den övre gränsen $k^{2 ?}$

Nej, se tidigare svar. Den övre är k. Nu ser jag att du ändå räknat rätt. 

nej, det är ju $k^2$

för att ekvationen är 

$y=k^2-x^2$

Hur resonerar du då?

Du har ju använt k som integrationsgräns.

Dessutom får du x=k som en lösning när y=0.

Det går även att se i grafen att basen är väsentligt kortare än höjden, den som du konstaterat är k².