Beräkna Thevinin Ekvivalent

Jag vill beräkna Thévenin ekvivalenten till kretsen på bilden ovan. Jag har påbörjat min lösning på följande sätt:
(1) Bestäm RTH
För att hitta RTH Kan vi betrakta kretsen när alla oberoende ström- och spänningskällor har nollställs. I detta fall kan vi "koppla bort" strömkällorna och betrakta en ny krets med bara R2 och R3 som då är seriekopplade. Alltså får jag RTH = (R2 + R3).
Sedan känner jag mig inte helt säker på hur jag bör gå tillväga för att bestämma VTH . I samtliga exempel jag har läst så finns ytterligare en spänningskälla och att man då "ser" man att spänningen är ekvivalent med spänningen över det element som sitter parallellt med AB.
Då jag saknar facit eller lösningsförslag är jag osäker på hur jag bör gå fortsätta med denna uppgift. Alla tips uppskattas!
wedan skrev:det element som sitter parallellt med AB.
Det är alltså R2.
Ja - men varför? Borde inte spänningen över AB vara densamma som spänningen över (R2 + R3) isåfall?
wedan skrev:Ja - men varför? Borde inte spänningen över AB vara densamma som spänningen över (R2 + R3) isåfall?
Vid öppen krets går det ingen ström genom R3, spänningsfallet över den är noll, VAB = VR2.
Tack - jag hittade en liknande uppgift med lösningsförslag så tror jag fått lite mer klarhet och förstår varför det blir som du säger. Om man betraktar den ursprungliga kretsen och jordar en av noderna längst ned så ser man att potentialen över IB = V1 = VTH . Eftersom det är en direkt koppling längst upp mellan V1 och V2 (markerat i figuren nedan) så gäller då även att V2 = VTH alltså att potentialen över R2 är ekvivalent med VTH .
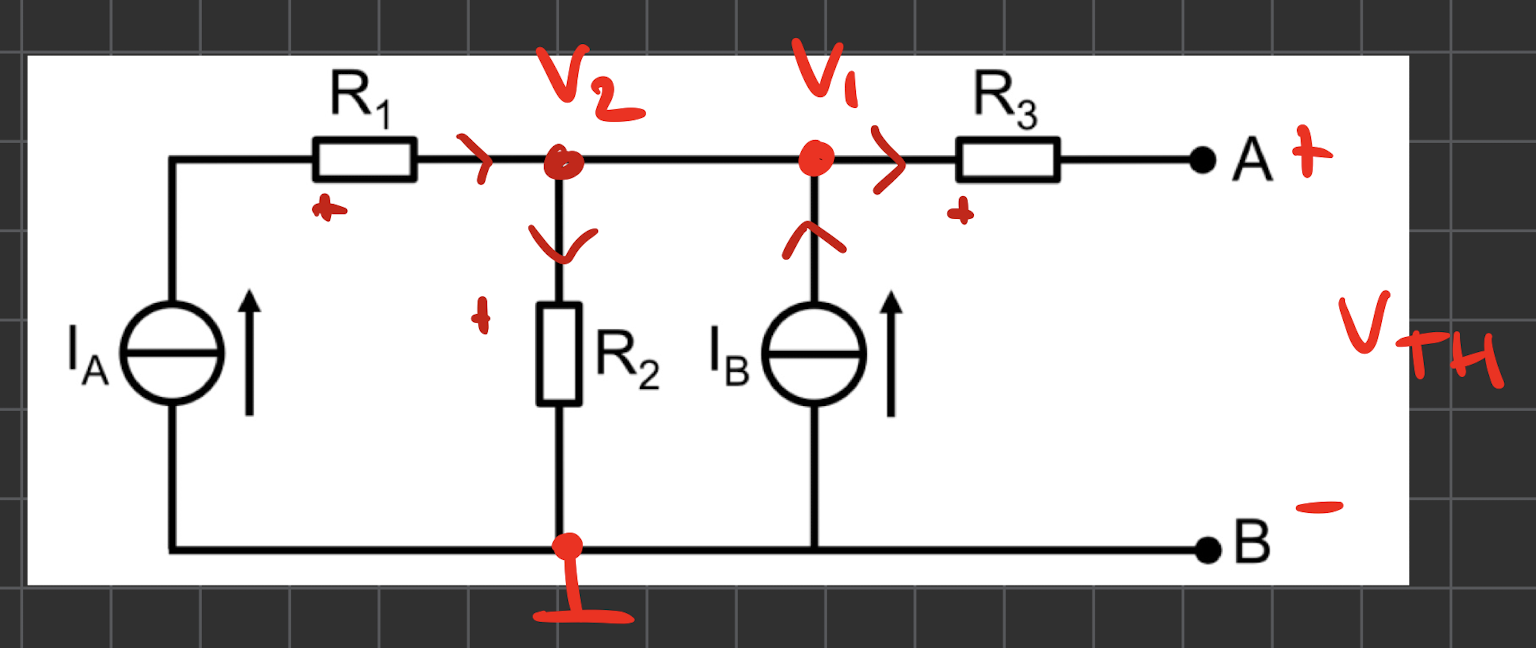
Sedan får jag genom KCL i V2 att (IA + IB) = IR2 , vilket slutligen ger VTH = VR2 = R2IR2 = R2(IA + IB).


