Beräkna tvärsnittsarean A(x) 2(2)
Hej, jag försöker lösa 2.18 b).
 Har kommit så långt (kort) som visas nedan. Vet inte om jag är helt fel ute med att använda stångens differentialekvation eller inte? Det jag tänkte var att man ska integrera ytterligare en gång för att utnyttja randvillkoren och . Får en känsla av att det är fel väg att gå eftersom det skulle bli rätt avancerat med tanke på att A(x) är bredvid.
Har kommit så långt (kort) som visas nedan. Vet inte om jag är helt fel ute med att använda stångens differentialekvation eller inte? Det jag tänkte var att man ska integrera ytterligare en gång för att utnyttja randvillkoren och . Får en känsla av att det är fel väg att gå eftersom det skulle bli rätt avancerat med tanke på att A(x) är bredvid.
Svaret i facit är:
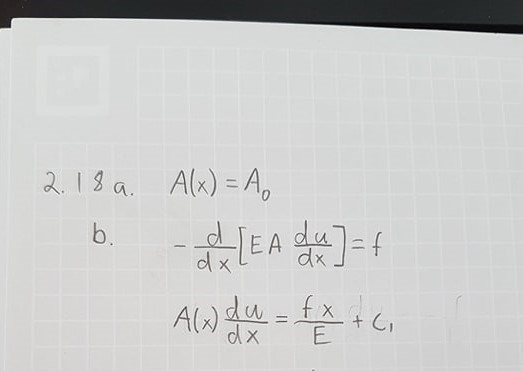
(märkte att jag glömt göra ena sidan negativ men det hjälper inte så mycket)
Varken derivata eller integraler är nödvändigt för det här problemet. Med hjälp av informationen i uppgiften kan du bestämma ett uttryck för axialförskjutningen . Vi kan även uttrycka axialförskjutningen med hjälp av töjningen , normalspänningen och slutligen tvärsnittsarean då vi har sambanden , och . Vi får då att:
Uttrycket för kraften är samma som i a)-uppgiften, och eftersom du tagit fram ett uttryck för är det bara att sätta in i ekvationen:
och sedan lösa ut för då allt annat är känt.
AlvinB skrev:Varken derivata eller integraler är nödvändigt för det här problemet. Med hjälp av informationen i uppgiften kan du bestämma ett uttryck för axialförskjutningen . Vi kan även uttrycka axialförskjutningen med hjälp av töjningen , normalspänningen och slutligen tvärsnittsarean då vi har sambanden , och . Vi får då att:
Uttrycket för kraften är samma som i a)-uppgiften, och eftersom du tagit fram ett uttryck för är det bara att sätta in i ekvationen:
och sedan lösa ut för då allt annat är känt.
Tack så jättemycket! Tycker den här var ovanligt svår för att vara en uppgift utan ledning i facit. Har du några tips för att se de här sambanden, alltså hur man ska börja uppgiften?
bigO skrev:Tack så jättemycket! Tycker den här var ovanligt svår för att vara en uppgift utan ledning i facit. Har du några tips för att se de här sambanden, alltså hur man ska börja uppgiften?
Vilka samband menar du? Menar du dessa:
Det är inget du ska "se" utan det är samband från grundläggande hållfasthetslära. Med andra ord första principer inom kontinuummekanik.
Ebola skrev:bigO skrev:Tack så jättemycket! Tycker den här var ovanligt svår för att vara en uppgift utan ledning i facit. Har du några tips för att se de här sambanden, alltså hur man ska börja uppgiften?
Vilka samband menar du? Menar du dessa:
Det är inget du ska "se" utan det är samband från grundläggande hållfasthetslära. Med andra ord första principer inom kontinuummekanik.
Tänkte snarare att man ska veta att man ska använda de istället för stångens differentialekvation. De tre formlerna känner jag till men har inte använt de för att lösa en sådan uppgift. Kanske bara är att testa vad som fungerar?
bigO skrev:Tänkte snarare att man ska veta att man ska använda de istället för stångens differentialekvation. De tre formlerna känner jag till men har inte använt de för att lösa en sådan uppgift. Kanske bara är att testa vad som fungerar?
En tumregel vid lösningsmetodik för mekanik, hållfasthetslära osv. är att ställa upp vad som är givet, vad som söks och vilka verktyg du har till hands. Bland dina verktyg ingår de samband som är relaterade till problemet. I det här fallet har du en axiell förskjutning och ett lineärt elastiskt material vilket direkt ger att dessa tre samband borde vara relevanta.
Det hör då till inlärningsprocessen att träna på att arbeta med relationerna och förstå hur de kan manipuleras för att anpassas till det problem man har till hands.
Ebola skrev:bigO skrev:Tänkte snarare att man ska veta att man ska använda de istället för stångens differentialekvation. De tre formlerna känner jag till men har inte använt de för att lösa en sådan uppgift. Kanske bara är att testa vad som fungerar?
En tumregel vid lösningsmetodik för mekanik, hållfasthetslära osv. är att ställa upp vad som är givet, vad som söks och vilka verktyg du har till hands. Bland dina verktyg ingår de samband som är relaterade till problemet. I det här fallet har du en axiell förskjutning och ett lineärt elastiskt material vilket direkt ger att dessa tre samband borde vara relevanta.
Det hör då till inlärningsprocessen att träna på att arbeta med relationerna och förstå hur de kan manipuleras för att anpassas till det problem man har till hands.
Okej tack :)
Måste fråga, fick du rätt svar med Alvins lösningsmetodik?
Ebola skrev:Måste fråga, fick du rätt svar med Alvins lösningsmetodik?
Ja, jag tog fram det linjära uttrycket för axialförskjutningen enligt uppgiften:
och satte sedan in det i ekvationen:
där .
Det gav
Varför har vi och inte i relationen?
Detta implicerar nämligen användning av det som kallas negativ snittyta, se bild nedan, kan du lista ut varför vi måste tillämpa en sådan?
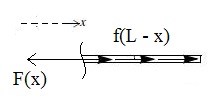
Ebola skrev:Varför har vi och inte i relationen?
Detta implicerar nämligen användning av det som kallas negativ snittyta, se bild nedan, kan du lista ut varför vi måste tillämpa en sådan?
Bra fråga, har ingen aning om varför jag gjorde så nu. Hur kan det bli rätt?
EDIT: Eller jo kraften ska väl vara högst i änden som är fäst? Eftersom den där måste bära hela kraften?
bigO skrev:Bra fråga, har ingen aning om varför jag gjorde så nu. Hur kan det bli rätt?
Visst är det spännande? Under tiden vi funderar på det kan vi återgå till den ursprungliga differentialekvationen du ställde upp och reda ut dina frågetecken. Vi har att:
Från relationen du själv ställt upp vet vi att
vilket slutligen ger oss en ekvation för arean:
Här har vi en okänd konstant men eftersom vi har randvillkoret att kan vi bestämma denna konstant. Med andra ord var det ett väldigt litet steg du missade.
Okej, vi får väl dock att
?
bigO skrev:Okej, vi får väl dock att
?
Ja precis, jag skrev fel och rättade. Vad får du för svar om du använder randvillkoret i din differentialekvation?
Ebola skrev:bigO skrev:Okej, vi får väl dock att
?
Ja precis, jag skrev fel och rättade. Vad får du för svar om du använder randvillkoret i din differentialekvation?
vilket blir samma :) Okej tack, tänkte aldrig på att man skulle göra ett uttryck för axialförskjutningen, skönt att se att jag tänkte rätt en bit i alla fall.
Tillbaka till det med negativ snittyta, är det inte som jag skrev i min edit? Att kraften ska vara högst i änden som är fäst? Eftersom den där måste bära hela kraften?
bigO skrev:Tillbaka till det med negativ snittyta, är det inte som jag skrev i min edit? Att kraften ska vara högst i änden som är fäst? Eftersom den där måste bära hela kraften?
Det är absolut så att den bär hela kraften i änden och det ger naturligtvis att om vi har en positiv snittyta får vi:
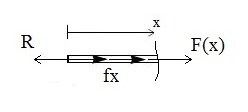 Vi har alltså en reaktionskraft från väggen vilken då kommer ge kraften som funktion av x som:
Vi har alltså en reaktionskraft från väggen vilken då kommer ge kraften som funktion av x som:
Snyggt jobbat, det visar att du har intuition för det här. Ganska lätt att bli lurad initialt va?



