Beräkna v max
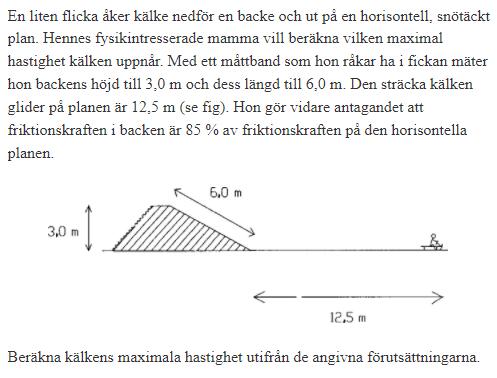
Jag tänker:
mgh = 0,5mv^2 +0,85f
12,5f = 0,5mv^2
f = (mv^2)/25
29,46m = m (v^2/2) + m(17v^2/500)
29,46 = (v^2/2) + (17v^2/500)
29,46 = v^2 ((1/2)+(1/25))
29,46 = 0,534v^2
v = 7,4 vilket är fel
Du behöver skriva mycket tydligare hur du tänker. Du behöver också definiera vad olika variabler betyder - vad är t ex "f"?
f = friktionskraften på den horisontella planen
jag tog 0,85*f eftersom det utgör friktionskraften i backen
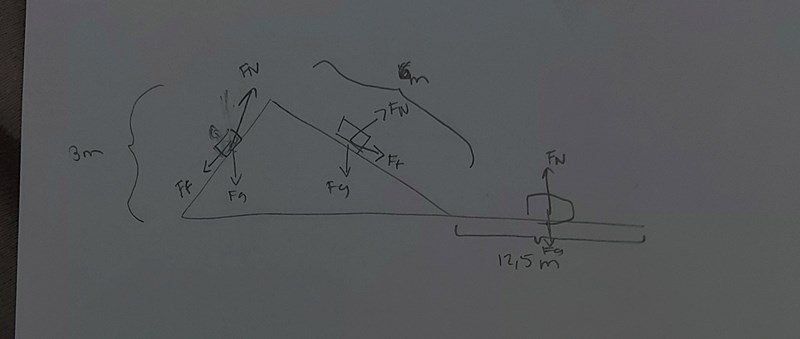
Börja med att rita ut vilka krafter som verkar på kälken, dels medan den är i backen, dels när den har kommit ut på plan mark. Lägg upp bilden här.
Lite korrigeringar i din figur:
När kälken glider nedför så verkar friktionskraften (Ff) mot rörelseriktningen, dvs upp längs backen inte neråt.
Du får en friktionskraft även när kälken glider på den plana delen.
Det ser ut som du tänkt rätt. Att det handlar om att omvandla mellan lägesenergi och rörelseenergi samt förluster som friktionen ger.
Var nånstans under kälkturen var hastigheten som störst?
Precis slutet av backen för då övergår all Ep till Ek
Inte riktigt allt. En del av Ep används för att övervinna friktionen på sträckan 6m.
Okej, men jag förstår ändå inte hur jag ska gå tillväga för att lösa uppgiften
Använd dig av att den lägesenergi som finns högst upp i backen har förvandlats till rörelseenergi plus friktion vid backens slut, och att rörelseenergin som fanns i början av den vågräta delen blir till friktion. Hastigheten i slutet av backen är samma sm hastigheten i början av den vågräta delen.