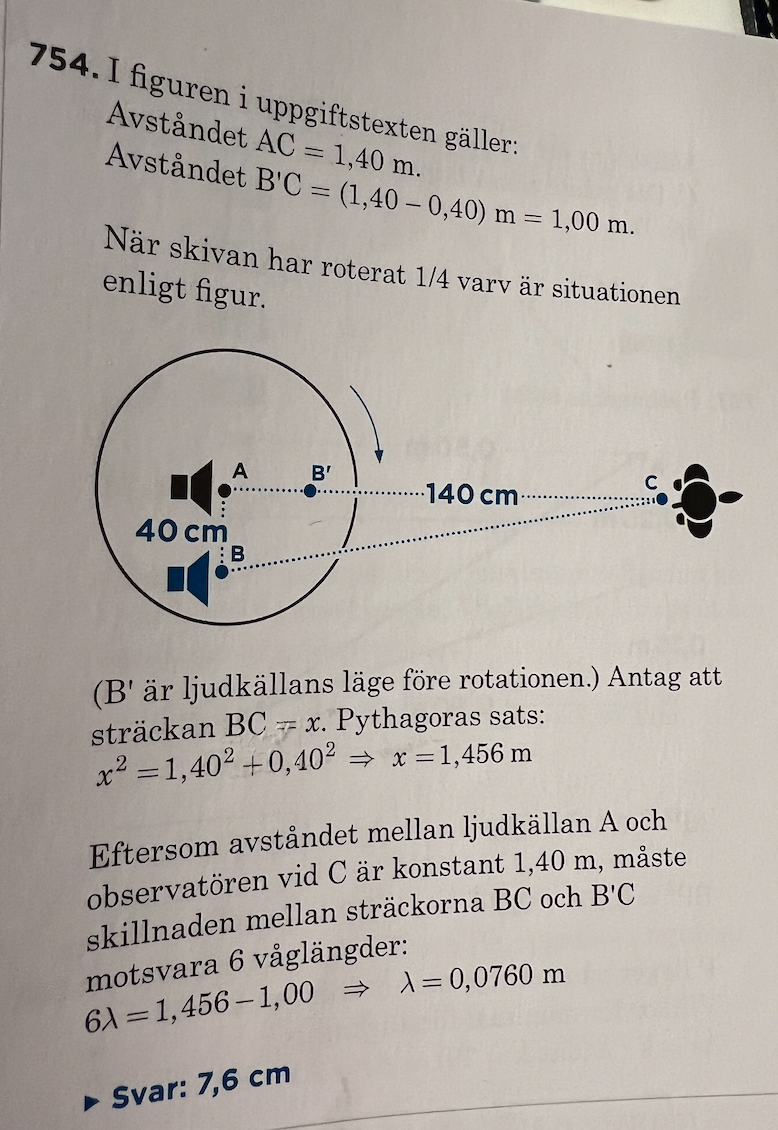
Beräkna våglängden på en roterande skiva...

Varför räcker det inte att titta på de faktiska avstånden från varje källa till observatören?
Och hur hänger det ihop med att det uppstår ett visst antal ljudmaxima (eller att facit säger att n = 6). Vart kommer detta ifrån? Varför BC och B'C? Se nedan för facit:
Visa spoiler
Hej! Jag kan inte öppna din bild av facit (ladda upp den som en bild istället), så jag vet inte hur lösningsförslaget ser ut.
Det är vägskillnaden mellan högtalarna och observatören som ska rymma ett jämnt antal våglängder för att observatören ska uppleva ljudmaximum. Men uppgiften talar inte om hur många våglängder som ryms i AB, bara att det är ett jämnt antal. Alltså kan man inte använda endast den informationen för att lösa uppgiften
Ledtråden får man istället genom att texten beskriver att "skillnaden i vägskillnad" jämfört med när skivan har roterat, rymmer 6 våglängder, och eftersom AC är lika långt i båda fallen, så är skillnaden i vägskillnad B'C-BC.
Hänger du med?
Här kommer facit:
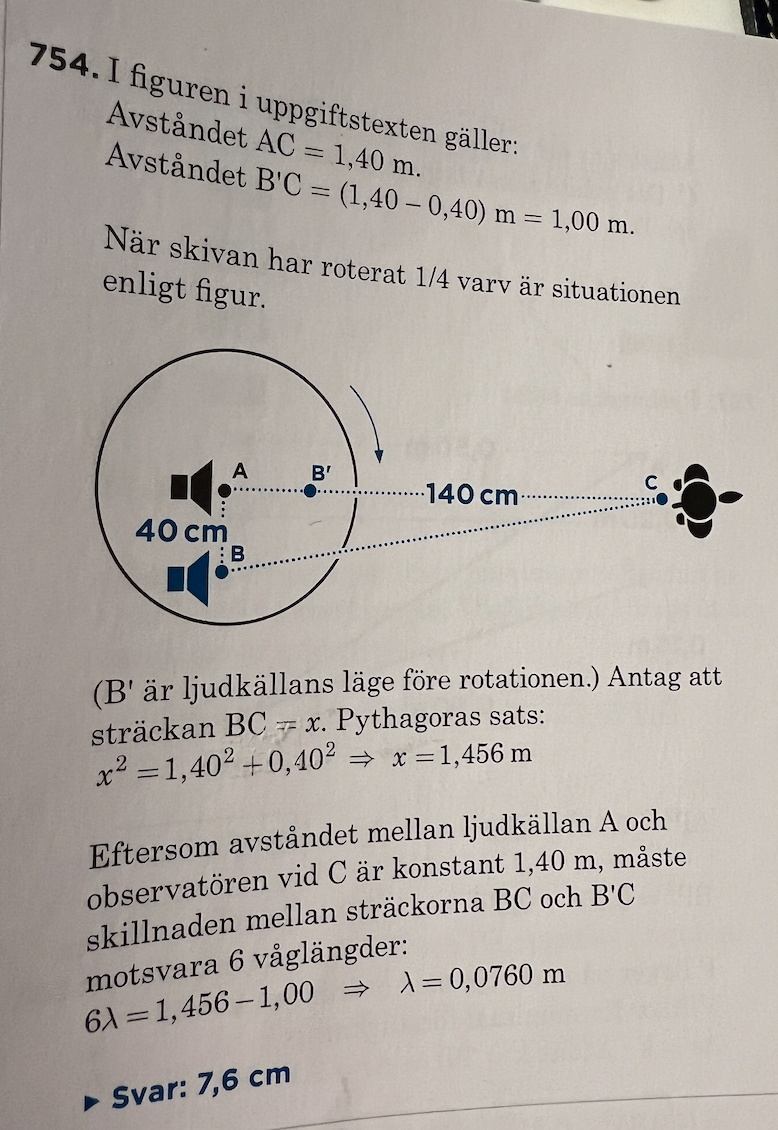
Du och facit använder alltså samma resonemang?
I mina ögon en luddigt formulerad uppgift. Jag tolkade den spontant inte som facit, men tänkte väl uppenbarligen fel?
"Då A, B och C befinner sig på samma räta linje (se figor) registrerar observatören ett ljudmaximum."
- Utgångspunkten, ljudmaximum #1.
"Observatören uppfattar sedan 5 ljudmaxima ..."
- Skivan roterar och observatören noterar ljudmaximum #2, #3, #4, #5, #6.
"... och befinner sig i det sjätte efter 1/4 varv av skivan."
- Stämmer bra! Det första i utgångspunkten och ytterligare fem. Det blir sex stycken. I så fall måste vägskillnaden motsvara fem våglängder.
Jo, jag har läst facit, men ville bara dela att jag lurades av uppgiften.
Anonym_15 skrev:Här kommer facit:
Du och facit använder alltså samma resonemang?
Ja, uppenbarligen resonerade facit likadant som jag :-)
Dock blev jag lite konfunderad över svaret (det var av den anledningen jag bad dig visa facit).
När jag hade fått fram svaret ville jag på något sätt kontrollera att det svar jag fick fram var rimligt. Jag beräknade då frekvensen till 340/0.076=4500Hz, vilket är en fullt hörbar ton. check!
Sedan tänkte jag kolla om det blev ljudmaximum med vägskillnaden 0.4m (vilket uppgiften säger att det blir). 0.4/0.076= 5.2, vilket _inte_ är ett heltal!!! Så jag tror uppgiftförfattaren inte tänkte färdigt när hen hittade på uppgiften, eftersom den information som finns i den inte är riktigt konsistent.