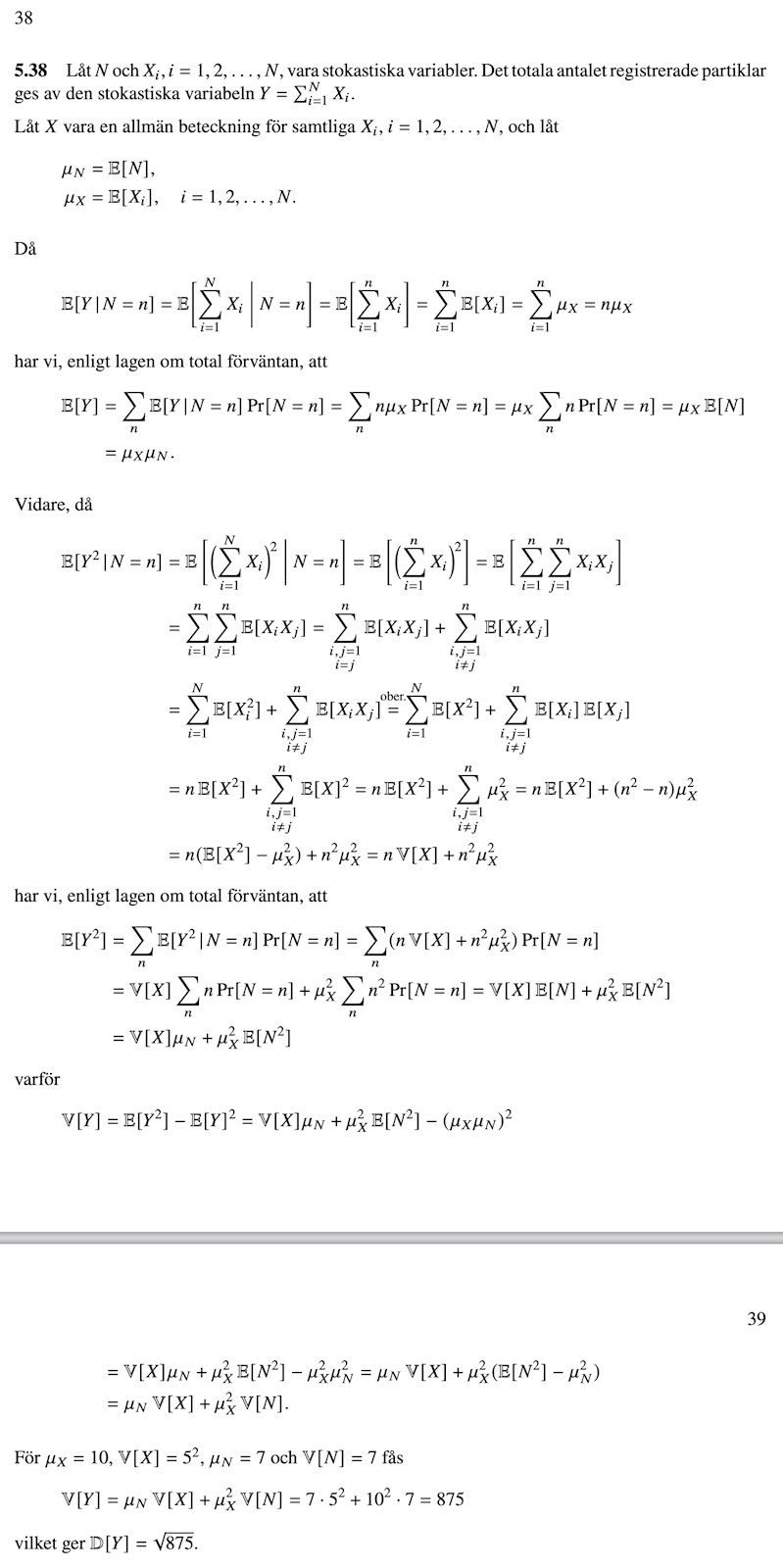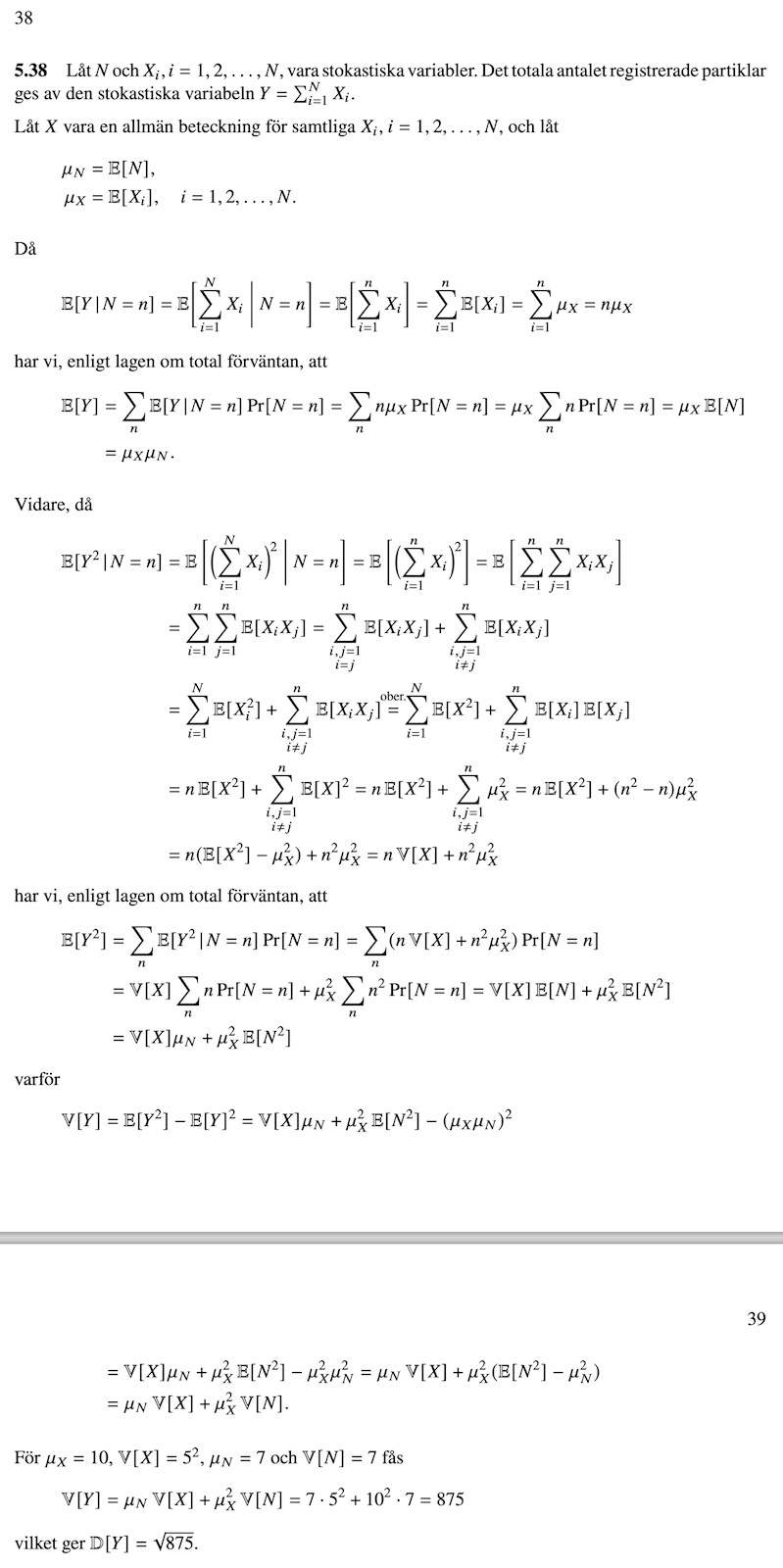Beräkna väntevärde och standardavvikelse för registrerade partiklar (Matematik/Universitet/Sannolikhet och Statistik)

Det gör man nog med hjälp av relativa värden av standarddeviation.

Pieter Kuiper skrev:
Det gör man nog med hjälp av relativa värden av standarddeviation.

Vad menar du med relativa värden av standarddeviation?

destiny99 skrev:
Pieter Kuiper skrev:
Det gör man nog med hjälp av relativa värden av standarddeviation.

Vad menar du med relativa värden av standarddeviation?

Jag gissar att D(X_i)=5 betyder att standarddeviationen är 5. Om väntevärdet E(X_i)=10, är den relativa standardavvikelsen 50 % eller 0,5.

Pieter Kuiper skrev:
destiny99 skrev:
Pieter Kuiper skrev:
Det gör man nog med hjälp av relativa värden av standarddeviation.

Vad menar du med relativa värden av standarddeviation?

Jag gissar att D(X_i)=5 betyder att standarddeviationen är 5. Om väntevärdet E(X_i)=10, är den relativa standardavvikelsen 50 % eller 0,5.

Vi vet att D(X)=sqrt(V(X)). Här vet vi att D(X_i)=5 så V(X_i)= 25? Sen vet vi att V(N)=7 så D(N)=sqrt(7). Men det känns om att vi söker D(NX_i)=sqrt(V(NX_i))

destiny99 skrev:
Men det känns om att vi söker D(NX_i)=sqrt(V(NX_i))

Jo. Och jag antar att det ska beräknas via den relativa standardavvikelsen $\sigma_{\rm rel} = \sqrt{\sigma^2_{\rm 1, rel} + \sigma^2_{\rm 2, rel}}$ .

Pieter Kuiper skrev:
destiny99 skrev:
Men det känns om att vi söker D(NX_i)=sqrt(V(NX_i))

Jo. Och jag antar att det ska beräknas via den relativa standardavvikelsen $\sigma_{\rm rel} = \sqrt{\sigma^2_{\rm 1, rel} + \sigma^2_{\rm 2, rel}}$ .

Chat föreslår dessa och får fram rätt svar. Mdn hur hittar man p_y(N)?

Här är även ett exempel ur kursboken.

destiny99 skrev:
rätt svar.

Så du har facit...

Jag gissar att det är ungefär 45.

Pieter Kuiper skrev:
destiny99 skrev:
rätt svar.

Så du har facit...

Jag gissar att det är ungefär 45.

Det är chatgpt , inte lösningsförslaget.

Jag vet inte riktigt vad du menar med att ChatGPT föreslagit något, har alltså ChatGPT föreslagit att du ska använda dessa satser?

Vi kan prova: om X är totala antalet partiklar vet du att $X|N = \sum_{i=1}^N X_i$

Kan du nu räkna ut V(X|N) och E(X|N)? Kom ihåg att $X_i$ är oberoende från varandra.

Tillägg: 29 apr 2025 07:53

Alltså, X i formeln kallas här också X och är totala antalet partiklar, medan Y i formeln är N (antalet inkommande partiklar)

Vad är svaret btw? Är det 45 som föreslagit ovan, eller närmare 30?

Hondel skrev:
Jag vet inte riktigt vad du menar med att ChatGPT föreslagit något, har alltså ChatGPT föreslagit att du ska använda dessa satser?

Vi kan prova: om X är totala antalet partiklar vet du att $X|N = \sum_{i=1}^N X_i$

Kan du nu räkna ut V(X|N) och E(X|N)? Kom ihåg att $X_i$ är oberoende från varandra.

Tillägg: 29 apr 2025 07:53

Alltså, X i formeln kallas här också X och är totala antalet partiklar, medan Y i formeln är N (antalet inkommande partiklar)

Ja asså chatgpt föreslog totala förväntan och sen någon annan sats i boken som jag inte minns namnet på.

Men jag fastnade på hur vi hittar V(X|N) och E(X|N). Jag antar att man ska göra som exemplet i #8.

Hondel skrev:
Vad är svaret btw? Är det 45 som föreslagit ovan, eller närmare 30?

Svaret är 70 och sqrt(875) på D(Y). Men hur man hittar D(Y) mha V(Y) är där jag körde fast och har svårt att kombinera sakerna ovan.

Okej, ja $\sqrt{875}$ var också det jag fick. D(Y) är standardavvikelsen av Y, vilket är $\sqrt{V(Y)}$ .

Men okej, låt oss kolla på hur man räknar E(X|N) och V(X|N). Du är med på att $X|N= \sum_i^N X_i$ ? Vad är väntevärdet/variansen av en summa av oberoende variabler?

Hondel skrev:
Okej, ja $\sqrt{875}$ var också det jag fick. D(Y) är standardavvikelsen av Y, vilket är $\sqrt{V(Y)}$ .

Men okej, låt oss kolla på hur man räknar E(X|N) och V(X|N). Du är med på att $X|N= \sum_i^N X_i$ ? Vad är väntevärdet/variansen av en summa av oberoende variabler?

Okej nej jag är inte med på hur X|N=X_i? Är detta en definition/sats eller? Var finns det i bloms bok isåfall? (Kommer inte ihåg alla saker)

Nej, $X|N=\sum_{i=1}^N X_i$ , notera summan.

X|N betyder X givet N. Alltså, givet att det kommer N partiklar, hur många totala partiklar blir det? Jo, varje inkommande partikel ger upphov till $X_i$ partiklar, så om det totalt är N inkommande partiklar kommer det blir en summa mellan i=1 till N och varje term är $X_i$

Alltså, vi summerar bara antalet uppkomna partiklar från varje inkommande partikel, och totalt är det N stycken inkomna partiklar

Hondel skrev:
Nej, $X|N=\sum_{i=1}^N X_i$ , notera summan.

X|N betyder X givet N. Alltså, givet att det kommer N partiklar, hur många totala partiklar blir det? Jo, varje inkommande partikel ger upphov till $X_i$ partiklar, så om det totalt är N inkommande partiklar kommer det blir en summa mellan i=1 till N och varje term är $X_i$

Alltså, vi summerar bara antalet uppkomna partiklar från varje inkommande partikel, och totalt är det N stycken inkomna partiklar

Aa ok.

Så, kan du nu räkna ut E(X|N) och V(X|N)?

Hondel skrev:
Så, kan du nu räkna ut E(X|N) och V(X|N)?

E(X|N)=E(N*X_i) men V(X|N) vet jag inte

Hur kom du fram till väntevärdet? Du borde kunna använda samma metod för variansen

Man ska kanske vara lite försiktig med notationen och se till att N är utanför, alltså $E(X|N)=N*E(X_i)$ I och med att det är väntevärdet med avseende på X vi räknar, så man inte blir förvirrad och tar väntevärdet på N eller liknande

Hondel skrev:
Man ska kanske vara lite försiktig med notationen och se till att N är utanför, alltså $E(X|N)=N*E(X_i)$ I och med att det är väntevärdet med avseende på X vi räknar, så man inte blir förvirrad och tar väntevärdet på N eller liknande

Aa ok jag förstår. Men i frågan är E(N) givet också och varför tar du ut N framför E(X_i)? Jag vet att det finns ett samband som säger (EXY)=E(X)×E(Y) om X och Y är oberoende.

Hm, okej flera grejer som pågår nu. Jag ska försöka reda ut.

Visst stämmer det att väntevärdet av en produkt av två oberoende variabler är produkten av deras väntevärden. Dock är inte totala antalet partiklar $X$ produkten $N\cdot X_i$ : det skulle betyda att alla inkommande partiklar ger upphov till samma antalet partiklar $X_i$ . Som jag sagt tidigare, $X$ , givet $N$ (vilket betecknas $X|N$ ) är summan $\sum_{i=1}^N X_i$ .

Om du då vill beräkna väntevärdet $E[X]$ kan du använda lagen om total förväntan som säger att $E[X]=E[E[X|N]]$ . Dvs, första beräknar du $E[X|N]$ , dvs, du ser $N$ som ett fixt värde och beräknar väntevärdet för detta (vilket då kommer bero på värdet N), och sedan beräknar du väntevärdet av detta. Jag demonstrerar hur man skulle göra detta i din uppgift:

$E[X|N] = E[\sum_{i=1}^N X_i] = \sum_{i=1}^N E[X_i] = N\cdot E[X_i] = N\cdot 10$ där jag utnyttjat att väntevärdet av en summa är summan av väntevärden (dvs, jag kan flytta in väntevärdet innanför summan), och alla $X_i$ har samma väntevärden.

Detta beror alltså på N. Så nu tar vi väntevärdet på detta:

$E[10N] = 10E[N] = 70$ . (konstanten 10 kan bara flyttas utanför väntevärdet)

I detta fall blev det lika med det du fick fram, men jag skulle säga att hur du motiverar det är inte riktigt korrekt.

Okej, nu kan vi kolla på variansen. Jag visade ovan vad $E[X|N]$ är. Vi kan beräkna $V[X|N]$ på liknande sätt:

$V[X|N] = V[\sum_{i=1}^N X_i] = \sum_{i=1}^N V[X_i] = N\cdot V[X_i] = N \cdot 5^2$ , där jag utnyttjat att variansen av en summa av oberoende variabler är summan av varianser (och $X_i$ är oberoende), samt att standardavvikelsen $D[X_i]$ är given, och $V[X_i]=D[X_i]^2$ .

Så, kan du med hjälp av detta fortsätta räkna ut $V[X] = E[V[X|N]] + V[E[X|N]]$ ?

Hondel skrev:
Hm, okej flera grejer som pågår nu. Jag ska försöka reda ut.

Visst stämmer det att väntevärdet av en produkt av två oberoende variabler är produkten av deras väntevärden. Dock är inte totala antalet partiklar $X$ produkten $N\cdot X_i$ : det skulle betyda att alla inkommande partiklar ger upphov till samma antalet partiklar $X_i$ . Som jag sagt tidigare, $X$ , givet $N$ (vilket betecknas $X|N$ ) är summan $\sum_{i=1}^N X_i$ .

Om du då vill beräkna väntevärdet $E[X]$ kan du använda lagen om total förväntan som säger att $E[X]=E[E[X|N]]$ . Dvs, första beräknar du $E[X|N]$ , dvs, du ser $N$ som ett fixt värde och beräknar väntevärdet för detta (vilket då kommer bero på värdet N), och sedan beräknar du väntevärdet av detta. Jag demonstrerar hur man skulle göra detta i din uppgift:

$E[X|N] = E[\sum_{i=1}^N X_i] = \sum_{i=1}^N E[X_i] = N\cdot E[X_i] = N\cdot 10$ där jag utnyttjat att väntevärdet av en summa är summan av väntevärden (dvs, jag kan flytta in väntevärdet innanför summan), och alla $X_i$ har samma väntevärden.

Detta beror alltså på N. Så nu tar vi väntevärdet på detta:

$E[10N] = 10E[N] = 70$ . (konstanten 10 kan bara flyttas utanför väntevärdet)

I detta fall blev det lika med det du fick fram, men jag skulle säga att hur du motiverar det är inte riktigt korrekt.

Okej, nu kan vi kolla på variansen. Jag visade ovan vad $E[X|N]$ är. Vi kan beräkna $V[X|N]$ på liknande sätt:

$V[X|N] = V[\sum_{i=1}^N X_i] = \sum_{i=1}^N V[X_i] = N\cdot V[X_i] = N \cdot 5^2$ , där jag utnyttjat att variansen av en summa av oberoende variabler är summan av varianser (och $X_i$ är oberoende), samt att standardavvikelsen $D[X_i]$ är given, och $V[X_i]=D[X_i]^2$ .

Så, kan du med hjälp av detta fortsätta räkna ut $V[X] = E[V[X|N]] + V[E[X|N]]$ ?

Tack för hjälpen. Återkommer om det uppstår annan fråga. Har inte lyckats lösa frågan men jag avvaktar med den känner jag.

Denna uppgift är rätt ”stökig”, men då jag ändå räknar mig igenom Blom skall jag se på denna.

destiny99 skrev:

Hej!

Jag lyckades med att hitta väntevärdet mha E(NX_i)=E(N)E(X_i)=70 men fastnade med att hitta standardavvikelse. Hur tänker man där?

gör så! Återkom gärna.

Konfunderad... du svarar dig själv?

Trinity2 skrev:
Konfunderad... du svarar dig själv?

Oj det e sant. Meningen var att svara på ditt inlägg där du skrev

"Denna uppgift är rätt ”stökig”, men då jag ändå räknar mig igenom Blom skall jag se på denna".

destiny99 skrev:
Trinity2 skrev:
Konfunderad... du svarar dig själv?

Oj det e sant. Meningen var att svara på ditt inlägg där du skrev

"Denna uppgift är rätt ”stökig”, men då jag ändå räknar mig igenom Blom skall jag se på denna".

Då är jag med. Skall kolla in i e.m.

destiny99 skrev:
Trinity2 skrev:
Konfunderad... du svarar dig själv?

Oj det e sant. Meningen var att svara på ditt inlägg där du skrev

"Denna uppgift är rätt ”stökig”, men då jag ändå räknar mig igenom Blom skall jag se på denna".

Något så här, typ;

Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Konfunderad... du svarar dig själv?

Oj det e sant. Meningen var att svara på ditt inlägg där du skrev

"Denna uppgift är rätt ”stökig”, men då jag ändå räknar mig igenom Blom skall jag se på denna".

Något så här, typ;

Skulle du kunna förklara typ steg för steg? Jag fattar inte mycket av allt justnu speciellt när det gäller att ta reda på standardavvikelse och sånt.

destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Konfunderad... du svarar dig själv?

Oj det e sant. Meningen var att svara på ditt inlägg där du skrev

"Denna uppgift är rätt ”stökig”, men då jag ändå räknar mig igenom Blom skall jag se på denna".

Något så här, typ;

Skulle du kunna förklara typ steg för steg? Jag fattar inte mycket av allt justnu.

Det blir en lång föreläsning isf och jag skall just ut i solen lite.

Men, studera definitoner av väntevärde och varians samt betingat väntevärde och varians och lagen om total förväntan. Det måste stå något i boken, man kna inte klara detta rakt av utan en teori så det bör stå om ni inte har Bloms bok, där det säkert står.

Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
destiny99 skrev:
Trinity2 skrev:
Konfunderad... du svarar dig själv?

Oj det e sant. Meningen var att svara på ditt inlägg där du skrev

"Denna uppgift är rätt ”stökig”, men då jag ändå räknar mig igenom Blom skall jag se på denna".

Något så här, typ;

Skulle du kunna förklara typ steg för steg? Jag fattar inte mycket av allt justnu.

Det blir en lång föreläsning isf och jag skall just ut i solen lite.

Men, studera definitoner av väntevärde och varians samt betingat väntevärde och varians och lagen om total förväntan. Det måste stå något i boken, man kna inte klara detta rakt av utan en teori så det bör stå om ni inte har Bloms bok, där det säkert står.

I bloms bok förklaras inte detta så väl tyvärr. Jag tog upp frågan med någon annan också och ingen av oss kunde få fram standardavvikelse eller variansen. Tack ändå för hjälpen.

Du kan fortsätta på min lösning kanske

vad är E[25N]? Vad är V[10N]?

Hondel skrev:
Du kan fortsätta på min lösning kanske

vad är E[25N]? Vad är V[10N]?

Det beror på vad du menar med E(25N)? Menar du 25×E(N)? Var kommer 25 ifrån? Gällande V(10N) så minns jag inte denna regel a^2V(b) gäller här , det var så att det var 10^2×V(N).

Jag menar E[25N], alltså, väntevärdet av 25 gånger N. Vilket är lika med 25E[N]. Och ja det stämmer att V[10N]=100V[N].

25N kommer från $5^2N$ ovan. Jag skrev det på datorn och när jag kollar på inlägget från mobilen är det helt oförståeligt, matematiken är väldigt konstigt formaterad.

Hondel skrev:
Jag menar E[25N], alltså, väntevärdet av 25 gånger N. Vilket är lika med 25E[N]. Och ja det stämmer att V[10N]=100V[N].

25N kommer från $5^2N$ ovan. Jag skrev det på datorn och när jag kollar på inlägget från mobilen är det helt oförståeligt, matematiken är väldigt konstigt formaterad.

Men i princip kom jag fram till att E[X|N]=10N och V[X|N]=25N. Och det betyder att V[E[X|N]]=V[10N] och E[V[X|N]=E[25N]. Med det kan du få V[X]=V[E[X|N]] + E[V[X|N]]

Så V(X)=V(10N)+E(25N)?

destiny99 skrev:
Hondel skrev:
Jag menar E[25N], alltså, väntevärdet av 25 gånger N. Vilket är lika med 25E[N]. Och ja det stämmer att V[10N]=100V[N].

25N kommer från $5^2N$ ovan. Jag skrev det på datorn och när jag kollar på inlägget från mobilen är det helt oförståeligt, matematiken är väldigt konstigt formaterad.

Men i princip kom jag fram till att E[X|N]=10N och V[X|N]=25N. Och det betyder att V[E[X|N]]=V[10N] och E[V[X|N]=E[25N]. Med det kan du få V[X]=V[E[X|N]] + E[V[X|N]]

Så V(X)=V(10N)+E(25N)?

Jepp

Hondel skrev:
destiny99 skrev:
Hondel skrev:
Jag menar E[25N], alltså, väntevärdet av 25 gånger N. Vilket är lika med 25E[N]. Och ja det stämmer att V[10N]=100V[N].

25N kommer från $5^2N$ ovan. Jag skrev det på datorn och när jag kollar på inlägget från mobilen är det helt oförståeligt, matematiken är väldigt konstigt formaterad.

Men i princip kom jag fram till att E[X|N]=10N och V[X|N]=25N. Och det betyder att V[E[X|N]]=V[10N] och E[V[X|N]=E[25N]. Med det kan du få V[X]=V[E[X|N]] + E[V[X|N]]

Så V(X)=V(10N)+E(25N)?

Jepp

Men då blir det V(X)=10^2V(N)+25E(N)=100×7+25×7=875

så D(X)=sqrt(875)

Yes, och det var väl korrekt svar också?

Hondel skrev:j
Yes, och det var väl korrekt svar också?

Ja precis:)