Beräkna värde av sinus (Matematik/Matte 3/Trigonometri)

Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?

Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.

Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.

Försökte det, men det blev krångligare kändes det som

Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som

Visa vad du gjorde.

Korra skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som
Visa vad du gjorde.

Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte

Supporter skrev:
Korra skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som
Visa vad du gjorde.
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte

Hur långt är det mellan 7pi/2 och 3pi/2?

Supporter skrev:

Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte

Du tänker nog rätt.

Vinkeln 7pi/2 är inte samma som vinkeln 3pi/2, men de har samma sinusvärde.

Det är viktigt att du förstår varför de har det. Be gärna om förklaring om du inte kommer på själv varför.

Det som efterfrågas är sedan just detta sinusvärde, dvs inte ett talpar som du har skrivit.

Yngve skrev:
Supporter skrev:
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte
Du tänker nog rätt.
Vinkeln 7pi/2 är inte samma som vinkeln 3pi/2, men de har samma sinusvärde.
Det är viktigt att du förstår varför de har det. Be gärna om förklaring om du inte kommer på själv varför.
Det som efterfrågas är sedan just detta sinusvärde, dvs inte ett talpar som du har skrivit.

Om man delar in enhetscirkeln i fyra delar så hamnar 7pi/2 och 3pi/2 i samma del, dvs samma sinusvärde som är -1. Är det rätt och svara som jag gjort då? Hur ska man veta vart 7pi/2 är på ett mer effektivt sätt? Finns det någon smart sätt att enkelt och snabbt lösa liknande uppgifter?

Supporter skrev:

Om man delar in enhetscirkeln i fyra delar så hamnar 7pi/2 och 3pi/2 i samma del, dvs samma sinusvärde som är -1. Är det rätt och svara som jag gjort då? Hur ska man veta vart 7pi/2 är på ett mer effektivt sätt? Finns det någon smart sätt att enkelt och snabbt lösa liknande uppgifter?

Ja -1 är rätt svar.

Eftersom sinusfunktionen är periodisk med perioden $2\pi$ så gäller att $sin(v)=sin(v+2\pi)$ .

Därför kan du lägga till eller dra ifrån ett helt antal multiplar av $2\pi$ till en vinkel $v$ utan att ändra sinusvärdet.

Det betyder att $sin(\frac{7\pi}{2})=sin(\frac{7\pi}{2}-2\pi)=sin(\frac{3\pi}{2})$ .

Supporter skrev:
Yngve skrev:
Supporter skrev:
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte
Du tänker nog rätt.
Vinkeln 7pi/2 är inte samma som vinkeln 3pi/2, men de har samma sinusvärde.
Det är viktigt att du förstår varför de har det. Be gärna om förklaring om du inte kommer på själv varför.
Det som efterfrågas är sedan just detta sinusvärde, dvs inte ett talpar som du har skrivit.
Om man delar in enhetscirkeln i fyra delar så hamnar 7pi/2 och 3pi/2 i samma del, dvs samma sinusvärde som är -1. Är det rätt och svara som jag gjort då? Hur ska man veta vart 7pi/2 är på ett mer effektivt sätt? Finns det någon smart sätt att enkelt och snabbt lösa liknande uppgifter?

Vad är ditt svar på frågan jag ställde?

Laguna skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som
Visa vad du gjorde.
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte
Hur långt är det mellan 7pi/2 och 3pi/2?

Ingen aning? Jag skrev bara ut de 4 första väderna i enhetscirkeln sen delade dem tills jag hittade 7pi/2

Yngve skrev:
Supporter skrev:
Om man delar in enhetscirkeln i fyra delar så hamnar 7pi/2 och 3pi/2 i samma del, dvs samma sinusvärde som är -1. Är det rätt och svara som jag gjort då? Hur ska man veta vart 7pi/2 är på ett mer effektivt sätt? Finns det någon smart sätt att enkelt och snabbt lösa liknande uppgifter?
Ja -1 är rätt svar.
Eftersom sinusfunktionen är periodisk med perioden $2\pi$ så gäller att $sin(v)=sin(v+2\pi)$ .
Därför kan du lägga till eller dra ifrån ett helt antal multiplar av $2\pi$ till en vinkel $v$ utan att ändra sinusvärdet.
Det betyder att $sin(\frac{7\pi}{2})=sin(\frac{7\pi}{2}-2\pi)=sin(\frac{3\pi}{2})$ .

Förstod inte riktigt vad du mena? Ändras inte sinusvärdet om man lägger till en vinkel som är större än 90°? Och allt inom 90° har samma sinusvärde?

Allt inom 90 grader har definitivt inte samma sinusvärde.

Supporter skrev:
Laguna skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som
Visa vad du gjorde.
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte
Hur långt är det mellan 7pi/2 och 3pi/2?
Ingen aning? Jag skrev bara ut de 4 första väderna i enhetscirkeln sen delade dem tills jag hittade 7pi/2

Ingen aning? Har du hört talas om subtraktion? (minus)

Laguna skrev:
Supporter skrev:
Laguna skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som
Visa vad du gjorde.
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte
Hur långt är det mellan 7pi/2 och 3pi/2?
Ingen aning? Jag skrev bara ut de 4 första väderna i enhetscirkeln sen delade dem tills jag hittade 7pi/2
Ingen aning? Har du hört talas om subtraktion? (minus)

Subtraktion, ja. Men hur har subtraktion något med detta att göra?

Smaragdalena skrev:
Allt inom 90 grader har definitivt inte samma sinusvärde.

Okej då är jag ute och cyklar...

Supporter skrev:

Förstod inte riktigt vad du mena? Ändras inte sinusvärdet om man lägger till en vinkel som är större än 90°?

...

Jo sinusvärdet ändras då vinkeln ändras. Men samma sinusvärde återkommer då vinkeln ändras med ett helt varv, dvs med $2\pi$ radianer.

Du kan läsa mer om det här.

Har du läst igenom kapitlet om trigonometri på matteboken.se, alternativt i din egen mattebok? Det verkar som om du borde börja med det. Jag gillar särskilt enhetscirkeln.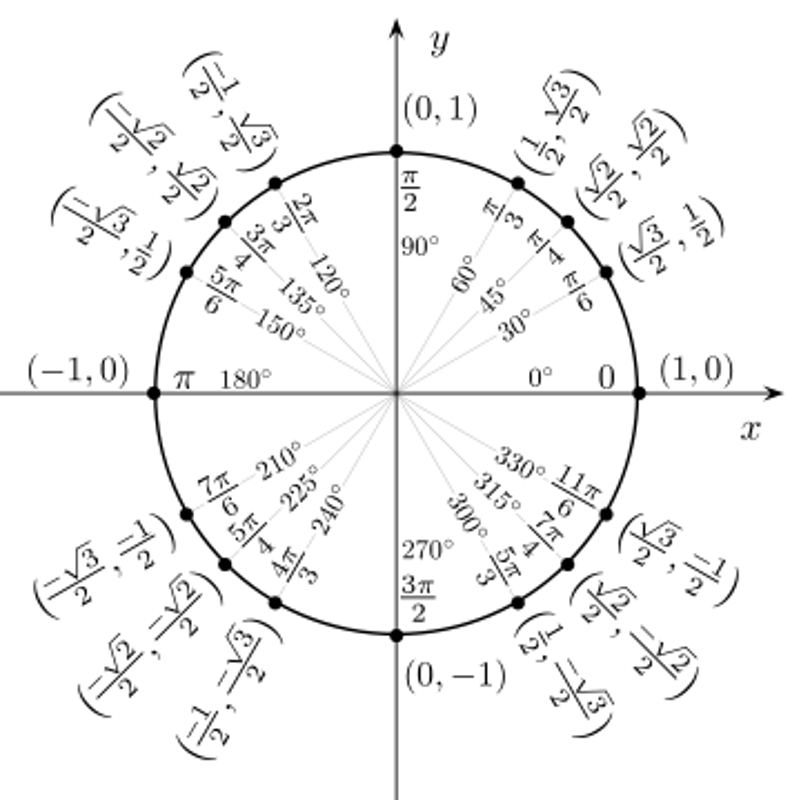

Supporter skrev:
Laguna skrev:
Supporter skrev:
Laguna skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som
Visa vad du gjorde.
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte
Hur långt är det mellan 7pi/2 och 3pi/2?
Ingen aning? Jag skrev bara ut de 4 första väderna i enhetscirkeln sen delade dem tills jag hittade 7pi/2
Ingen aning? Har du hört talas om subtraktion? (minus)
Subtraktion, ja. Men hur har subtraktion något med detta att göra?

Jag vill att du räknar ut 7pi/2 minus 3pi/2.

Laguna skrev:
Supporter skrev:
Laguna skrev:
Supporter skrev:
Laguna skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Korra skrev:
Supporter skrev:
Vilket värde har $\sin \frac{n π}{2}$ om n=7 ?

Hur ska man beräkna detta utan en miniräknare?
Rita en enhetscirkel eller kolla standardvärden för olika vinklar på formelbladet skulle jag gissa på.
Försökte det, men det blev krångligare kändes det som
Visa vad du gjorde.
Ritade en enhetscirkel där 7pi/2 hamnade nära 3pi/2 som är (0,-1) i enhetscirkeln så jag skrev det som svar men är osäker. Försökte rita det i tråden men det gick inte
Hur långt är det mellan 7pi/2 och 3pi/2?
Ingen aning? Jag skrev bara ut de 4 första väderna i enhetscirkeln sen delade dem tills jag hittade 7pi/2
Ingen aning? Har du hört talas om subtraktion? (minus)
Subtraktion, ja. Men hur har subtraktion något med detta att göra?
Jag vill att du räknar ut 7pi/2 minus 3pi/2.

$\frac{7 π}{2} - \frac{3 π}{2} = \frac{7 π - 3 π}{2} = \frac{4 π}{2}$

Smaragdalena skrev:
Har du läst igenom kapitlet om trigonometri på matteboken.se, alternativt i din egen mattebok? Det verkar som om du borde börja med det. Jag gillar särskilt enhetscirkeln.

Har stött på den, ska läsa länken du bifogade

Yngve skrev:
Supporter skrev:
Förstod inte riktigt vad du mena? Ändras inte sinusvärdet om man lägger till en vinkel som är större än 90°?
...
Jo sinusvärdet ändras då vinkeln ändras. Men samma sinusvärde återkommer då vinkeln ändras med ett helt varv, dvs med $2\pi$ radianer.
Du kan läsa mer om det här.

Okej förstår vad du menar med att den ändras om vinkeln ändras men om det går ett helt varv så är den på samma plats som den började på vilket ger den samma sinusvärde då. Ska läsa länken