Beräkna volymen av kroppen x^2+y^2<z<(3/4)-x-2y
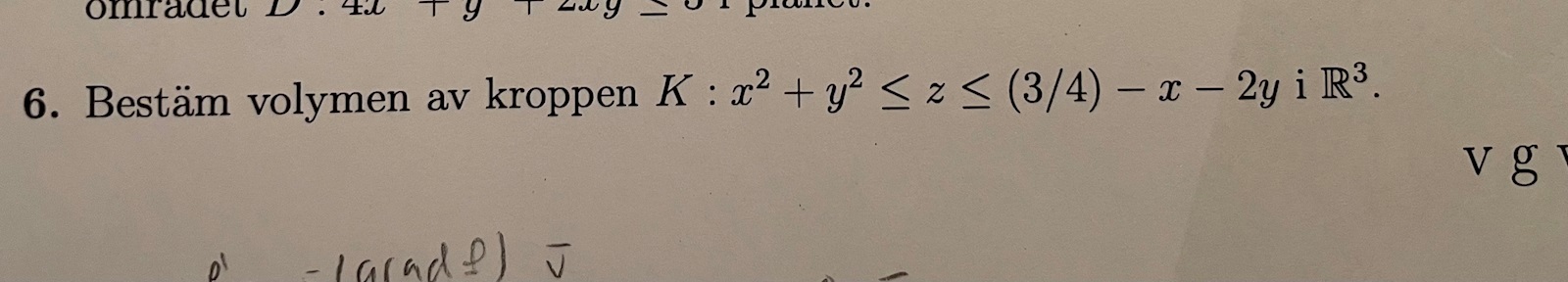
Här blev jag lite osäker på ifall jag har gjort rätt med ny projektion. Stämmer min lösning?

Hej,
För att beräkna volymen av kroppen definierad av �2+�2<�<34−�−2�x2+y2<z<43−x−2y, kan vi använda en trippelintegral över det givna området.
Den generella formeln för volymen av en kropp �E definierad av �1(�,�)<�<�2(�,�)g1(x,y)<z<g2(x,y) är:
�=∬�[�2(�,�)−�1(�,�)] ��V=D∬[g2(x,y)−g1(x,y)]dA
Här är �D det område i xy-planet som projektionen av kroppen på xy-planet täcker, och ��dA är elementarean i xy-planet.
I det här fallet är �1(�,�)=�2+�2g1(x,y)=x2+y2 och �2(�,�)=34−�−2�g2(x,y)=43−x−2y.
Så, volymen �V blir:
�=∬�[34−�−2�−(�2+�2)] ��V=D∬[43−x−2y−(x2+y2)]dA
För att beräkna detta krävs en specifik region �D i xy-planet som täcks av projektionen av kroppen. Utan en specificerad region är det svårt att ge en exakt numerisk lösning.
Om du har en specifik region i åtanke, kan vi fortsätta med att beräkna integralen.
Låt oss anta att �D är den cirkulära regionen definierad av �2+�2<34x2+y2<43. Denna cirkel täcker hela området definierat av �2+�2<�<34−�−2�x2+y2<z<43−x−2y.
Därmed kan vi skriva om volymformeln som:
�=∬�(34−�−2�−(�2+�2)) ��V=D∬(43−x−2y−(x2+y2))dA
För att utföra detta dubbelintegral över �D, kan vi använda polära koordinater eftersom det är en cirkulär region.
I polära koordinater är �=�cos(�)x=rcos(θ) och �=�sin(�)y=rsin(θ). Elementarean ��dA i polära koordinater är �����rdrdθ.
Substituera in polära koordinater i integralen:
�=∫02�∫034(34−�cos(�)−2�sin(�)−�2)� �� ��V=∫02π∫043(43−rcos(θ)−2rsin(θ)−r2)rdrdθ
Detta ger oss en dubbelintegral i polära koordinater över den specificerade regionen �D. Nu kan du beräkna denna integral för att få volymen av den givna kroppen.
Tedrez1202 skrev:Hej,
För att beräkna volymen av kroppen definierad av �2+�2<�<34−�−2�x2+y2<z<43−x−2y, kan vi använda en trippelintegral över det givna området.
Den generella formeln för volymen av en kropp �E definierad av �1(�,�)<�<�2(�,�)g1(x,y)<z<g2(x,y) är:
�=∬�[�2(�,�)−�1(�,�)] ��V=D∬[g2(x,y)−g1(x,y)]dA
Här är �D det område i xy-planet som projektionen av kroppen på xy-planet täcker, och ��dA är elementarean i xy-planet.
I det här fallet är �1(�,�)=�2+�2g1(x,y)=x2+y2 och �2(�,�)=34−�−2�g2(x,y)=43−x−2y.
Så, volymen �V blir:
�=∬�[34−�−2�−(�2+�2)] ��V=D∬[43−x−2y−(x2+y2)]dA
För att beräkna detta krävs en specifik region �D i xy-planet som täcks av projektionen av kroppen. Utan en specificerad region är det svårt att ge en exakt numerisk lösning.
Om du har en specifik region i åtanke, kan vi fortsätta med att beräkna integralen.
Låt oss anta att �D är den cirkulära regionen definierad av �2+�2<34x2+y2<43. Denna cirkel täcker hela området definierat av �2+�2<�<34−�−2�x2+y2<z<43−x−2y.
Därmed kan vi skriva om volymformeln som:
�=∬�(34−�−2�−(�2+�2)) ��V=D∬(43−x−2y−(x2+y2))dA
För att utföra detta dubbelintegral över �D, kan vi använda polära koordinater eftersom det är en cirkulär region.
I polära koordinater är �=�cos(�)x=rcos(θ) och �=�sin(�)y=rsin(θ). Elementarean ��dA i polära koordinater är �����rdrdθ.
Substituera in polära koordinater i integralen:
�=∫02�∫034(34−�cos(�)−2�sin(�)−�2)� �� ��V=∫02π∫043(43−rcos(θ)−2rsin(θ)−r2)rdrdθ
Detta ger oss en dubbelintegral i polära koordinater över den specificerade regionen �D. Nu kan du beräkna denna integral för att få volymen av den givna kroppen.
Jag är ledsen men kan inte läsa något av vad du skrivit. Är bara massa frågetecken på symboler du skrivit in

