Beräkning av arc-funktioner
Anm: Vet inte riktigt om detta ska placeras i Ma4 eller Uni då det är ett tal från en repetitionskurs av gymnasiematten men på universitetet.
Har med delfrågor jag klarat av för bakgrund/förståelse.
Upg: Låt α=arcsin1314 och β = arccos 17
a) Beräkna tan(α+β)
b) Bestäm alla vinklar med samma tangensvärde som i (a).
c) Stäng in α+β i ett öppet intervall av längd högst π.
d) Beräkna α+β
Det är c & d jag har problem med - vet inte om det är bäst att skapa separata trådar för dem eller göra som nu där jag har båda delfrågorna (delfrågorna bygger ju på varandra) i en tråd.
a) fick jag fram via två rätvinkliga trianglar och utvecklingen tan(α+β)=tanα+tanβ1-tanαtanβ=-1√3
b) Svaret i a) kommer med en standardvinkel: tan(-1√3)=-tan(1√3)=-π6+π n, n∈ℤ
c) Förstår jag inte frågan/svaret till. Jag tolkade det som att man skulle svara för vilka n som gav svar till α+β≤|π|⇔-π≤α+β≤π och där gavs svaret n = 0, 1.
Ska man kanske istället tolka det som för vilka n man får 0≤α+β≤π, då en reell längd inte kan vara mindre än noll?
d) Vet jag inte vad jag ska göra på. Antingen får jag svar i stil med 1=1 (additionsformel för tan) eller så får jag felaktiga svar (additionsformel för sin, cos).
Standardfråga 1a: Har du ritat? Enhetscirkeln. Med hjälp av dem ser du vilken kvadrant vinkeln α+β skall ligga i, och därmed vilken av alla tänkbara vinklar som är den enda riktiga.
Behöver du mer hjälp, så lägg upp bilden av enhetscirkeln här och berätta vad det är du behöver hjälp med.
Det är helt rätt att lägga alla dessa frågor i samma tråd, eftersom de handlar om samma uppgift. /moderator
Eftersom arcsin är entydigt definierad så har α+β också ett entydigt definierat värde.
Hej!
Uppgift c. Du ska finna två tal A och B sådana att A<α+β<B och 0<B-A<π.
Om du ritar en standardtriangel så hjälper det antagligen dig:
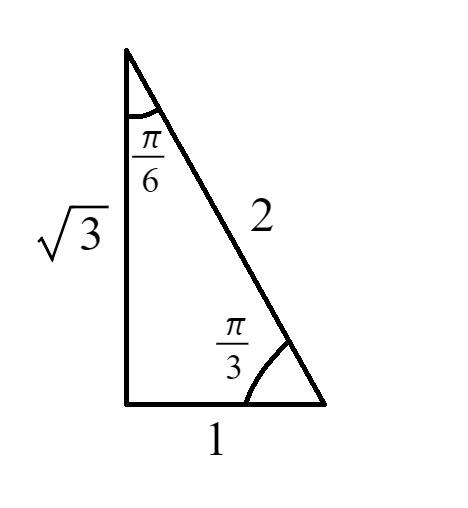
Följ nu Smaragdalenas råd och rita in de två alternativ du har i enhetscirkeln (den där kateterna är -1 och √3 eller den där kateterna är 1 och -√3). Bedöm sedan vilken av dem som är likvärdig med given information.
Ledning:
För att lösa uppgiften på detta vis ska du ha god koll på begrepp som värdemängd för de inversa trigonometriska funktionerna men det antar jag att du har? Exempelvis har vi att:
-π2≤arcsin(x)≤π2
Vilket ger att:
-π2≤α≤π2
Men, vi vet att x=1314>0 vilket ger att arcsin(x)>0 så α>0 osv.
Tack för alla tipsen!
Jag gjorde som ni föreslog och ritade enhetscirkeln med två möjliga vinklar 5π/6 samt -π/6.
Eftersom 0<α+β≤π/2 så är enbart 5π/6 en lösning, vilket är svaret :)
Pompan skrev:Tack för alla tipsen!
Jag gjorde som ni föreslog och ritade enhetscirkeln med två möjliga vinklar 5π/6 samt -π/6.
Eftersom 0<α+β≤π/2 så är enbart 5π/6 en lösning, vilket är svaret :)
Är alfa+beta både lika med 5pi/6 och mindre än pi/2?
Vänta lite, tror jag slarvade där? Intervallet är ju givet enligt c) som 0<α+β<π
Hade a+β≤π2 vore 5π6inte en lösning.
