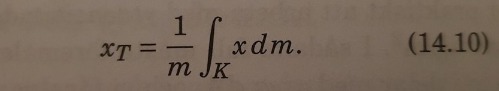Beräkning av masscentrum, y^t
En rak cirkulär kon med höjden 2m och radien 1m har spetsen nedåt och är fylld med vätska. I ett plant snitt parallellt med konens bottenyta och på avståndet x m från konens spets är vätskans densitet (10-x^2) kg/m^3. Bestäm vätskans masscentrum.
Massan har jag redan räknat, det är 76*pi/15. Jag har också fått fram x-koordinaten den är 55/38. Men jag vet inte hur jag får y^t, alltså y-koordinaten. 
Det är väl så här som konen nu ska se ut? Jag använder formeln för rotation kring (vanligtvis) y-axeln med höjden (2-2y) och får dV = (2-2y)*2*pi*y*dy.
sedan för att beräkna dm omvandlar jag ro som ges av 10-x^2 till (10-y)^1/2 (känns fel men jag kan väl inte räkna med både x och y?). Så jag får y^t =
vilket känns väldigt rörigt och fel.
Tipsen säger att dm ska vara en tunn skiva med radien y så att dm = ro*pi*y^2 men jag förstår inte det jag kan väl inte ta skivor för den roterar ju genom x-axeln (den lodrätta axeln).
Svaret ska vara 55/38 l.e från konens spets på konens symmetriaxel. Men jag förstår inte hur det gick till.
det e ok jag koppla nu, jag behöver inte beräkna y^t för densiteten är konstant i varje skiva jag gjorde vid beräkningen av x^t vilket betyder tyngdpunkten måste ligga på konens symmetriaxel.
Bra att det gick bra, men vad menar du med y^t?
Laguna skrev:Bra att det gick bra, men vad menar du med y^t?
Jag har skrivit det lite krångligt, den ska stå för y-koordinaten av tyngpunktskoordinaten. Formeln ser ut såhär i boken (fast skriven med x istället för y):