Beräkning av punkter på en ritning
För att lära mig hur man ska tänka går jag i vissa fall bakvägen, med hjälp av facit, som här bifogas uppgiften. I det här fallet kan jag komma fram till samma svar som facit, vad gäller 1, 2, 5 och 6. Punkten 3:s koordinater ställer jag mig helt frågande till, samt 4b:s koordinater.
Vad jag ändå inte begriper är hur jag utan facit ska kunna få fram cos vinkeln mellan punkterna 1 och 2b. Jag gjorde en triangel med hypotenusan R20 till höger, som även kan ses på ritningen. Vid ritningens mittlinje har jag en rät vinkel upptill, medan ett hörn i vinkeln är där både 2a och 6a finns.
Jag fick fram y-värdet 3,33 genom att i facit utläsa skillnaden mellan 2 a:s och 2 b:s y-lägen (höjdlägen) = 3,33. Därefter har jag kommit fram till att 3,33/20 ger cos vinkeln 80,42 grader. Då finner jag även x-värdet för 2b.
Man bör ju kunna finna koordinaterna utan att ha tillgång till facit och gå bakvägen. Matematiker kan säkert hur man ska få fram vinklarna, eller något annat som gör att man kan lösa liknande uppgifter när man inte har facit. Tack på förhand!
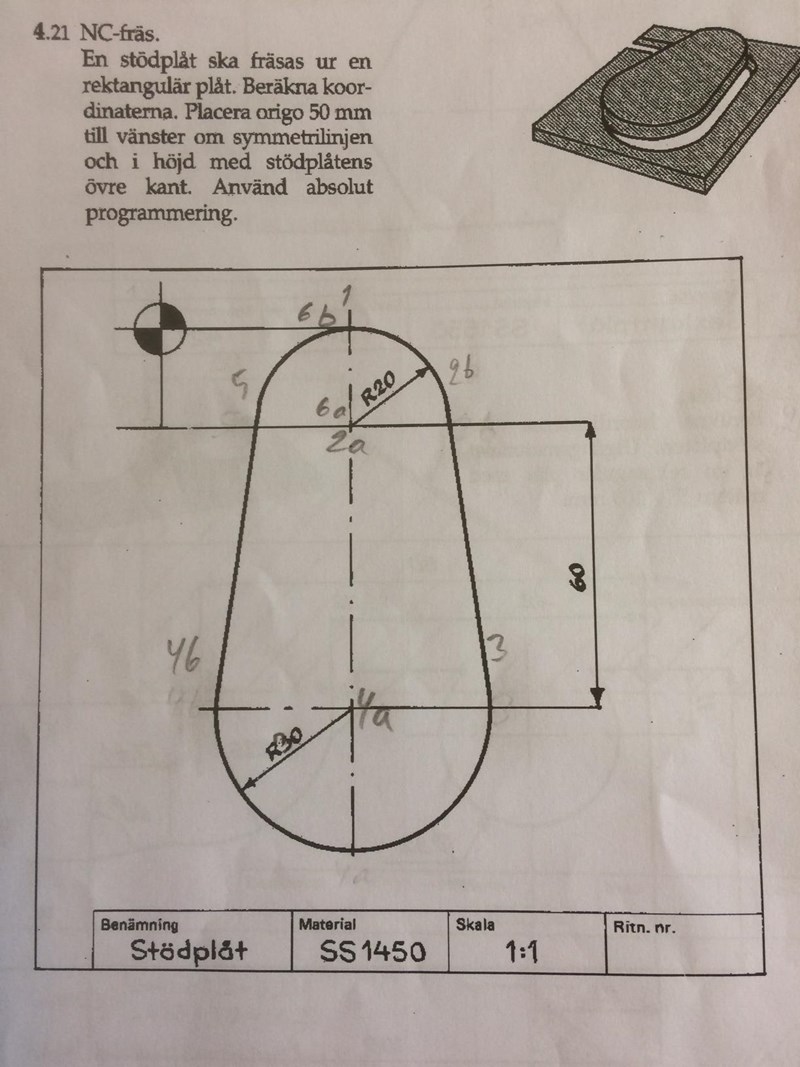
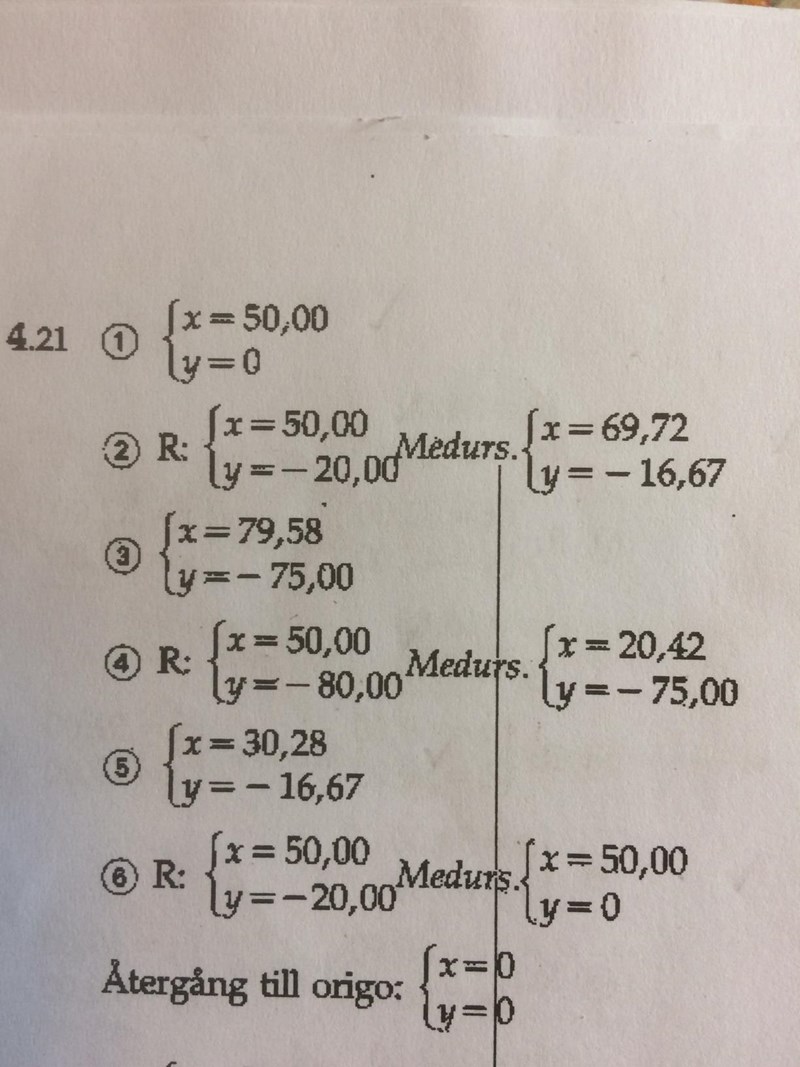
Jag gör en triangel med hypotenusan 30, som även innebär R30 nertill i ritningen men radien i motsatt riktning uppåt mot höger. Hypotenusan går mellan 4a och 3. Enligt facit är höjdskillnaden y så mycket som 5 mm mellan 4a och 3. Det finns en rät vinkel i triangeln lodrätt under punkten 3, emot cirkelns mittlinje. Vinkeln vid 4a är 9,60 grader för att jag ska kunna få fram X-värde för 3 (X = 50 + katet X 29,58 = 79,58) respektive X-värde för 4b (X = 50 - katet X 29,58 = 20,42). Det här borde jag kunna få fram utan att först se i facit, men hur?
Jag tar bara högra sidan:
1. Rita 2 cirklar. En med radien 20 med mittpunkt i origo. En med radien 30 med mittpunkt (0,-60)
lämna rätt mycket plats ovanför cirklarna typ till y=130
2. Dra en linje som tangerar bägge linjerna och korsar y-axlen (vid ca y=120)
3. kalla skärningspunkten mellan tangenten och y-axlen för P och vinkeln för a
4. Du kan nu skriva 2 uttryck:
sin a = 20/P och
sin a = 30/(P+60)
sätt uttrycken lika med varandra (det är ju samma a)
20/P = 30/(P+60)
Detta ger at P=120 skärningspunkten mellan y-axeln och tangentenär alltså (0,120)
För att få fram vinkeln:
sin a=20/120=1/6 och motsvarande för stora cirkeln:
sin a=30/(120+60)=30/180=1/6 (såklart skall det bli samma)
detta ger dig en toppvinkel a på ca 9,4623
och vinkeln mellan y-axlen och vardera radie blir ca 80,5376
(det blir ju såklart samma vinkel)
Edit: du skulle kunna använda cosinus istället och ta fram rätt vinkeln direkt ....


